CP walks into the office.
Cushing: Christian, look at this. I’ve asked Wolfram Alpha to plot a quadratic going through three squares.
CP: That’s odd. Could that work? There’s a plus and a minus, so maybe if you don’t think about it too hard it does work on those points.
Cushing: Let’s try smaller squares. $(1,1)$, $(2,4)$, $(3,9)$.
CP: Well, that doesn’t work. Maybe it’s floating-point error – you can’t write $3$ in binary easily.
Cushing: OK, $(0,0)$, $(1,1)$, $(2,4)$.
CP: Oh my!
…
CP: At least the powers of ten are smaller.
Cushing: No, they’re bigger.
CP: Mathematicians, David! Smaller!
Cushing: Oh yes. Hm. Does it give the same numbers for the same input?
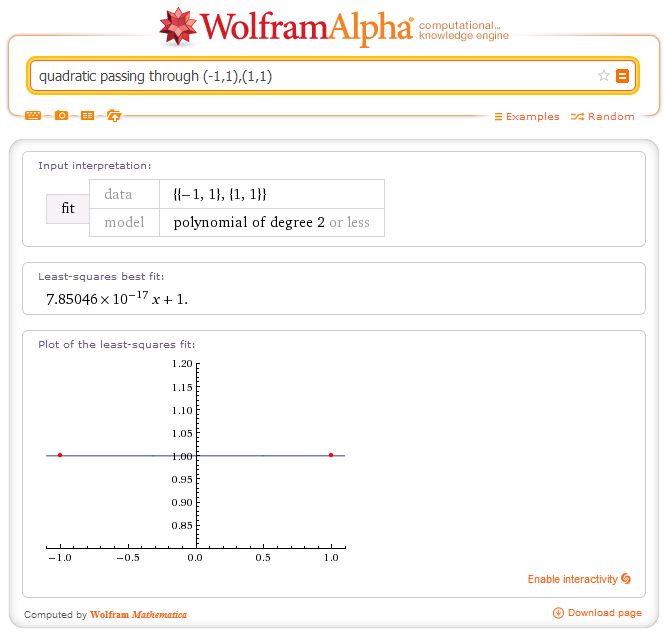
CP: I’m both encouraged and disappointed. You could try $(-1,1)$, $(0,0)$, $(1,1)$.
Cushing: I didn’t think of that!
CP: That definitely definitely doesn’t work.
Cushing: It’s $\pi \times 10^{-16}$. Who knew?
CP: Not me.
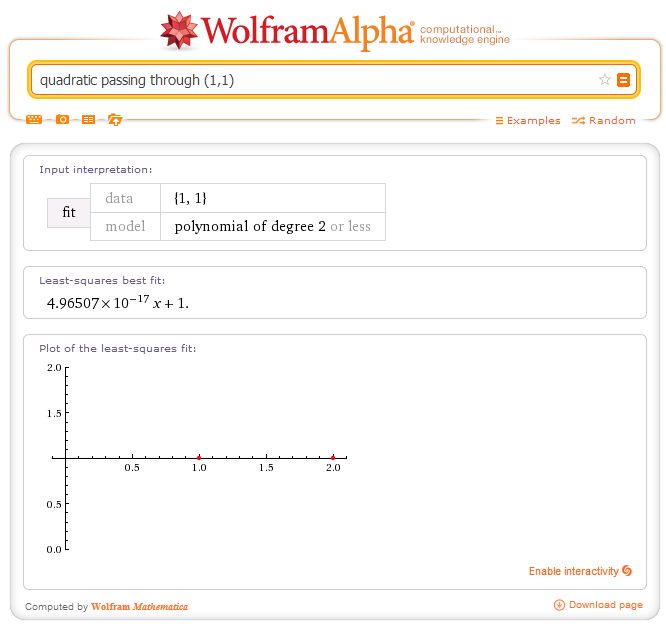
Cushing: Let’s try two points.
CP: That doesn’t even look right on the graph!
Cushing: …
CP: !!!
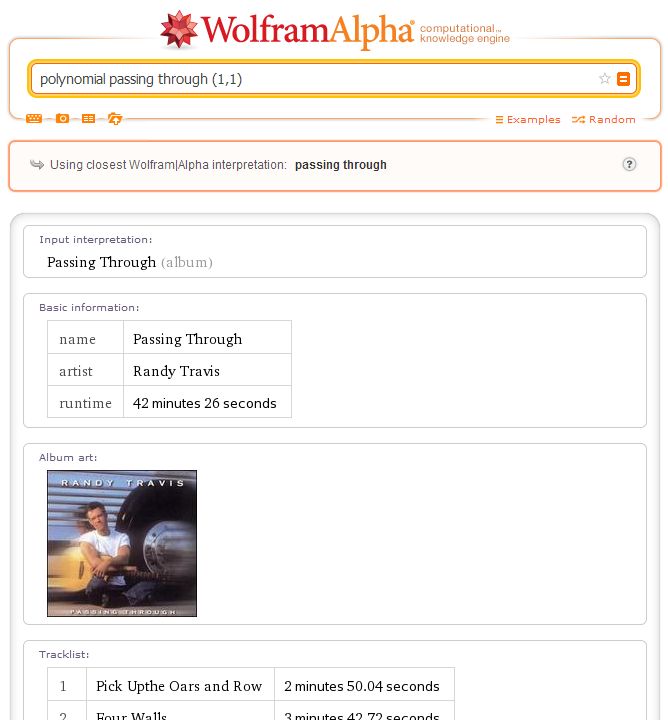
Cushing: Maybe I’m wording it wrong.
CP: And there you go. Finally, the information we were looking for.
Cushing: Actually, the number of polynomials that pass through a particular point has measure zero, so we were asking a lot.
CP: You’re saying that it’s correct that we never got a polynomial that fits?
Cushing: Well, you’ve got a zero probability of picking one that works, so, yes.
Postscript
As of the 6th of February 2014, it looks like someone at Wolfram has noticed this oddity and fixed it. All of the searches we do above now return what you’d expect.
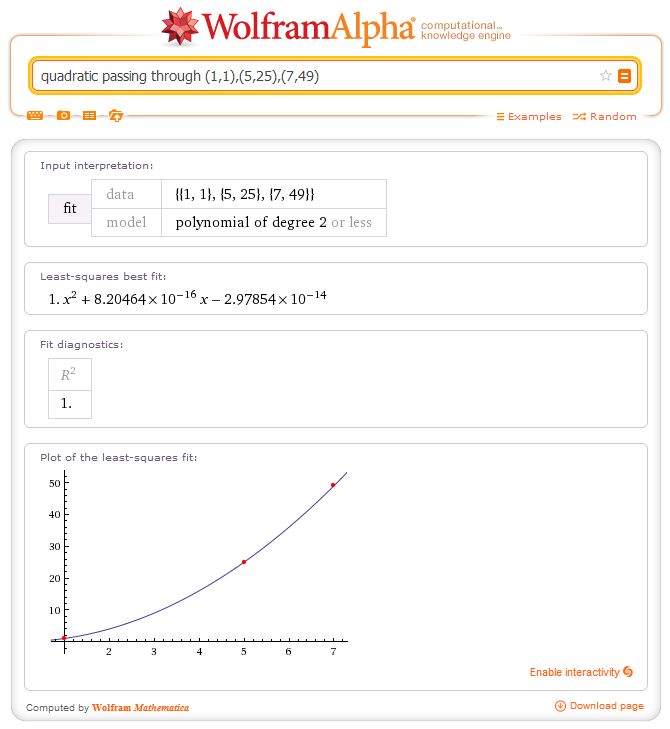
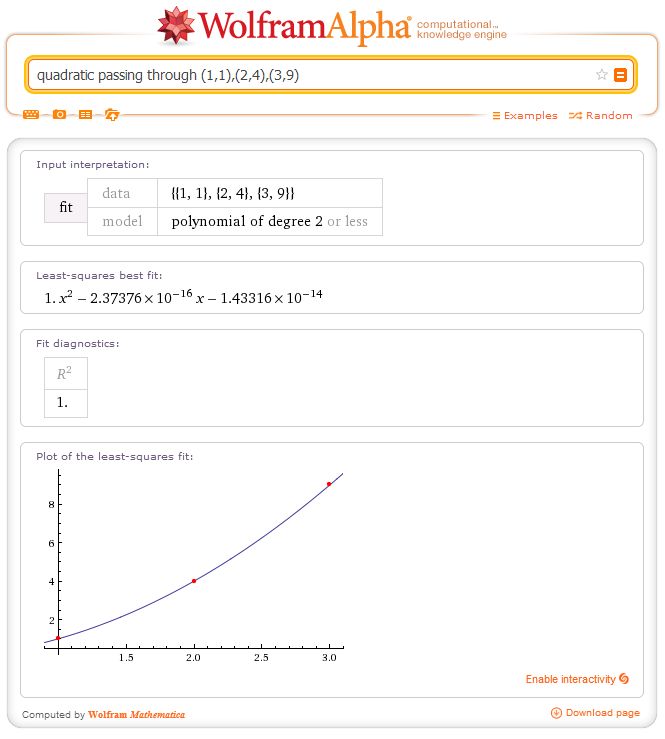
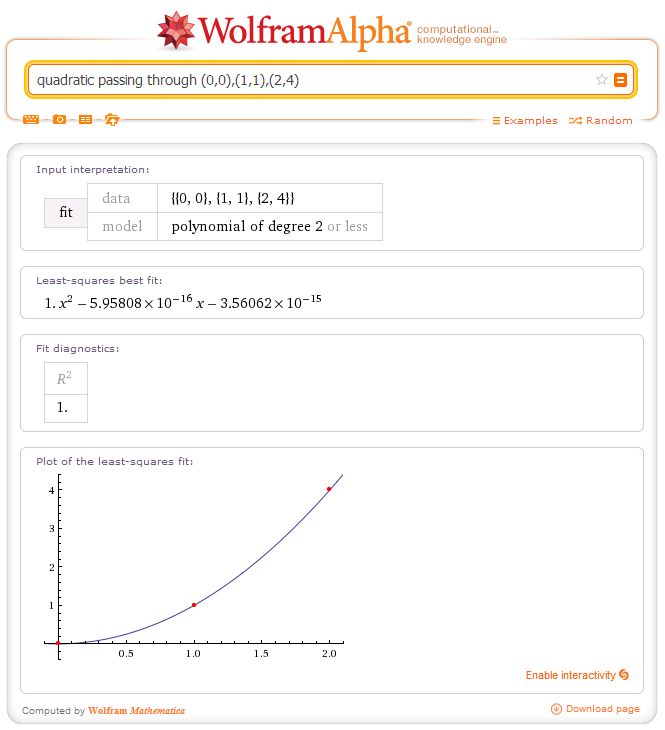
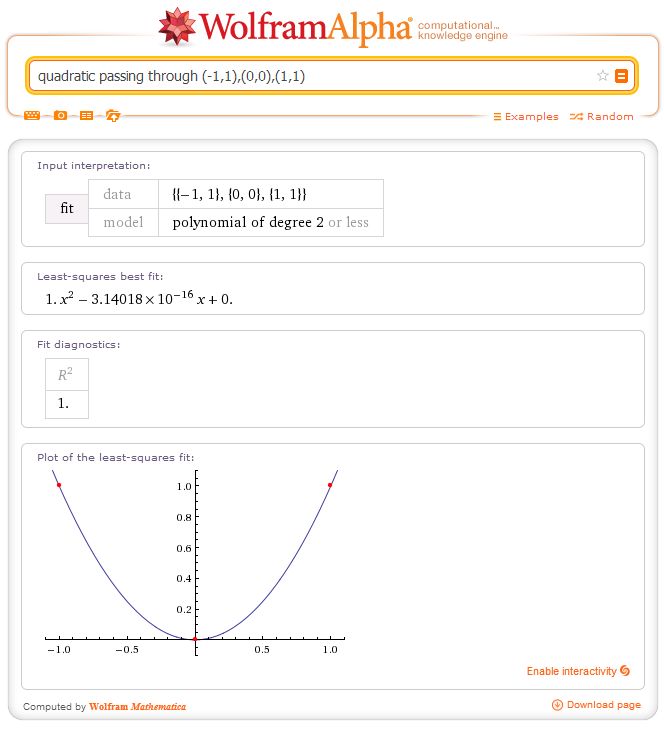
Just saying that those equations it supplied are perfectly reasonable in terms of accuracy. think about it, this is the equation supplied in the first one: $x^2 + 8.20464\times10^{-16}x – 2.97854\times10^{-14}$
This value here: $8.20464\times10^{-16}$ is so close to $0$ it almost has $0$ visible effect on the graph so if we set both of those values to 0 our equation will simply be $x^2$ which is what the graph will be if worked out correctly. this is the same for all the other graphs, all the values are so small they are making almost no visible effect.
So why does it come up with these values? well I’d say its mainly due to rounding issues in the coding. I would say that in Wolfram Alpha’s code it would assume that all values for $a, b, c$ in the equation $ax^{2}+bx+c$ will be irrational as would be the case for almost all values told to fit to. It would then use some algorithm to calculate it and then round it off to the first 6 digits. Why would it not just accept 0? well if it assumes that all values are irrational then it won’t put 0 as it isn’t irrational instead it will use a close estimate which seems to vary depending on the points supplied.
Yes, we understood what’s going on – it’s using an algorithm which assumes the input points aren’t on the line of best fit, and the extra terms arise from floating point errors – but it tickled us, hence the post.
A few people on Reddit pointed out (less politely) that Alpha will do the right thing if you ask it to ‘interpolate {points}’ instead.
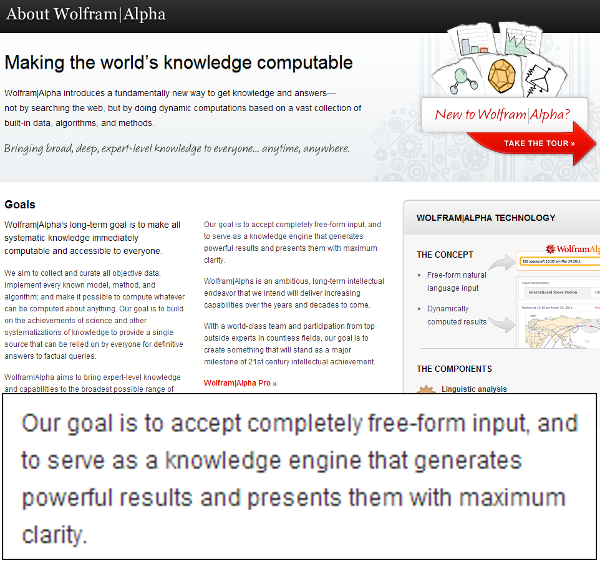
But the reason we included the grandiose blurb at the end of the post is to point out that Wolfram Alpha claims to take natural language input. We didn’t say “run algorithm X on these data points”, we asked it to find a quadratic passing through them. If the system was understanding queries in the way they claim it is, it’d notice that $x^2$ is the obvious solution.
Seems that Alpha understands “parabola” better than “quadratic”. Got the exact equation when I inputted it that way. Very strange.