The Online Encyclopedia of Integer Sequences contains over 200,000 sequences. It contains classics, curios, thousands of derivatives entered purely for completeness’s sake, short sequences whose completion would be a huge mathematical achievement, and some entries which are just downright silly.

For a lark, David and I have decided to review some of the Encyclopedia’s sequences. We’re rating sequences on four axes: Novelty, Aesthetics, Explicability and Completeness.

CP: It’s Neil Sloane’s 75th birthday today! As a special birthday gift to him, we’re going to review some integer sequences.

DC: His birthday is 10/10, that’s pretty cool.

CP: <some quick oeis> there’s a sequence with his birthdate in it! A214742 contains 10,10,39.

DC: We can’t review that. It’s terrible.

CP: I put it to you that you have just reviewed it.

DC: Shut up.

CP: Anyway, I’ve got some birthday sequences to look at.

DC: About cake?

CP: No.

A050255
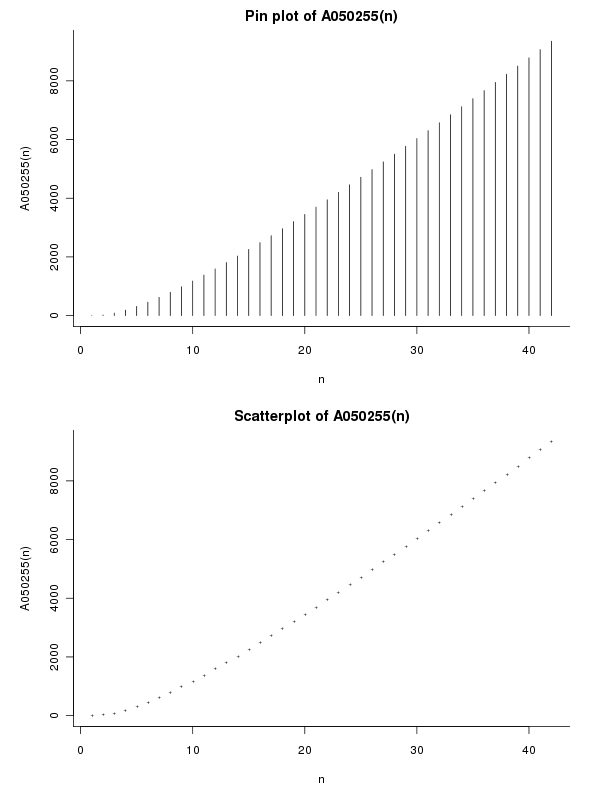
Diaconis-Mosteller approximation to the Birthday problem function.

1, 23, 88, 187, 313, 459, 622, 797, 983, 1179, 1382, 1592, 1809, 2031, 2257, 2489, 2724, 2963, 3205, 3450, 3698, 3949, 4203, 4459, 4717, 4977, 5239, 5503, 5768, 6036, 6305, 6575, 6847, 7121, 7395, 7671, 7948, 8227, 8506, 8787, 9068, 9351

DC: I like Diaconis. That’s my first thought. Don’t know who Mosteller is though. 3/5.

CP: Mosteller is/was a dude and/or ladydude.

DC: Will you explain the sequence please?

CP: I’ll try, but the OEIS entry doesn’t give us much to go on. It refers to a paper called “Methods of studying coincidences“. Which is a coincidence, because I’ve got that very paper right here. As far as I can tell, the approximation producing this sequence is their equation 7.5, i.e.

\[ Ne^{-N/ck}/(1 – N/c(k+1))^{1/k} = \left[ c^{k-1}k! \log_e \left( \frac{1}{1-p} \right) \right]^{1/k} \]

CP: Whew. Feel like checking that’s right?

DC: <firm nods of the head>

The real DC: SHAKES! SHAKES OF THE HEAD!

CP: OK, let’s get on with reviewing this in our four categories, which are well-defined and we understand completely.

Explicability

DC: Zero. I still don’t know what they’re on about.

CP: It’s an approximation to the number of people you need to have in the same room to have a 50% chance that $N$ of them will share a birthday. Some would say it’s more hassle to work out this approximation than the real value.

DC: Can I look at this in graph form? I’m getting bored.

CP: OK…

CP: Well, it’s exponential.

DC: It’s linear!

CP: Do I need to draw a tangent on the bottom bit? Or maybe point you to the equation of the function, which contains an exponential.

DC: It’s a log to an exponential. It’s linear.

CP: Yeah, but you solve that for $N$.

DC: I think it’s linear. I say we get the random number generator out and move on.

CP: OK..

\[ \frac{6}{5} \text{ (generated by fair dice roll)} \]

Novelty

CP: Jeez I am so sick of the birthday problem! Zero. Minus zero!

DC: Agreed.

\[ – \frac{0}{5} \]

DC: No, minus one. You said minus zero factorial.

\[ – \frac{1}{5} \]

Aesthetics

CP: The graph is pretty but the equation is yuckly. I’m not sure.

DC: $\frac{1}{5}.$

CP: Won’t argue with that.

\[ \frac{1}{5} \]

Completeness

DC: It’s an approximation. It can’t be complete.

CP: And apart from that, the OEIS entry is woefully lacking in detail. Not even a PARI formula, which is like the minimal possible usefulness because nobody uses PARI.

DC: Sloane should be ashamed of himself. I’ll let him off this once since it’s his birthday.

CP: Actually, it’s Eric Weisstein who’s to blame. Him with his own world of physics.

DC: When’s his birthday? I say we don’t review a sequence on his birthday, just to teach him.

CP: I can almost guarantee that’ll happen. Anyway, we need a score. There are a good number of elements in the OEIS entry.

DC: One of them’s palindromic as well. Did you see it?

CP: Four of them! In the first eight terms! This is a palindrome goldmine!

DC: But it’s got hardly any of the possible palindromes. $\frac{1}{5}$.

CP: This isn’t the “how many palindromes has it got” category. Because you’re not taking this seriously, I’m going to remove your voting rights for this category. So I say the score is:

\[ \frac{212}{515} \]

How many palindromes has it got

CP: Four. We just said so.

DC: Which isn’t many.

\[ \frac{1}{5} \]

DC: Let’s add up the scores!

Total score

DC: I say we get Wolfram Alpha to do it. It’s very complicated today.

\[ \frac{6}{5} + – \frac{1}{5} + \frac{1}{5} + \frac{212}{515} + \frac{1}{5} = \frac{933}{515} \]

DC: We need to divide by five.

CP: Yeah, we normally miss that part out in our calculations.

\[ \frac{933}{2575} \approx 0.36 \]

CP: Not a great score. In fact, that’s around about what I would’ve given it if we hadn’t been stupid in all five (out of four) categories. The system works!

DC: Woohoo! Now let’s bake Sloane a cake that he can’t eat.

CP: He actually nominated me as his cake-eating proxy in case of such circumstances as these.

DC: Are you sure, because I’m going to bake it.

CP: I was lying.