A conversation about mathematics inspired by a Battenberg cake. Presented by Katie Steckles and Peter Rowlett.
Podcast: Play in new window | Download
Subscribe: RSS | List of episodes
Mathematical Objects: Battenberg cake
You're reading: Posts Tagged: cake
Geogebra to Cake in Five Steps
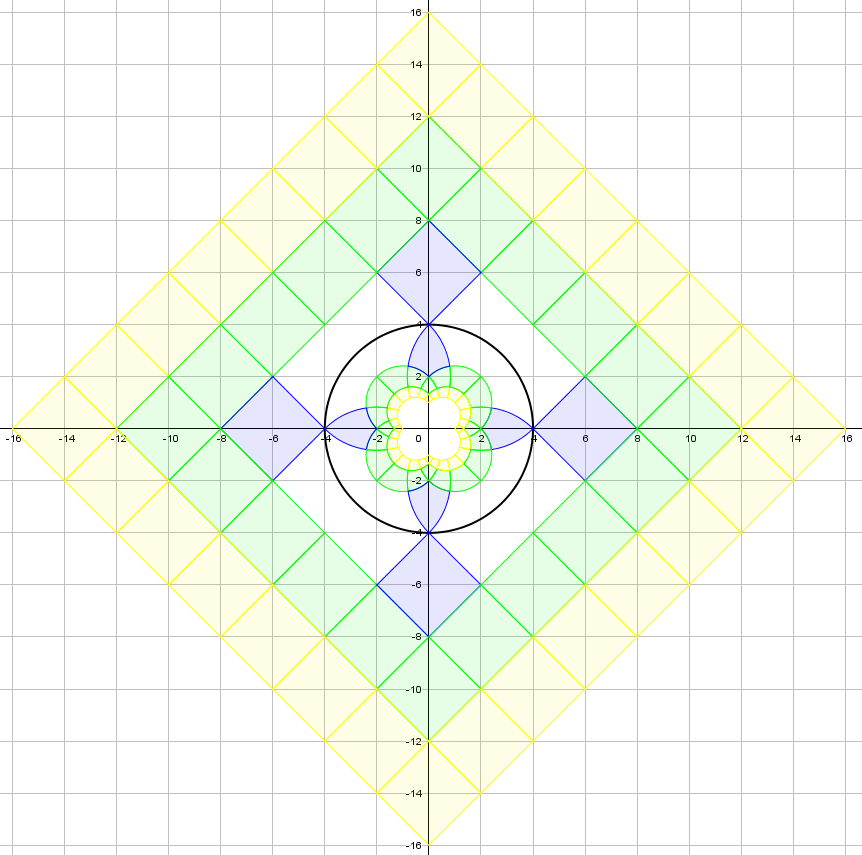
In the Aperiodical’s Big Internet Math-Off 2019, Becky Warren posted an entry about Geogebra’s ‘reflect object in circle’ tool (it’s the second article in the post). I enjoyed playing with the tool and, after making a few colourful designs, it occurred to me that one of them would make a great cake for the MathsJam bake-off. It would only work if the curves were accurate; sadly this would be beyond my drawing abilities, and definitely beyond my piping abilities. But with some help from 3D printing I thought I might be able to manage it.
Here are the steps I used to transfer the design to a cake.
Integer Sequence Review – Sloane’s birthday edition!
The Online Encyclopedia of Integer Sequences contains over 200,000 sequences. It contains classics, curios, thousands of derivatives entered purely for completeness’s sake, short sequences whose completion would be a huge mathematical achievement, and some entries which are just downright silly.
For a lark, David and I have decided to review some of the Encyclopedia’s sequences. We’re rating sequences on four axes: Novelty, Aesthetics, Explicability and Completeness.
CP: It’s Neil Sloane’s 75th birthday today! As a special birthday gift to him, we’re going to review some integer sequences.
DC: His birthday is 10/10, that’s pretty cool.
CP: <some quick oeis> there’s a sequence with his birthdate in it! A214742 contains 10,10,39.
DC: We can’t review that. It’s terrible.
CP: I put it to you that you have just reviewed it.
DC: Shut up.
CP: Anyway, I’ve got some birthday sequences to look at.
DC: About cake?
CP: No.
A050255
Diaconis-Mosteller approximation to the Birthday problem function.1, 23, 88, 187, 313, 459, 622, 797, 983, 1179, 1382, 1592, 1809, 2031, 2257, 2489, 2724, 2963, 3205, 3450, 3698, 3949, 4203, 4459, 4717, 4977, 5239, 5503, 5768, 6036, 6305, 6575, 6847, 7121, 7395, 7671, 7948, 8227, 8506, 8787, 9068, 9351