This is the twelfth match in our group stage: from Group 4, it’s Kyle D Evans up against Becky Warren. The pitches are below, and at the end of this post there’s a poll where you can vote for your favourite bit of maths.
Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!
Kyle D Evans – T-shirts of Hanoi

Kyle D Evans is an award-winning maths communicator, musical comedian, teacher and general jack of all mathematical trades. He’s @kyledevans on Twitter.
Have you ever had a play with one of these things? When I was a child they used to annoy the hell out of me, and it started a long fascination:

This game is called the Towers of Hanoi and it was invented in 1883 by Eduoard Lucas (making it just 2 years older than the world’s greatest football club.)
The rules are very simple, the discs must be moved from the left-hand peg to the right-hand peg, one disc at a time, using the middle peg whenever necessary, and never putting a larger disc onto a smaller one. Here is an online version where you can try for yourself, and here’s an animated representation of the perfect 4-disc solution:

One thing I always noticed as a child was that the difficulty seemed to increase hugely from three discs to four discs, when the total number of required moves went up from 7 to 15 (this may have something to do with the magical number seven, plus or minus two.)
What I needed to do was find a method – an algorithm to follow – that would allow me to approach the puzzle with a larger number of discs. Luckily I had a coloured Towers of Hanoi set, and an early intuition of one of the most important skills in mathematics: if a problem is too hard, make it easier and look for patterns.
Warning: the image below is not the most advanced piece of mathematics you’ll see in the Big Math-off 2019. It’s a visualisation of the perfect solution for a Towers of Hanoi set with one disc:

I hope you could follow that: one move on the red disc. Here’s two discs:
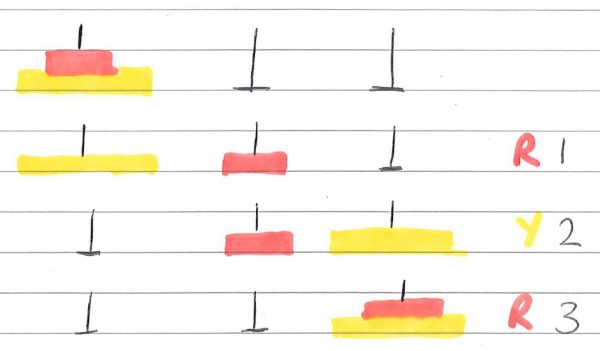
3 moves in total, the sequence being R, Y, R. Now three discs:
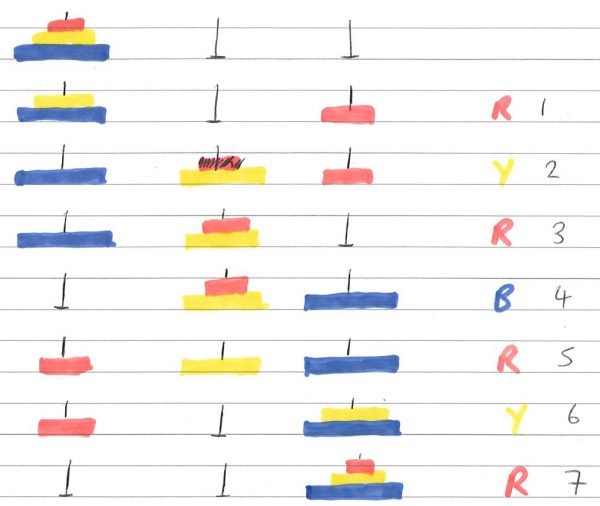
7 moves in total: R, Y, R, B, R, Y, R. And finally, that animated four disc solution again (my felt tips are running out):

15 moves in total: R, Y, R, B, R, Y, R, O, R, Y, R, B, R, Y, R. Now let’s look at all those sequences together:
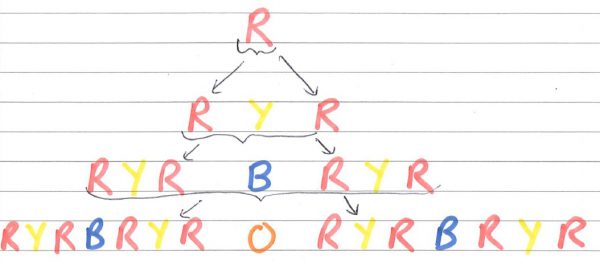
A beautiful symmetry emerges. The patterns of moves formed are recursive, so that the perfect strategy for any number of discs is always to perform the previous perfect strategy twice, with the new disc in between. It seems, therefore, that the number of moves required for any number of discs is twice the previous number of moves plus one. Let’s check:
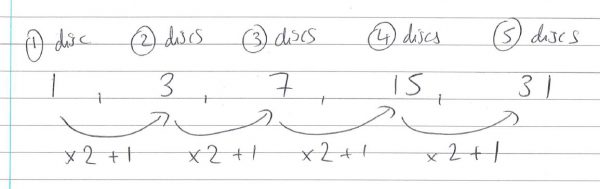
Great! Now as we require more and more moves, the ‘+1’ makes relatively less and less difference, meaning that every time we add a disc, it takes about twice as many moves to complete the game. The Wikipedia page for Towers of Hanoi features this incredible image from the Universum museum in Mexico City, of a Towers of Hanoi set with 32 discs.

I often ask audience members at my shows to guess how long it would take to complete this set, if you could move one disc per second. Guesses usually range from a few minutes to a few years. I’ll give you the pleasure of working it out for yourself, but it’s considerably longer that you’d manage in a lifetime. I’m fond of the idea of a family working through it across the generations, with a great-grandmother passing it on to her descendants after completing a few hundred thousand moves, but the thought of making an error and letting down your deceased ancestors is just too much to bear.
Luckily, there is a way to make sure you never go wrong. It feels like a bit of a cheat, so if you don’t want to see an algorithm for completing the Towers of Hanoi game, look away now:
| For an odd number of discs: | Make the legal move between A and C |
| Make the legal move between A and B | |
| Make the legal move between B and C | |
| Repeat | |
| For an even number of discs: | The same, but reverse the first two steps |
This is the algorithm that I ask my volunteers to use if they get stuck during one of my live party pieces, the T-SHIRTS OF HANOI! Below is a video of some volunteers playing the game at Cheltenham Science Festival this year. I’ve watched it back 5 or 6 times and I’m still not sure whether we make a mistake or not. But they gave it a good old go, and that, after all, is the most important thing in mathematics. If you want to check, there should be 31 moves and the sequence of t-shirt changes should be as below. Enjoy!

Becky Warren – Reflecting Circles

Becky Warren is a freelance maths educator and communicator. She loves neat mathematical puzzles, mathematical art and origami. Her occasionally updated blog is called Lines Curves Spirals. She’s @becky_k_warren on Twitter, where she loves joining in the #beingmathematical chat on Thursdays.
I discovered the “Reflect Object in Circle” tool on GeoGebra by accident.
Below you can explore what happens when you reflect a point, a ray, a line, or even some polygons in a circle.
What do you notice?
How does A’ move when you move A?
Where is A’ when A is at (1,1)?
Does the reflection of the ray act as you imagined?
Why does the curve always start from the origin?
What shape does the line make when it is reflected in the circle?
What shapes can you make with the reflections of the polygons?
What happens if you move the polygon inside the circle?
What shape would you expect a circle to make when reflected in a circle?
If you’re interested in a deeper look at the mathematics behind this tool there is some more explanation here.
In any case, I invite you to download GeoGebra, have a play around with the “Reflect Object in Circle” tool and share your creations with the hashtag #BigMathOff!
To start you off, here’s one I made earlier!

So, which bit of maths do you want to win? Vote now!
Match 12: Group 4 - Kyle D Evans vs Becky Warren
- Becky with circular reflections
- (52%, 100 Votes)
- Kyle with a t-shirt puzzle
- (48%, 93 Votes)
Total Voters: 193
This poll is closed.
The poll closes at 9am BST on the 13th. Whoever wins the most votes will win the match, and once the group stages are over, the number of wins will determine who goes through to the semi-final.
Come back tomorrow for our thirteenth match of the group stages, featuring Lucy Rycroft-Smith and Alaric Stephen. Or check out the announcement post for your follow-along wall chart!
Interesting how many fifth matches this tournament has. It must be a loop in time!