This week, Katie and Paul are blogging from the Heidelberg Laureate Forum – a week-long maths conference where current young researchers in maths and computer science can meet and hear talks by top-level prize-winning researchers. For more information about the HLF, visit the Heidelberg Laureate Forum website.

As part of the HLF, the Laureates are participating in press conferences throughout the week, and being bombarded with questions by well-meaning journalists and bloggers. Unlike most press conferences, where participants often have a specific topical thing they’re there to speak to the press about, the Laureates can be asked about any of their past projects, on any area of maths they’ve worked on, and many of them have a very long and illustrious career to speak of.

It can be difficult then, to be put on the spot by a taxing question, especially if you’re not expecting it. I’ve been surprising the topologists whose press conferences I’ve attended with a deceptively deep but simple question: What’s your favourite manifold?

This question has had mixed results – known Poincaré-botherer Stephen Smalewas unwilling to provide an answer, essentially because he loves all manifolds equally (he wouldn’t even narrow it down to one infinite family, although we know he probably really has a soft spot for the n-sphere, in the case n>5).

The best answer I’ve had so far came from algebraic topologist, Abel Prize winner and Fields Medalist Sir Michael Atiyah. After a moment’s thought, he stated that he definitely did have a favourite manifold, and that it’s a particular K3 surface he’s studied recently.

Wait, what’s a Manifold?

You may well be wondering what a manifold is – and to a topologist, it’s as fundamental as what a number or an equation is. A manifold is a surface which locally looks like ordinary Euclidean space – if you look close-up at a small part of the surface, it behaves normally. For example, if your manifold is 2-dimensional, this means that each small part of it looks like a flat piece of 2D surface, with coordinates in the usual way, and the distance between two points defined the way you’d expect.

A great example of a manifold is a sphere – it’s locally, in very small patches, pretty much a sensible surface you could put a coordinate system on. In fact, we very much do this, as the earth itself is a sphere, and yet we tend to think about it in small 2D patches which we represent as flat on maps, and measure distance in a straight line, even though we know that they join up in a more complicated way to cover the whole surface of the sphere.

Manifolds come in all different kinds – without holes in, like the sphere; with holes in, like a torus or donut shape. There even exist some 2D manifolds which can’t be realised in 3D space without intersecting themselves, like a Klein bottle or a real projective plane.

It’s thought that manifolds are especially useful because this property of being easy to understand in small local patches means we can apply knowledge of how, for example, functions behave on those simpler parts to understand the whole shape, even when the complete structure is much more complex.

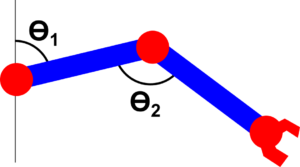They often crop up as the solution spaces to problems in physics or as graphs of functions. A nice example is the space of configurations a two-part robot arm could achieve – if it’s hinged at the shoulder and elbow, and each joint can be positioned at any angle from 0 to 360 degrees, the position of the arm is determined by a point on each of two circles; if you imagine extruding one of these circles along the length of the other, with the two circles running perpendicular to each other, you get a torus shape, and one single point on the surface of this torus corresponds to one possible configuration of the robotic arm.

What is a K3 surface?

K3 surfaces were first discovered by Ramanujan, back in the 1910s – while studying the diophantine equation a³ +b³ = c³ + d³, his writings reveal he anticipated the structures of K3 surfaces – although this work was never published. The name was coined in 1958 by André Weil, who named them after three revered algebraic geometers: Kummer, Kähler and Kodaria (and the mountain K2 in Kashmir).

A K3 surface is a type of Calabai-Yau manifold, which is a kind of manifold named after Eugenio Calabi (who first conjectured that they might exist) and Shing-Tung Yau. Calabai-Yau manifolds have many applications in theoretical physics, and it’s conjectured that the extra dimensions of space-time take the form of a Calabai-Yau manifold in 6 dimensions.

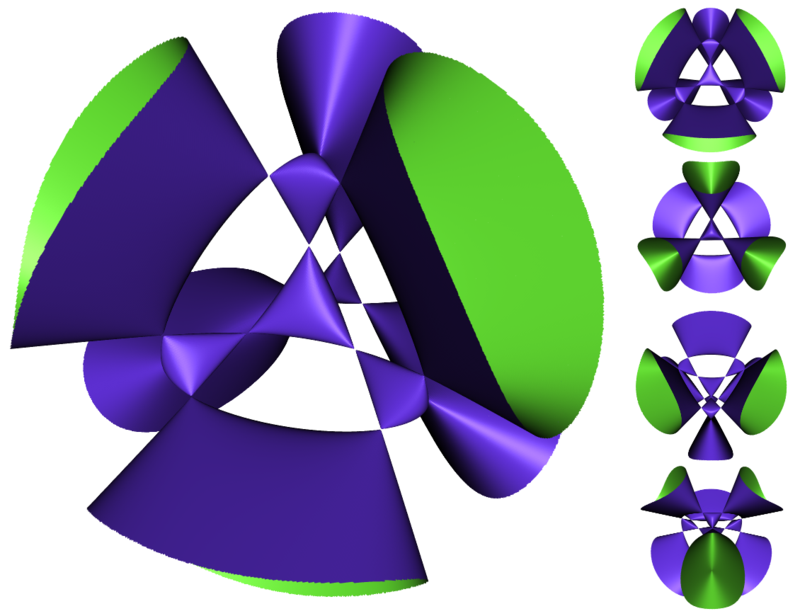
K3 surfaces are a particular subset of Calabai-Yau manifolds. They can often be found as the intersection or the product of other objects, and are closely related to elliptic curves, and to higher-dimensional analogues of the torus. The image below shows a Kummer surface, which is a type of K3 surface.

Image by Claudio Rocchini (CC-BY-SA, on Wikipedia)

Atiyah’s Favourite

The particular K3 surface Michael Atiyah specified as his favourite is one made as a product of two elliptic curves. He came across it as part of some work he did recently studying atoms and their isotopes, and using complex geometrical surfaces to model the shape of the atoms.

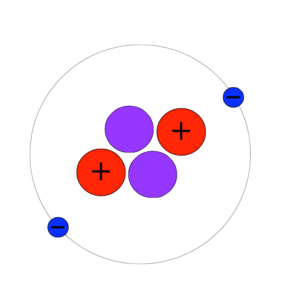
Helium-4 is a stable isotope of helium, meaning it’s a version of the helium atom with two neutrons, so (along with its two protons) it has a total mass of 4. Helium-4 is the most commonly occurring isotope, although Helium-3 also exists (having only one neutron).

The elliptic curve corresponding to the shape of Helium-4 is given by y² + x⁴ − 1 = 0, and it’s easy to see why this manifold has captured Atiyah’s imagination. Studying the topological properties of atoms, molecules and even larger biological structures such as DNA and proteins has been incredibly fruitful and in recent years has led to some interesting results.

What’s your favourite manifold?

More Information

The 1729 K3 Surface (ArXiV paper on Ramanujan’s work on K3 surfaces)
Geometric Models of Helium (PDF, ArXiV paper)