This week, Katie and Paul are blogging from the Heidelberg Laureate Forum – a week-long maths conference where current young researchers in maths and computer science can meet and hear talks by top-level prize-winning researchers. For more information about the HLF, visit the Heidelberg Laureate Forum website.
The view on the boat deck – plenty of young researchers to corner!
Having extensively covered the talks and press conferences of the Laureates so far, we thought it was time to talk to some of the Young Researchers at this year’s HLF about the work they’re doing.
We took the opportunity of the Wednesday afternoon boat trip – a captive audience – to ask the researchers to tell us a bit about what they’re working on. Since we’re mathematicians, we thought our best plan of attack was to present the researchers with a simple challenge:
“Tell us about a number, or sequence of numbers, you use in your research”
We found a selection of researchers prepared to explain their work, by sharing with us the numbers behind what they’re doing.
Reynolds Number – Alexandru Mihai
Alexandru Mihai is studying flows in fluid dynamics – patterns of movement within liquids and gases, which can be modelled using differential equations relating properties of the fluid, such as temperature, pressure and viscosity.
The Reynolds Number is used to help predict flow patterns in different fluid flow situations. Initially discovered in 1851, the concept was popularised by fluid dynamics innovator Osborne Reynolds, and named after him in 1908.
The Reynolds number of a situation can be used to predict when the flow is about to change from a smooth to a turbulent type of motion. This is useful in designing aircraft, and modelling weather patterns. Alexandru mentioned it’s particularly useful because it can be applied to similar situations at different scale levels – so you can study a scale model of a plane in a wind tunnel, and apply your conclusions to a full-size plane.
Catalan Numbers – Pavel Avdeev
The Catalan Numbers crop up in lots of different ‘counting’ problems, and are the only sequence we were given that has an entry in the Online Encyclopedia of Integer Sequences.
One way to think about them is that the nth Catalan number gives you the number of ways to bracket a statement with n+1 terms. So for example, 1-2-3-4 could be bracketed to give you (1-2)-(3-4), 1-(2-(3-4)), 1-((2-3)-4), (1-(2-3))-4, or ((1-2)-3)-4): so the third Catalan number is 5. The numbers grow reasonably quickly: the sequence begins 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012…
Pavel uses these numbers in his graph-theoretic research in bioinformatics to study the structure of DNA, and ancestral genome reconstruction.
randn – Mabel Rajendran
Mabel’s research is into the controllability of stochastic differential equations, ie, equations that incorporate some random ‘noise’. Controllability is concerned with how a function’s outputs can be controlled by manipulating its state.
The numbers Mabel chose to represent her research are the random ones that the Matlab function ‘randn’ provides. This function generates random numbers drawn from a standard normal distribution. For those of you who want something concrete, here is a sample acquired from the equivalent function in a different software package (spot the massive outlier): -1.0261, -0.60365, 1.0681, -0.68539, -2.4482, -0.62760.
#P-complete numbers – Matthew Fahrback
Matthew studies approximation algorithms, and he told us about the counting problems he’s studying. Counting problems are questions like, if we take a given set of integers, how many subsets can we find which add up to zero? This type of problem is computationally difficult, and falls into a class called #P-complete (sharp-P complete). The answers to such problems are the numbers Matthew is trying to find.
These are more difficult than the better known class of NP-complete problems, and the particular problems Matthew is working on include computing the permanent of a matrix. This is a property of a matrix very similar to the determinant but much more difficult to compute in general. One of this year’s Laureates, Leslie Valiant, proved in 1979 that this problem is #P-complete.
p14, for p an odd prime – Saul Freedman
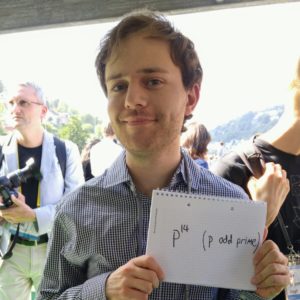Saul Freedman is a master’s student doing research in group theory. He’s constructing p-groups – groups whose size is a power of a prime number – related to certain exceptional groups of Lie type.
He wanted to tell us about one (well, one infinite family) in particular, of size p14 for p an odd prime, related to the group G2(p). So that’s 4,782,969 elements in the smallest case. His work involves constructing these groups and studying the types of transformations you can apply to them preserving the group structure.
ħ – Eric Stachura
In mathematical physics, ħ (‘h-bar’) is known as the reduced Planck constant, or Dirac constant and is given by the Planck constant h, divided by 2π. It can be used to calculate the energy and the linear momentum of a photon, and is part of the Schrödinger Equation in quantum mechanics.
Eric is studying the mathematical foundations of electronic structure theory, and the solvability of time-dependent Schrödinger equations.