I made a silly joke, and it made me think.
You may be aware that our own Christian Lawson-Perfect is running the Big Internet Math-Off here at the Aperiodical, a single-elimination tournament with sixteen competitors. I was knocked out in round one by the brilliant Alison Kiddle. I joked that if Alison went on to win, then I’d be joint second.
Much as I like and respect @ch_nira, I’ll be rooting for @ajk_44. If she goes on to win the #BigMathOff final and is crowned The World’s Most Interesting Mathematician, then I’m joint-second, right? https://t.co/8Jt37gHFif
— Peter Rowlett (@peterrowlett) July 10, 2018
I’ve been mulling this over and I felt there was something there in thinking about the placement of the non-winners in such a tournament, so I had a play.
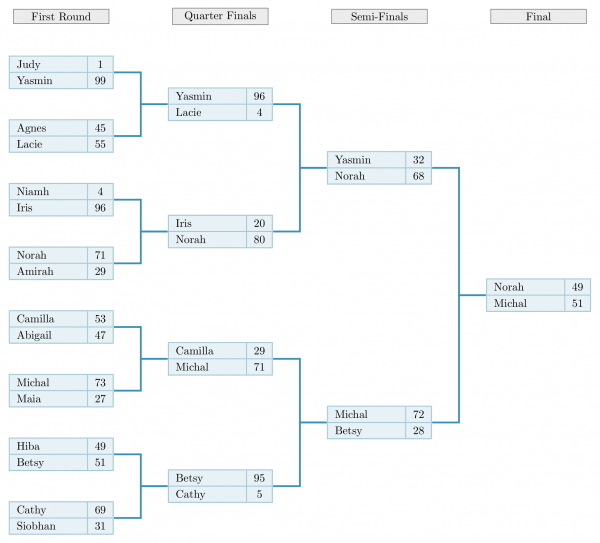
I started by doing the only sensible thing: I used an online random name generator to generate sixteen names and arranged them into eight first-round matches. Lacking an actual competition and with the Big Internet Math-Off in recent memory, I decided each match by generating a random number $0$-$100$ for one opponent and taking $100$ minus this for the other. Think of it, if you like, as percentage of a public vote. Thankfully, there were no draws, so I didn’t have to invent a tiebreaker rule.
Here’s the outcome, written up using this lovely LaTeX tournament code example.
Clearly, Michal wins, by winning the final. But who came second? Norah lost the final, so clearly has a claim to being second. She won one fewer match than did the winner.
But what about Betsy? Michal beat Betsy, so if we choose to believe the fiction of the tournament, Betsy is worse (at being assigned a random number $>50$) than Michal. But is she better or worse that Norah? Think about it. I’d say we don’t know, because this hasn’t been tested. We know Michal is better than Betsy, and Michal is better than Norah, but whether Betsy is better or worse than Norah is untested. All we can do, therefore, is award them joint second place. They both lost one match, to Michal, and they didn’t play each other.
But there are a bunch of other people who also lost only one match to Michal and haven’t played each other. If they hadn’t been knocked out, perhaps they could have gone on to win, or at least prove themselves better than one of our second-place candidates. So perhaps they are all joint second. The people Michal knocked out are: Norah, Betsy, Camilla and Maia.
By the same logic, if you were knocked out by a second-place competitor, you might have a claim to being joint third. As Michal beat Norah and Norah beat Yasmin, there’s a clear ordering here that puts Yasmin third. But Siobhan, who was beaten by joint-second-place Betsy, hasn’t played Yasmin, so I don’t think we can reasonably say Yasmin is better (at being assigned a random number $>50$) than Siobhan. The people beaten by a second-place competitor are: Yasmin, Iris and Amirah (knocked out by Norah), Cathy and Hiba (knocked out by Betsy) and Abigail (knocked out by Camilla).
Who was knocked out by a third-place competitor? Lacie and Judy (knocked out by Yasmin), Niamh (knocked out by Iris) and Siobhan (knocked out by Cathy). By the same logic, these are joint fourth place.
There is now only one competitor not placed: Agnes, who was knocked out by Lacie. An argument could be constructed to put her as the only competitor in fifth place.
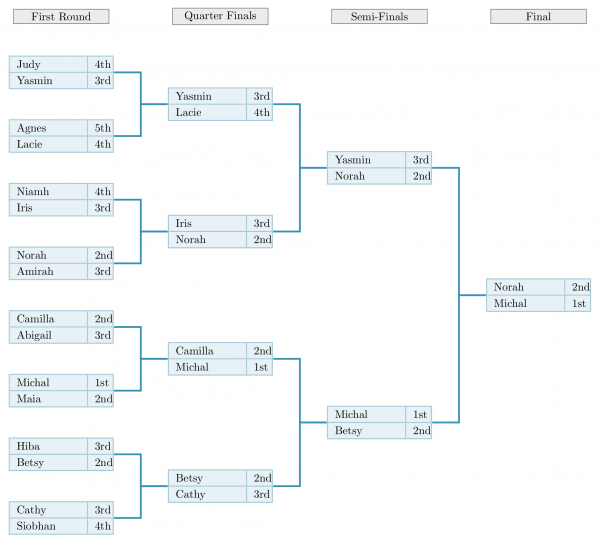
Here’s a diagram showing the tournament with these placements.
So in the final, we have two competitors: one in first place, one in second.
In the semi-finals, four: one first, two second and one third. That is, the two from the final are there in their original positions, plus they each knock out one competitor who is, therefore, placed one less than them.
In the quarter-finals: one first, three second, three third and one fourth.
In the first round: one first, four second, six third, four fourth and one fifth.
| Round | 1st | 2nd | 3rd | 4th | 5th |
|---|---|---|---|---|---|
| Final | 1 | 1 | 0 | 0 | 0 |
| Semi | 1 | 2 | 1 | 0 | 0 |
| Quarter | 1 | 3 | 3 | 1 | 0 |
| 1st | 1 | 4 | 6 | 4 | 1 |
Do we recognise these numbers? Labelling from the final backwards, at each stage we keep the competitors from the stage that happens after it in their places and add as many again that they knocked out, each one place below them. So, e.g., the number of second place competitors in the semi-final is the sum of the number of first and second place competitors in the final. In general, the number in column $m$ in row $n$ is made from the number who were in column $m$ in row $n-1$ plus the number in column $m-1$ in row $n-1$. We are making Pascal’s triangle.
I don’t think about single-elimination tournaments very much (I didn’t know the term until very recently), probably because I have little-to-no interest in sport. Is this result obvious to everyone? I appreciate it’s not the most practical way to look at a tournament — I’m not sure that anyone would seriously buy my argument that someone who rocked up in round one and won nothing, but happened to be playing the eventual winner, deserves joint second-place with the person who won three matches to be knocked out in the final. But as a bit of fun with logic, I thought it was quite nice.
Sadly, Alison was knocked out in the second round by Nira Chamberlain, so, depending on Nira’s performance in later rounds, the best I can hope for is joint-third place, and I might yet be fifth.

The words “partial order” don’t appear once in this post!