Here’s the seventh match in Round 1 of The Big Internet Math-Off. Today, we’re pitting James Propp against Zoe Griffiths.

Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!

James Propp – The mystery of the vanishing rope trick

James Propp is a professor at University of Massachusetts Lowell and author of the Mathematical Enchantments blog. You can find him on Twitter at @jimpropp.

Have you ever done something impossible?

About twenty-five years ago I invented an impossible rope trick by accident, and afterwards I could never figure out what I’d done or get the trick to work again. It wasn’t the rope that had vanished, but the trick itself. The incident took place at a math conference in Amherst, Massachusetts, and no, I hadn’t been drinking, though I admit that it was late at night and I was tired.

The trick consisted of forming two simple overhand knots on a rope, one right-handed and one left-handed, and passing one of them through the other in such a way as to cause the knots to cancel, leaving a simple unknotted rope.

Sounds natural, right? Except that math says that this can’t happen. And ironically it was in trying to show another conference participant that it can’t happen that I accidentally stumbled across a “demonstration” that it can.

Of course, when I say “math says”, what I mean is “mathematicians say” — mathematicians like John Conway, who (regardless of who wins this “world’s-most-interesting-mathematician” contest) is The World’s Most Interesting Mathematician; just read his biography, “Genius at Play” by Siobhan Roberts, if you don’t believe me. When Conway was still in high school, he found a beautiful way to prove that two knots on a rope can never cancel each other. I learned about Conway’s proof via Martin Gardner’s “Doughnuts: Linked and Knotted” (see the References).

Conway’s argument is a proof by contradiction; I’ll abridge Gardner’s explanation a bit. Suppose we have a rope with two overhand knots tied in it, called A and B, and we attach the two ends of the rope to opposite walls of a room. Imagine that the ends of the rope continue out two windows and join up again over the roof of the house, as in panel 1 of the picture below (taken from Gardner’s article).

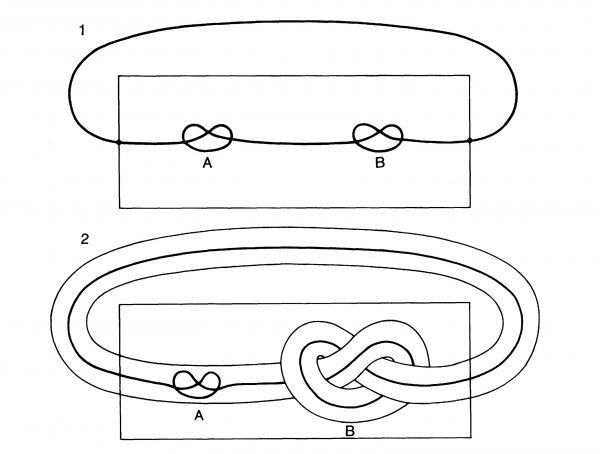
From p. 61 of “Knotted Doughnuts and Other Mathematical Entertainments” by Martin Gardner; permission pending

Imagine a sheath around the rope that swallows one knot (A) and follows the other (B), as in panel 2; the sheath, like the rope, goes out both windows, and the two ends of the sheath join over the roof. Notice that the sheath is knotted, with a single overhand knot.

Could there be a way to cancel A with B, converting the doubly-knotted rope into an unknotted rope (moving the sheath around as needed to get out of its way)? If so, consider what the end of the process would look like: we’d see an unknotted rope joining the two walls, with a sheath surrounding it. Would the sheath still have a knot in it? Yes, because it had a single overhand knot in it at the start, which no amount of twisting around can undo. But if the sheath is knotted at the end of the process, the rope it encloses must be knotted too! (For more details, see the Gardner article or the book-excerpt by Kauffman listed in the References.)

The upshot is, two overhand knots can’t cancel each other.

But that leaves us with the question, what exactly happened twenty-plus years ago when I got two overhand knots to cancel?

I still don’t know, and I suspect I never will, but by a wonderful coincidence, I recently learned that Professor Louis Kauffman invented and performs a trick of this type. (Kauffman, like Conway, has done a lot of work on knots — in fact, both of them have “knot polynomials” named after them, which sometimes enable you to replace the problem of telling when two knots are genuinely different by the much simpler problem of recognizing when two polynomials are unequal.) Here’s a video in which Kauffman demonstrates how you can, after all, get two overhand knots of opposite handedness to cancel one another:

So, what do we have here? A contradiction in mathematics? Maybe it’s something humbler but still astonishing: a proof that a single overhand knot in a closed loop actually can be removed from the knot without performing any cutting. After all, Conway’s proof hinges on the assertion that a sheath that’s knotted at the beginning of the process must still be knotted at the end.

Indeed, Kauffman has developed methods for creating and annihilating knots on a string without actually tying or untying them:

Obviously the technological implications of a way to remove knots from a closed loop without cutting it open would be world-changing. Kauffman claims that his demonstration makes use of Rupert Sheldrake’s morphogenetic field, but surely a more parsimonious explanation is that Kauffman pushes the rope into the fourth dimension when we’re not looking, right?

I’m pretty sure that Kauffman’s trick isn’t the maneuver I accidentally invented in Amherst, so I deserve zero credit for inventing his trick. Come to think of it, I don’t deserve credit for inventing “my” trick either. With very few exceptions (like Fermat), the mathematical community rightly honors the people who share their discoveries, not the people who claim to have made discoveries but don’t give the details, saying “I don’t have room” or “I forgot”.

A final possible solution to the mystery of the vanishing rope trick is supplied by variants of Murphy’s Law (“If something can go wrong, it will”). Remember how the impossible knot-cancellation occurred when I was trying to demonstrate Conway’s proof to someone? I propose a variant of Murphy’s Law that says “Even if something can’t go wrong, it still will — as long as a mathematician claims to be able to prove that it can’t.” Likewise, my failure to recreate the trick follows from yet another variant of Murphy’s Law: “If something can go wrong, it will — unless, of course, you want it to.”

Thanks to John Baez, Sandi Gubin, Lou Kauffman, Scott Kim and Andy Latto.

ENDNOTES

All morphogenetic/multi-dimensional kidding aside, the most likely explanation for what happened is that I misdirected my attention somehow. If I could learn to misdirect other people’s attention in the same way, I’d have a pretty cool trick!

REFERENCES

Martin Gardner, “Doughnuts: Linked and Knotted”. See Chapter 5 in Gardner’s book “Knotted Doughnuts and Other Mathematical Entertainments” or Chapter 20 in “The Colossal Book of Mathematics”.

Louis Kauffman, “Knot Logic”. A three-page excerpt that explains Conway’s argument is posted on the Mathematical Enchantments website, with Kauffman’s permission.

Louis Kauffman has made a number of YouTube videos of knot tricks. I already included links to Kauffman’s (K)not Cancellation and Collapse (marked “KnotAnomaly” above) and WhiteFigureEight1073. Kauffman and Allison Henrich are writing a book on Rope Magic and Topology. In the meantime, you might also enjoy Chefalo Rope Trick and Chefalo Rope Trick and Ring Drop. Also, if you ever find yourself in a time-loop (as in the movie Groundhog Day), and need a way to pass the same hours over and over again, don’t train yourself to throw cards into a hat the way Bill Murray’s character does; instead, train yourself to throw a knot in a rope! Bri Crabtree can do it; you can too.

Zoe Griffiths – The aeroplane seating problem

Zoe Griffiths is a maths communicator for Think Maths. You can find her on Twitter at @zoelgriffiths.

Zoe has prepared a video about a probability problem that takes place on an aeroplane.

So, which bit of maths has tickled your fancy the most? Vote now!

 Loading ...

The poll closes at 9am BST on the 9th. Whoever wins the most votes will get the chance to tell us about more fun maths in round 2.

Come back tomorrow for the last match in round 1, pitting Jo Morgan against Tony Mann, or check out the announcement post for your follow-along wall chart!