This is the penultimate round of the hottest contest of the summer, The Big Internet Math-Off. We’re down to 4 competitors, each raring at the bit to show us more fun maths. In this first semi-final, we’re pitting Nira Chamberlain against Zoe Griffiths.
The rules are the same as always: take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!
 Nira Chamberlain – Schelling’s model
Nira Chamberlain – Schelling’s model
Dr Nira Chamberlain is an applied mathematician and maths outreach expert, and Vice President, Professional Affairs and Industry at the IMA. You can find him on Twitter at @ch_nira, or at nirachamberlain.com. In round 1 he saw off James Tanton with an application of the Reynolds equation to Formula 1 cars, and then in round 2 gave us a history lesson on the black heroes of mathematics.
Nira has made a video about Schelling’s model.
 Zoe Griffiths – The ‘phantom’ parabola
Zoe Griffiths – The ‘phantom’ parabola
Zoe Griffiths is a maths communicator for Think Maths. You can find her on Twitter at @zoelgriffiths. She won her round 1 match with a probability puzzle on a plane, and then rocked the vote in round 2 with Benford’s law.
This is the closest you’ll ever get to a maths ghost story – meet the ‘phantom’ parabola that hangs, unnoticed, perpendicular to every quadratic and allows us to visualise complex solutions.
Roots of quadratics with real coefficients come in one of three situations; either the parabola intersects the $x$-axis twice giving us two real solutions, or it turns on the $x$-axis making one repeated real solution, or it never reaches the $x$-axis. In this final situation, we know that instead of real solutions we have a (conjugate) pair of complex solutions that cannot be represented on our real $x$-axis.
It seems incomplete to not have the corresponding visualisation of complex solutions. This, after all, is an area of mathematics that showcases the powerful and elegant unity that exists between the algebraic and graphical representations, as dreamt up by Descartes all those years ago. But then it breaks down when those solutions are complex. How dissatisfying!
Enter the ‘phantom’ parabola! The complex solutions of the quadratic sit on this ‘phantom’ which hangs ‘upside down’ and at right angles to the original, with the two parabolas meeting at their extremes.
And we can plot the ‘phantom’ parabola if we represent the values not on a one-dimensional $x$-axis, but on a two-dimensional ‘$x$-plane’, that has a real axis and an imaginary axis. The $y$-axis is then perpendicular to this plane. Read the steps of the argument below:
- We are finding the roots of the general quadratic $y=a(x-b)^2 + c$ where the constants are real. To
make the algebra neater, let $v=x-b$ so the quadratic is $y = av^2 + c$. - Since $v$ is complex let $v = m+ni$, where $m$ and $n$ are the axes of the complex ‘$x$-plane’.
- We will now look for the values of $v$ when $y=0$. From these we could easily work back to
find the values that $x$ takes when $y=0$. - $y$ is real and therefore $v$ must either have only a real component or only an imaginary
component (which when squared would become real). - If $v$ is real then $n=0$ and $y=am^2+c$. (This quadratic is the original one).
- If $v$ has only an imaginary component then $m=0$ and $y=a(ni)^2+c$ which simplifies to: $y=-an^2+c$. This is the ‘phantom’ parabola!
See a specific parabola and its ‘phantom’ in the plot below.
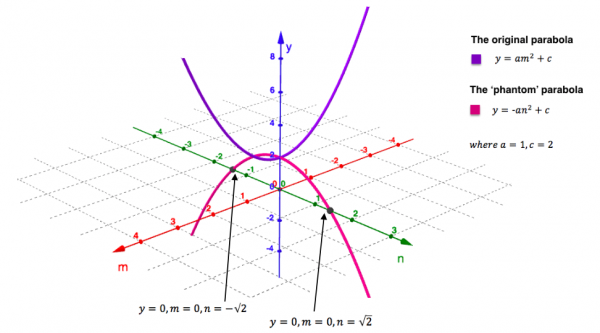
Finally we glimpse the complex solutions! The quadratic in this case ($y=v^2+2$) has roots at $v=\pm\sqrt{2}i$ which can be found at the points marked above where the ‘phantom’ curve crosses the plane with equation $y=0$ (the complex ‘$x$-plane’). This is of course analogous to where real solutions of a quadratic appear on a 2D plot.
Every parabola has a ‘phantom’ and if we plot both it and the original parabola we will always be able to visualise the two roots of the quadratic.
In the case when the two roots are real and distinct the ‘phantom’ turns before the complex ‘$x$-plane’, with the original curve crossing the plane instead.
And in the case when we have what we call a ‘repeated’ real root? Well, how befitting is it that in this situation we have two curves, the original and the ‘phantom’, both touching the ‘$x$-plane’ in the same place but from opposite directions.
Never again must we take it blindly on trust that every quadratic has two solutions!
Click here for an interactive plot of the general quadratic and its ‘phantom’. Vary the constants $a$ and $c$ and see for yourself the two solutions of the quadratic in each different situation!
I was first introduced to the ‘phantom’ parabola whilst on a course run by MEI. They in turn referenced the work of maths teacher Philip Lloyd. Philip developed this idea to help his students understand complex roots. He was the first to describe these curves as ‘phantom’.
But it is not only the quadratic that has a ‘phantom’! For even more excitement check out Philip’s website where he leads us through the derivations and properties of the ‘phantoms’ of other functions – from ‘phantom’ cubics to ‘phantom’ hyperbola! It is beyond pleasing.
Mathematics has once again made the invisible, visible.
With many thanks to Ben Sparks for making my ambitions of an interactive GeoGebra plot a reality!
So, which bit of maths has tickled your fancy the most? Vote now!
Semi-final 1 - Nira Chamberlain v Zoe Griffiths
- Nira Chamberlain with Schelling's model
- (50%, 513 Votes)
- Zoe Griffiths with a phantom parabola
- (50%, 504 Votes)
Total Voters: 1,017
This poll is closed.
The poll closes at 9am BST on the 20th. Whoever wins the most votes will get the chance to tell us about more fun maths in the final.
Come back tomorrow for the other semi-final, pitting Edmund Harriss against Matt Parker, or check out the announcement post for your follow-along wall chart!

Vote Nira Chamberlain
The phantom parabola is really neat! I just wanted to point out what looks like a small typo to me. For the phantom parabola, I think the square root on the 2 is covering the i as well, when it shouldn’t.
Thanks! Fixed.
Thanks Jeremy for spotting that! Glad you like it.
Kenneth Kendig wrote a whole book about these phantom parabolas, called “Conics”. It’s great!
I like Dr Chamberlains Schelling model as it can be used in social science to understand how we can improve communication and productivity by creating an environment where every one is involved and feel committed to a common cause.
It can also be used in healthcare where the big issues often revolves around inequality in care and provision of special services for minority groups…i.e. how would schellings model address a universal care model in the elderly population..where individuals may want preferences along ethnic line and how do we ensure that the quality of care is the same in all social groups if this is possible.
Have a look at https://ncase.me/polygons/ for an explorable explantation of Schelling’s model.
Good luck Mr Chamberlain
Voted for Nira Chamberlain
Good luck Dr Chamberlain!
What happens when the $b$ coefficient of the parabola isn’t zero?
What happens when there’s a multiplicity greater than 2 like y = (x -2)^3 ? How does the phantom parabola idea work there?