This is the third match in round 2 of The Big Internet Math-Off. Today we’re pitting Evelyn Lamb against Zoe Griffiths.

The rules are the same as in round 1: take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!

Evelyn Lamb – Sphere packing in 8 and 24 dimensions

Evelyn Lamb is a freelance math and science writer based in Salt Lake City, Utah, USA. She writes the blog Roots of Unity for the Scientific American blog network and co-hosts the podcast My Favorite Theorem with Kevin Knudson. You can find her on Twitter at @evelynjlamb, on Instagram at @evelynjlamb, or subscribe to her newsletter, Stuff Evelyn wants you to read. She got through round 1 with the very holey Wallis sieve.

Two years ago (Pi Day 2016, to be precise), Maryna Viazovska uploaded a preprint to the arxiv that solves the sphere-packing problem in dimension 8. The next week, she and some coauthors extended her work to the 24-dimensional case. (A sphere in any dimension is the set of points exactly one unit away from one central point. In dimension 2, that’s a unit circle. In dimension 3, it’s like the skin of a beach ball.) I wrote about the breakthrough for Scientific American.

There are a lot of things to enjoy about sphere packing in 8 and 24 dimensions. One is just how weird it is that we know the answers in dimensions 1, 2, 3, 8, and 24, which is a weird list of numbers. The one-dimensional case is just silly. In two dimensions, Henry Cohn, a researcher I talked about for an article about the breakthrough, describes each dimension as having its own idiosyncrasies. Part of the reason dimensions 8 and 24 were solved before 4, 5, 6, etc. is that there are these exceptionally nice lattices in those dimensions, $E_8$ and the Leech lattice, that were very good candidates for winning sphere packings. But in dimension 10, for example, the best known packing doesn’t even use a lattice, so it’s less regular than one might expect an optimal packing to be. When I talked to him, Cohn talked downright lovingly about $E_8$. It was very touching.

I am a fan of absurd things in general, so another thing I like about sphere packing is the absurdity of spheres in high dimensions. (Though I’m torn between this enjoyment and frustration at not having more visual intuition in those dimensions.) Spheres in dimensions 2 and 3 are round and seem full. They’re not much smaller than the circumscribing squares and cubes. But the volume of a sphere (actually a ball, but for some reason people talk about the sphere-packing problem, not the ball-packing problem, so I’ll keep using sphere throughout; in this context, the distinction is unimportant. Whether the spheres are empty or solid, they’ll pack the same. You aren’t allowed to deflate them to save space!) peaks in dimension 5, and after that they get smaller and smaller. By dimension 13, the volume is less than 1, and by dimension 100, it’s something like $10^{-40}$. There’s also a way in which we can think of high-dimension spheres as spiky, in the sense that a lot of their volume is not near the center of the figure the way it is in lower dimensions. That seems weird and silly and very un-sphere-like. It’s also related to the way the densest possible packings get less and less dense as dimension increases. (This relationship may not be monotone, but the overall trend is toward decreasing densities.) The spheres in higher dimensions are less convenient to pack because they are so decentralized.

Another cool aspect of this story is that high-dimensional sphere-packing is surprisingly useful. It’s obvious why we’d want to know the answer in 3 dimensions (that problem has a very interesting history as well, but I’m not going to go that much off-track), but it turns out higher-dimensional sphere packing is not just an academic exercise. They’re related to error-correcting codes and transmitting signals on noisy channels. I wrote about that in another post on Scientific American.

Finally, I think the sphere-packing problem is a great illustration of just how many simple mathematical questions there are that we still don’t know the answers to. For that matter, it was only a few years ago that the problem was solved and verified in three dimensions. And once you start digging into the history, you’ll find yourself learning about packing problems for other shapes and how we still don’t know the densest packings of pentagons, for example, or regular tetrahedra. There are so many fun questions to ask and a lot of opportunities for people to learn brand new things!

Zoe Griffiths – Benford Needs YOU!

Zoe Griffiths is a maths communicator for Think Maths. You can find her on Twitter at @zoelgriffiths. She won her round 1 match with a probability puzzle on a plane.

This quarter final pitch requires audience participation!

My video here explains all.

This pitch is all about Benford’s Law which fascinates me.

Benford’s Law tells us how frequently the digits 1 to 9 appear as leading digits in real-life data sets. We might expect each digit to have an equal chance of appearing as a leading digit – with each digit being a leading digit about one ninth of the time – but Benford’s Law tells us otherwise. Benford’s Law tells us that in fact the probability of the leading digit being a 1 is around 30%!

Here is a chart that shows the distribution predicted by Benford’s Law:

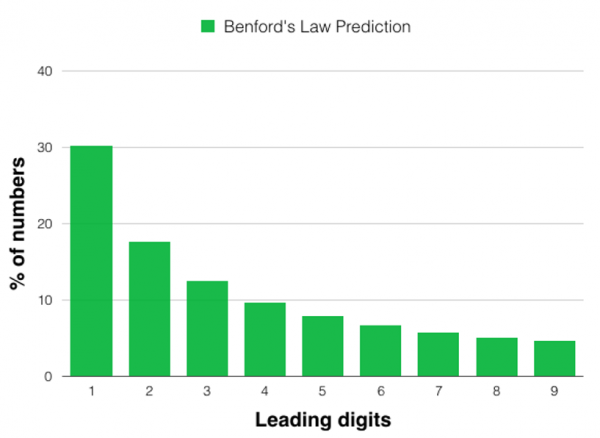
For a data set to follow Benford’s Law the data needs to span several orders of magnitude and be relatively unconstrained. Examples of data sets that follow Benford’s Law include the lengths of rivers and the population of countries.

Benford’s law is everywhere and has even been used to detect tax fraud! People fiddling the figures usually evenly distribute their fictional leading digits which Benford’s Law tells us is unlikely.

Now for the audience participation part: let’s make our own Benford’s distribution. To take part:

• Google the current population of the first place you think of that begins with the same letter as your first name.
• Go to my poll and vote for the leading digit of that population.
• Check out Benford’s distribution forming in real time in the chart below!

So, which bit of maths has tickled your fancy the most? Vote now!

 Loading ...

The poll closes at 9am BST on the 15th. Whoever wins the most votes will get the chance to tell us about more fun maths in the semi-final.

Come back tomorrow for our final match in round 2, pitting Matt Parker against Jo Morgan, or check out the announcement post for your follow-along wall chart!