
Here’s the second match in Round 1 of The Big Internet Math-Off. Today, we’re pitting Samuel Hansen against Paul Taylor.
Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!
Samuel Hansen – Your friends have more friends than you do
 Samuel Hansen is a prolific mathematical podcaster. His credits include Strongly Connected Components, Combinations and Permutations, the Math/Maths podcast, and his current project, Relatively Prime. You can find him on Twitter at @samuel_hansen or at samuelhansen.com.
Samuel Hansen is a prolific mathematical podcaster. His credits include Strongly Connected Components, Combinations and Permutations, the Math/Maths podcast, and his current project, Relatively Prime. You can find him on Twitter at @samuel_hansen or at samuelhansen.com.
Listen below to Samuel’s story of why you, well not you, but definitely why for everyone you know, their friends have more friends than they do and how this paradox can help fight epidemics.
Now that you have listened you will of course want to find out more about why your friends have more friends than you do. In order to do this you can read Scott’s paper, check out Nicholas’s work, or listen to the season one Relatively Prime episode featuring a longer version of this story. Samuel also wrote an expository piece about the friendship paradox for Second-Rate minds that you might want to check out. And Samuel wants to thank y’all for your votes!
Music and Effects credits:
Ken MacLeod
tim.kahn
dr_skitz
DickBlox
misjoc
Paul Taylor – How to really know Pythagoras’ theorem is true
 Paul Taylor is a data analyst, occasional crossword setter, and occasional Aperiodical contributor. He has a thing about analysing the rules of TV game shows. You can find him on Twitter at @apaultaylor.
Paul Taylor is a data analyst, occasional crossword setter, and occasional Aperiodical contributor. He has a thing about analysing the rules of TV game shows. You can find him on Twitter at @apaultaylor.
How To Really Know Pythagroas’ Theorem Is True
My aim in this pitch is to convince you that the most famous fact about right angled triangles, Pythagoras’ Theorem, is not only true, but is really obviously true. Here’s an example fact about right-angled triangles to demonstrate my bar for ‘really obvious’.
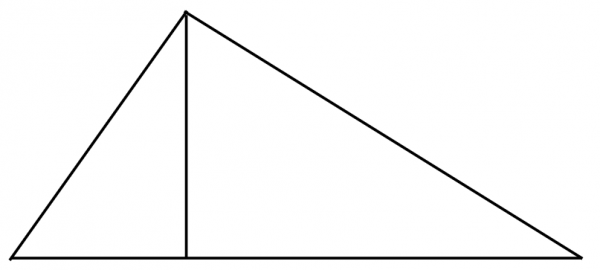
Fact: the two smaller triangles are congruent to the big one.
Both of the small triangles have a right angle, and both share one angle with the big triangle. If triangles have two angles in common, the third must be too, since they all add up to 180°. Obvious, see.
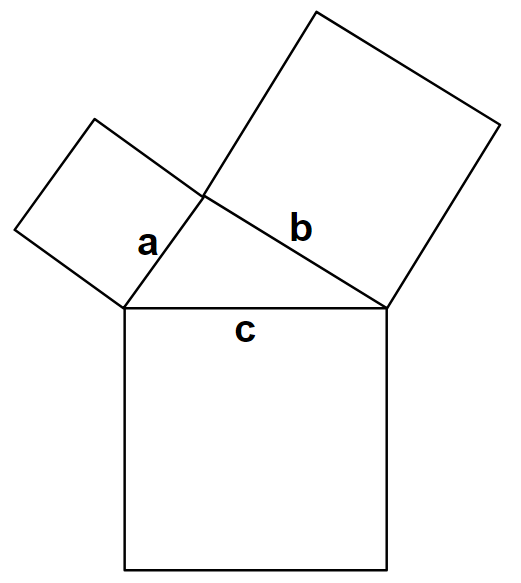
Pythagoras’ Theorem doesn’t seem so obvious. Famously, it claims that when you draw squares on all three sides of a right-angled triangle, the large square has the same area as the two smaller squares combined. Since the area of a triangle is the square of its side length, this gives the equation form of the theorem, a²+b²=c².
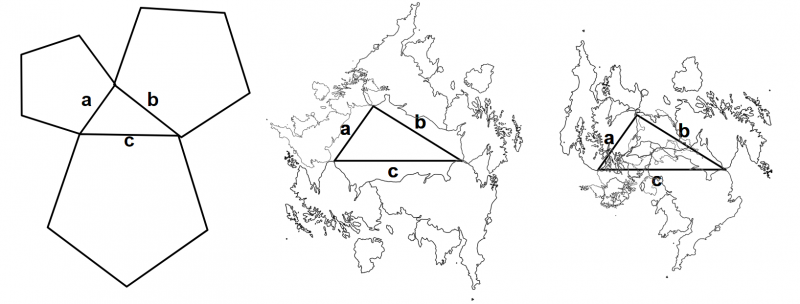
But there’s no reason to use squares, really. For any shape, if you pick any line segment on it to stand in for the side of the square, the shape’s area is proportional to the length of the side squared. So if we can make an equivalent version of Pythagoras’ Theorem with any shape replacing the squares that’s obviously true, so will be the square-y version. There’ll be an ugly common factor throughout the equation but it will be equivalent. Here are a couple of examples with different shapes: pentagons (using one of their sides as the nominated line) and maps-of-Britain (using a line roughly from Peterhead in Scotland to Great Yarmouth). And another obvious point: it doesn’t matter which way round we draw the shapes, so I’ve added one with the maps-of-Britain facing inwards. They overlap in a pretty ugly way, but again, if we could prove the areas of the two little Great Britains add up to the area of the great Great Britain we’d have proved the theorem.
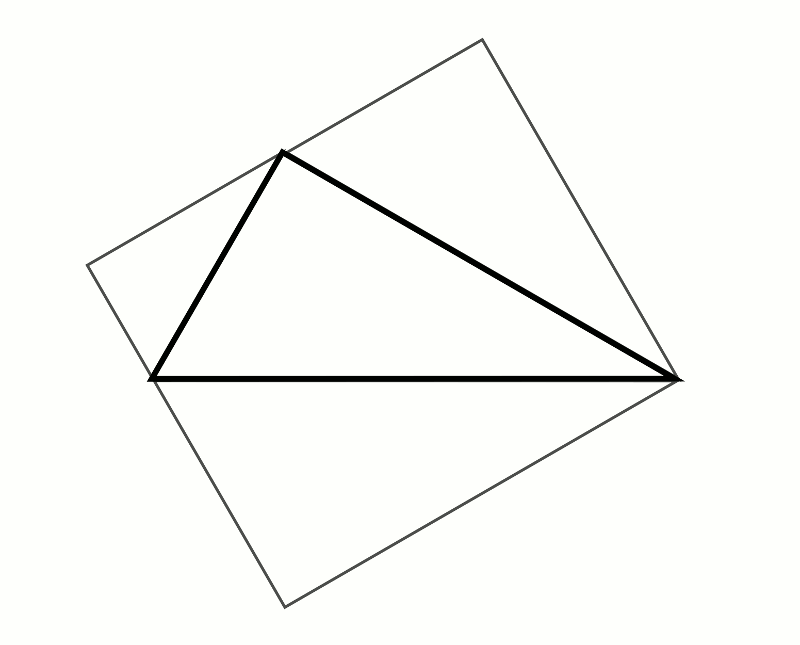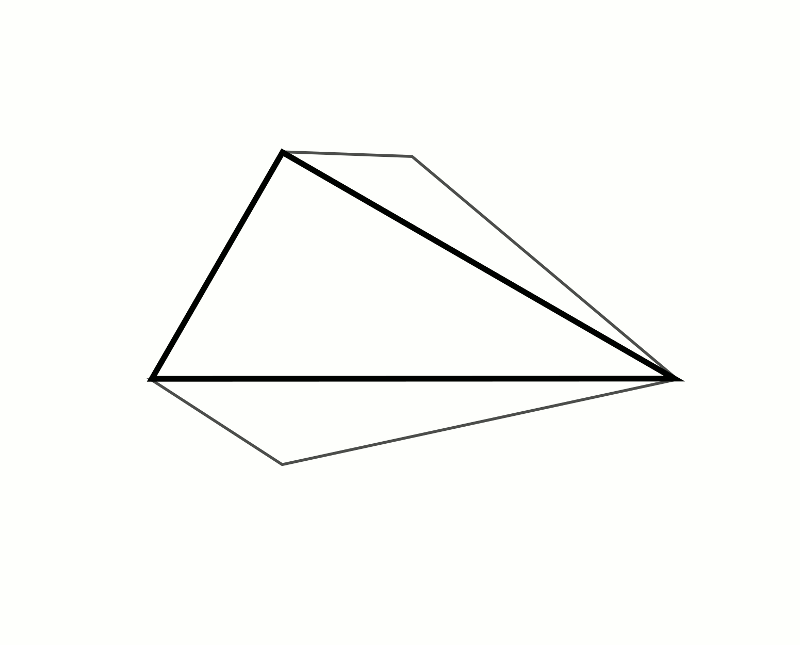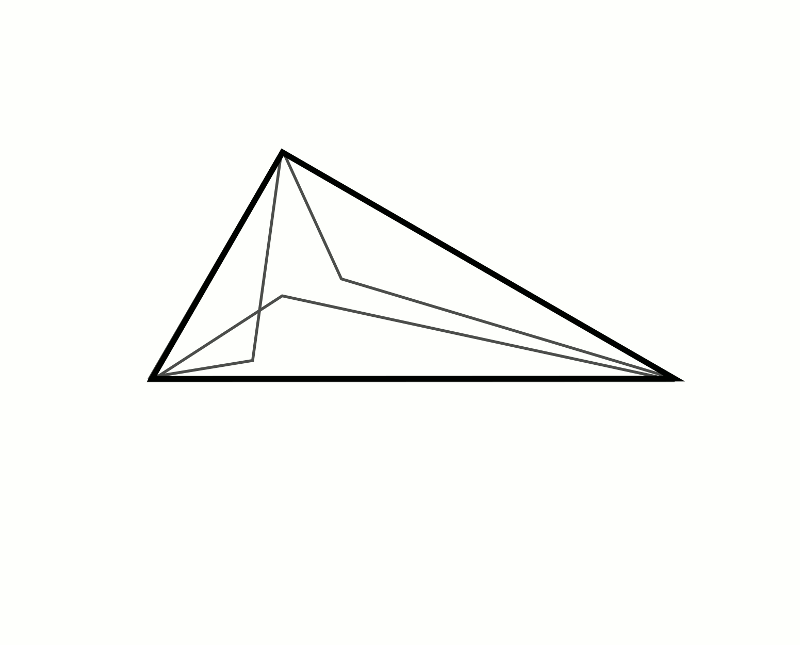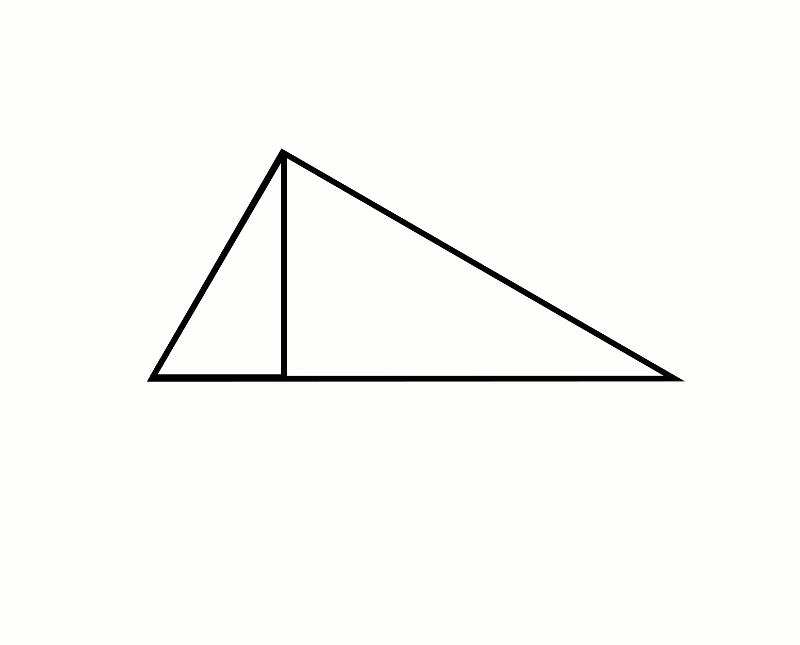
This doesn’t seem very elegant though; these are pretty weird arbitrary shapes to introduce. But there’s one encouragingly ‘meta’ candidate to use: the right-angled triangle itself. Let’s use its hypotenuse as our nominated line segment, and just for kicks, we’ll have the triangles initially facing out, then with a whizzy GIF show what they look like facing inwards.
Oh look! It makes that picture from the start. Remember we decided it’s obvious the smaller triangles in this picture are congruent to the big one. And their hypotenuses are on the smaller sides of the triangle, so this is the correct set-up. (The triangle we’ve drawn on the hypotenuse of the main triangle completely overlaps the main triangle of course.) So now it’s obvious the two smaller shapes’ areas add up to the larger shape’s area – they’re actually there, occupying the same physical area on the screen. Pythagoras’ Theorem is thus not just proved, but rendered completely obvious.
So, which bit of maths has tickled your fancy the most? Vote now!
Round 1 match 2 - Hansen v Taylor
- Paul Taylor with an obvious proof of Pythagoras' theorem
- (53%, 112 Votes)
- Samuel Hansen with more friends than you
- (47%, 99 Votes)
Total Voters: 211
This poll is closed.
The poll closes at 9am BST on the 4th. Whoever wins the most votes will get the chance to tell us about more fun maths in round 2.
Come back tomorrow for our third match in round 1, pitting Peter Rowlett against Alison Kiddle, or check out the announcement post for your follow-along wall chart!
2 Responses to “The Big Internet Math-Off, Round 1 – Samuel Hansen v Paul Taylor”