Here’s the second match in round 2 of The Big Internet Math-Off. Today we’re pitting Paul Taylor against Edmund Harriss.

The rules are the same as in round 1: take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!

Paul Taylor – Non-transitive dice and Non-non-transitive dice

Paul Taylor is a data analyst, occasional crossword setter, and occasional Aperiodical contributor. He has a thing about analysing the rules of TV game shows. You can find him on Twitter at @apaultaylor. He secured victory in round 1 with an unconventional proof of Pythagoras’ theorem.

You might have heard of a mathematical diversion called non-transitive dice. If you and a friend play the game of ‘pick one die each and roll them, and whoever gets the higher number wins’ with a set of non-transitive dice, an interesting thing happens. Because each die in the set has a different arrangement of numbers on it, some are more likely to win against others. In the simplest set there are three dice: let’s say they’re coloured red, green and blue. Roll red against blue, and red is more likely to win. Roll blue against green, and blue is the favourite. So red beats blue and blue beats green. But roll green against red, and green is likely to win. Red beats blue beats green beats red beats…. This ‘no-best-die’ effect is what makes the dice non-transitive.

The basic set of non-transitive dice: the faces you can’t see are numbered the same as the ones opposite, so each number occurs twice on each die

The property of numbers being bigger than other numbers is nice and transitive: 9 is bigger than 6 and 6 is bigger than 4, so 9 is bigger than 4. But by transferring the situation to a probabilistic dice-rolling world, we’ve broken the transitivity.

So one day I wondered: if we can break transitivity by putting it onto dice, can we break non-transitivity the same way? That is, can we take a set of symbols with a relation between them that isn’t transitive, and arrange them on a set of dice so that there is a best dice to choose in the pick-one-each-and-roll game?

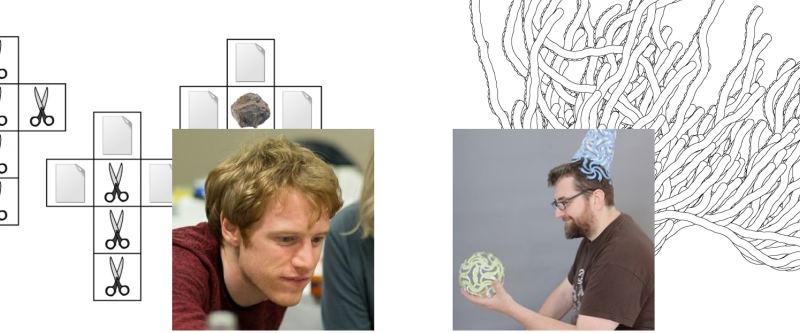
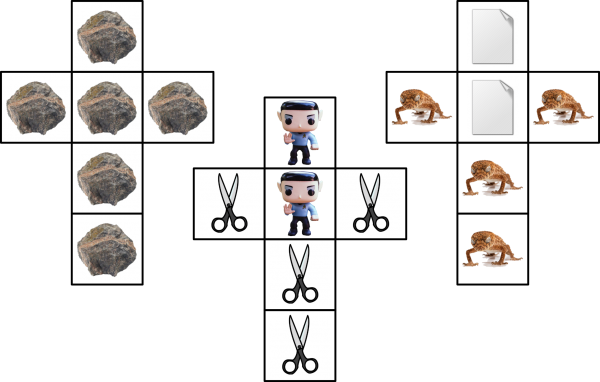
Well, the answer is: yes we can! Here, in net form for ease of analysis, I present the world’s first non-non-transitive dice.

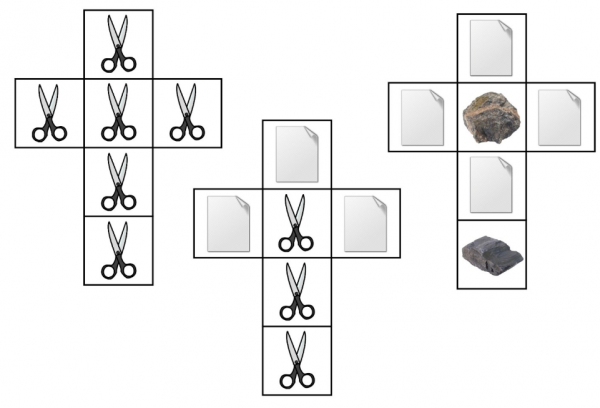
Note: I have no grounds for the claim that these are actually the world’s first. In any case they are already six years old, as I first presented them at the MathsJam 2012 gathering.

Although rock, paper and scissors each have exactly equivalent power in the children’s game, here the all-scissors die is best, beating the scissors-and-paper die 50% of the time and never losing to it, and beating the paper-and-rock dice two-thirds of the time. The rock-and-paper die is the weakest, being more likely to lose against either of its opponents.

Unfortunately, with only three symbols to split across the dice, rock-paper-scissors non-non-transitive dice involves a lot of draws. Luckily, helpful nerds have come up with a five-symbol version of the game, Rock Paper Scissors Lizard Spock. In addition to the normal rules, Lizard poisons Spock and eats Paper, but is crushed by Rock and decapitated by Scissors; Spock smashes Scissors and vaporises Rock, but is ‘disproved’ by Paper. This forms a non-transitive set of five items, each beating and losing to two others. Using these, I’ve come up with a set of never drawing, non-non-transitive dice.

Here the all-rock die beats either of the others two-thirds of the time, and the scissors-Spock die beats the lizard-paper die by the same margin.

Now, non-non-transitive dice are not perhaps that mathematically illuminating. Non-transitive relations can have transitive subsets, so ‘breaking’ one like this is really pretty easy. (I could have made a set with an all-rock, an all-scissors and an all-lizard die, which you could say would technically meet my definition, with 100% win margins to boot, but it would probably be considered cheating). But I think they’re fun anyway, and perhaps they’ll remind people always to keep an eye out for novel ways to extend interesting bits of maths.

Edmund Harriss – The Collatz sequence

Edmund Harriss is a mathematical artist and a professor at University of Arkansas. Among other things, he’s the co-author of Snowflake, Seashell, Star, a mathematical colouring-in book. You can find him on Twitter at @Gelada, or on his homepage. He got through round 1 with a blatant appeal to the Aperiodical’s readership, in the form of a set of aperiodic Penrose tiles.

The mathematics we know is not a complete field of knowledge, despite how it can feel in school. It is small islands in a vast sea. As a simple example, even our best mathematicians do not understand the relationship between multiplying by 3 and dividing by 2! Let me explain.

Take a number, if it is even divide by two, if it is odd, add one, then divide by 2, what will happen as you repeat this? 9 will go to 5, then to 3, then to 2 and 1, 1 stays at 1. Any number you start with, other than 1 will go to something smaller. When we get to 1 we stay there. All whole numbers will end up at one.

This gives a simple example with division by 2. To combine this with multiplication, we apply the rule $(3x+1)/2$, in other words, multiply by 3, add 1 and then divide the result by 2. Now 9 goes to 14, 7, 11, 17 and then 26 this is jumping all over the place and is much larger than 9. 26 does drop to 13, then back up to 20, 10, 5, 8, 4, 2 and finally 1. Now 1 jumps back to 2 and a loop begins. It took a while but 9 made it to this loop. Our previous argument does not work though as although dividing by 2 does still make things smaller, multiplying by 3 then dividing by 2 makes the number larger as we saw for 9. Choose a number and try it for yourself!

Note that we have already shown that 1, 2, 4, 5, 7, 8, 11 and 13 all get to the loop, as they all fell on the path that 9 takes, so many small numbers do work. If you really love to do arithmetic or want to keep someone else quiet for a time try with 27!

All numbers that have been tested do come back to this loop of 1, 2, but there is no proof that this will always happen, to have a sense of how the pattern is complicated I created the picture above. This shows the paths that numbers to 60,000 take, to come back to the 1,2 loop (in order to include everything up to 60,000 it has many larger numbers as well). The path turns left if the number halved and right if it tripled and added 1. All the paths are lined up to meet at the same place. Here is an early segment.

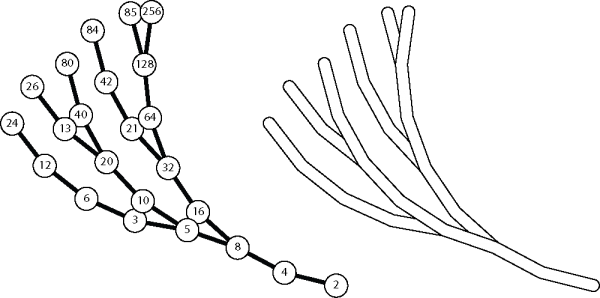
As this image grows, it looks more like seaweed or a Lovecraftian horror than rigid mathematics. Perhaps that form shows why the patterns are not easy to find?

You might ponder why can you always divide by two in the odd number case? Or you could explore what happens for other numbers, perhaps multiply by 5 instead or add 3, maybe think about how you would need to change this to divide by 3, instead of 2. Whatever you do though, do not try to prove this, it is a trap that has ensnared many great minds with its seeming simplicity! In fact the great mathematician Paul Erdös said that “Mathematics is not yet ripe enough for such questions.”

This image was created for my colouring book Visions of Numberland (Visions of the Universe in the US).
It was also discussed on Numberphile. For more on the Collatz conjecture, the Wikipedia page is quite good, but if you really want the academic state of the art I recommend Jeffrey Lagarias’ wonderful book. You might also look at Conway’s proof that a general version is undecidable, meaning that we cannot prove whether that version is true or not!

So, which bit of maths has tickled your fancy the most? Vote now!

 Loading ...

The poll closes at 9am BST on the 14th. Whoever wins the most votes will get the chance to tell us about more fun maths in the semi-final.

Come back tomorrow for our third match in round 2, pitting Evelyn Lamb against Zoe Griffiths, or check out the announcement post for your follow-along wall chart!