Here’s the second match in round 2 of The Big Internet Math-Off. Today we’re pitting Matt Parker against Jo Morgan.
The rules are the same as in round 1: take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!
Matt Parker – The projective plane
Matt Parker is a standup mathematician with a lot of jobs. He’s one third of the scientific comedy group Festival of the Spoken Nerd, author of the book Things to Make and Do in the 4th Dimension, he sells mathematical toys at Maths Gear, he frequently features on Numberphile, and he does stuff for schools through Think Maths. You can find him on Twitter at @standupmaths, on YouTube, or at standupmaths.com. He got through round 1 with a pile of matchboxes that can play noughts-and-crosses.
Of all the surfaces in maths, the real projective plane is one of the more enigmatic. It can be thought of as the collection of all lines which go through the origin in 3D, but I like to view the real projective plane as the result of sticking a Möbius loop to a disc.
You can cut a disc out of paper: it’s a nice 2D surface with one edge going all the way around it. You can make a möbius loop out of paper, which is also a surface with a single edge going all the way around. If that one edge of a möbius loop were to be stretched into a circle it could be neatly attached to the one edge of a disc… making a kind of twisted sphere. At this point, paper is no longer fit for purpose. To avoid awkward self-intersections this only works properly with four spatial dimensions.

I first met the real projective plane this way over a decade ago when a maths teaching friend of mine showed me a low-resolution capture of what must have been a VHS tape. It was an animation made in 1992 by the University of Wales and IBM. A relic from a previous age of maths communication. It started with a line sweeping around to represent all possible lines going through the origin.


Through a series of steps the video goes through things which are equivalent to this set of all possible lines. For a start, we don’t need to extend each line infinitely far; cutting them off within a unit sphere does not reduce the number of lines. In fact, each line does not need to be drawn, we only need the two points where it touches the sphere.

Actually, a whole sphere is rather wasteful. As each line has no direction a single hemisphere is all that is required, with every line represented by a single point on its surface. Except the hypothetical line sweeping around means that as the point goes off one edge of the hemisphere it appears on the opposite side. This is a disc but with some matching rules for how the top should be sealed up. Once it is closed according to how the dot moves we will be left with the real projective plane.
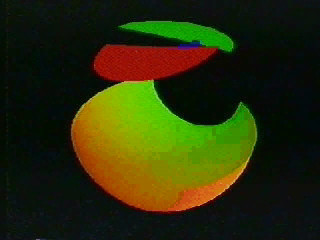
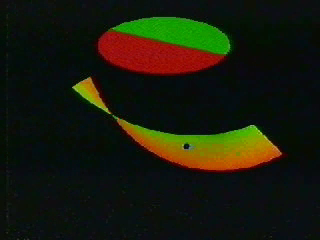
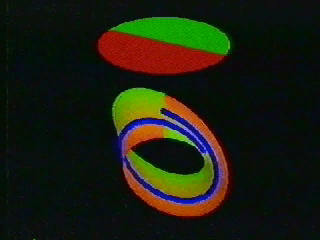
I will leave you to watch the rest of the video if you wish. I dug through an old archive hard-drive of mine to find the long forgotten file. It’s four minutes of slow, soundless topology. But without a word or symbol it shows how the dot moving on a hemisphere can then be split into a disc and a möbius loop.
Maybe one day I’ll try to track down the original. Or make a new new 4K version so more people can enjoy the real projective plane. I admit that it is not amazing as the Klein Bottle but the real projective plane is at least worth a second thought.
Acknowledgements:
Thanks to Sarah Aldous who showed me this video many years ago and continues to work as an amazing mathematics teacher. There is more about the real projective plane and the project which produced this video on this website from 1997.
 Jo Morgan – the Klein bottle
Jo Morgan – the Klein bottle
Jo Morgan is a maths teacher, and owner of the resource site resourceaholic.com. You can find her on Twitter at @mathsjem. She won her round 1 match with that fascinatingly fiddly paper toy, the hexaflexagon.
The realm of topology is full mathematical wonders that we can ponder and adore even if we don’t fully understand what on earth’s going on. Klein bottles are complicated yet delightful, and they come with a quirky twist that has really captured my heart.
In 1882, German mathematician Felix Klein imagined sewing two Möbius strips together to create a single sided bottle with no boundary. Its inside is its outside! This lovely limerick by Leo Moser describes the simple idea behind what is a very complex topological construct:
“A mathematician named Klein
Thought the Möbius band was divine.
Said he: “If you glue
The edges of two,
You’ll get a weird bottle like mine.”
Unfortunately Klein bottles can’t actually exist in our universe. Damn those pesky dimensions! A true Klein Bottle requires four dimensions because the surface has to pass through itself without a hole. But that doesn’t stop the wonderful company Acme from selling their own zero-volume bottles which are basically like three dimensional photographs of ‘true’ Klein Bottles.
And this is where is gets cool. Because Cliff Stoll, the man behind Acme Klein Bottle, is absolutely brilliant. Browse his website and you’ll see what I mean. You can buy anything from a Wine Bottle Klein Bottle (filling it with wine is not recommended!) to a Topless Teapot.
I am lucky enough to own one of Acme’s wonderful Klein Bottles (‘imported from the 4th dimension’) – it’s worth buying one even if just for the hilarious notes that accompany it.
“We note that your purchase order did not specify the number of spatial dimensions in the receiving universe. Rather than send a separate inquiry, we have taken the liberty of shipping three-dimensional products”.
“For best results, avoid doing stupid things”
I once took my Klein Bottle into school to show it off to my mini-mathematicians – they looked at it wide-eyed like it was from another planet. They convinced me to put water in it – in hindsight, this was not a sensible classroom activity!
There are a number of fantastic Numberphile videos about the wonderful world of Klein Bottles. This is a great place to start:
However to fully appreciate just how quirky and wonderful this gets, “The man with 1,000 Klein Bottles under his house” is a must watch. It features a homemade forklift robot! Once you’ve watched it, I won’t be surprised if you immediately add Acme Klein Bottle to your Christmas list.
So, which bit of maths has tickled your fancy the most? Vote now!
Round 2 match 4 - Matt Parker v Jo Morgan
- Matt Parker with the projective plane
- (58%, 248 Votes)
- Jo Morgan with the Klein bottle
- (42%, 177 Votes)
Total Voters: 425
This poll is closed.
The poll closes at 9am BST on the 16th. Whoever wins the most votes will get the chance to tell us about more fun maths in the semi-final.
Come back on the 17th for the first semi-final, or check out the announcement post for your follow-along wall chart!

While I really liked Matt’s projective plane visualisation, being introduced to the Acme website couldn’t be beaten.