This is the twenty-third match in our group stage: from Group 3, it’s Vicky Neale up against Sophie Carr. The pitches are below, and at the end of this post there’s a poll where you can vote for your favourite bit of maths.

Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!

Vicky Neale – Prime scarves

Vicky Neale is the Whitehead Lecturer at the Mathematical Institute and Balliol College, University of Oxford, which means her job is to be enthusiastic about mathematics with undergraduates, school students, and anyone else she can find.  She is the author of Closing the Gap: the quest to understand prime numbers. She’s @VickyMaths1729 on Twitter.

I am pleased to be able to reveal this winter’s mathematical must-have fashion accessory: the prime distribution scarf. It is available in a range of styles. Here you see the mod 6 and mod 7 versions accessorised with baby hedgehogs. Either would be the perfect Christmas gift for the mathematicians in your life.

If you prefer an extra-long scarf, don’t worry: happily there are infinitely many primes, so the scarf can be as long as you like and will still feature prime numbers right to the end. Although, as Grant described the other day, the primes will on average be more sparsely distributed as you move to very long scarves. The construction process means that it is inevitable that sometimes there will be large gaps between primes whereas sometimes they will be very close together, the manufacturer accepts no responsibility for this natural variability.

Each scarf is reversible, so there is no need to worry about putting it on the wrong way round.

Close inspection will reveal differences between the mod 6 and mod 7 versions. The mathematician wanting pattern and structure in their life might prefer mod 6, the mathematician preferring less rigidity and predictability might prefer mod 7. To avoid injuring yourself, you are encouraged to explore the distribution of the primes when the scarf is not round your neck.

There is a secret design feature with these scarves. You can roll your scarf into a cylinder, and the prime number design will join up perfectly, spiralling along the length of the scarf.

Discerning mathematicians will also be interested in these prime number bracelets.

Number theory notes

Enthusiasts will enjoy Andrew Granville’s three papers on proofs that there are infinitely many prime numbers.

I wrote about my prime number bracelets for Chalkdust.

The scarves and bracelets relate to Dirichlet’s theorem about primes in arithmetic progressions, and (ambitiously) to the Elliott-Halberstam Conjecture. This conjecture has not yet been proved, but proving it would help with making progress towards the Twin Primes Conjecture.

Knitting knotes

I used a technique called double knitting. This creates the reversible scarf: both sides are knitted simultaneously, there is no sewing up at the end. I have never used this technique before, and am very proud of myself for doing it — although it turns out not to be difficult! As the eagle-eyed knitters will notice, I have not yet tackled casting on or casting off using two colours. Here’s a picture showing the mod 6 scarf during the knitting process, to prove how I did it.

Design details

This was my third attempt at a design for the mod 6 scarf, but I’m glad I redid it (twice!), this one is better than my previous attempts. Mathematicians make mistakes. Mine this time was to forget to stop and think before doing mod 7. The blocks are 6 stitches high in the mod 6 scarf to make it possible to join the whole scarf into a cylinder with the design winding round neatly, so making the blocks 6 stitches high on the mod 7 scarf was not a smart move. I’ll undo it and rework it with blocks 7 stitches high, but not in time for this pitch! I’ll post pictures on Twitter when I’m done.

Sophie Carr – Bayes’ theorem

Sophie Carr is the founder of Bays Consulting. Having grown up building Lego spaceships she studied aeronautical engineering before discovering Bayesian Belief Networks which has led to a career she loves – essentially make a living out of finding patterns. She prefers fresh coffee over tea, pears over apples and her favourite flower is the tulip. She’s @SophieBays on Twitter.

My pitches in the group stages talk about the areas of maths that never fail to make me smile and so far I’ve talked about Bernoulli’s principle and the Navier Stokes equations. With this background information (supplemented by the fact I’ve previously stated I’d grown up loving aeroplanes) what probability would you have placed on my career has been in aeronautical engineering? How would you later that probability if I then told you that my first job was working in a flight evaluation team? Would the knowledge that it was my dream job make you further alter the probability my career involved working with aeroplanes? I adored my work and became interested in how to bring together and make the best use of all the information that was available. That interest completely changed my career due to a theorem developed by an English clergyman, published posthumously in 1762. I am still (and always will be) fascinated by aeroplanes, but the career changer was Bayes Theorem.

It’s possible you’ve never heard of Bayes Theorem which in the last few decades has gone from being a relative niche area of mathematics to one which affects many aspects of your daily life. In my view, Bayes Theorem is petite, stunningly elegant and quietly powerful.

But what does the Bayes Theorem do that is so amazing? Simply put it does something that we all intuitively do hundreds of times a day – it lets us update a probability each time we get new information or evidence. I’ll admit that at first glance this doesn’t sound so “oh-my-goodness-how-utterly-amazing-is-that-and-how-have-I-managed-without-this-all-my-life” However, that is the amazing part. Using probability theory, the Reverend Bayes produced a Theorem that lets us use all the information available to us: our belief; our judgement; our biases; our subjective opinion; what we’ve learnt from previous experiments or the overall weight of scientific knowledge and incorporate this in how to update a probability. This fact is incredibly powerful – it allows us to be open and upfront about the uncertainty in our data. It also allows us to incorporate how we intuitively reason into probability calculations. It also creates an enormous about of debate about the validity of the approach across statisticians and mathematicians alike. There are opponents to the use of Bayes Theorem but to me, it has always been the most natural way to work with probabilities.

If you’ve not seen or used Bayes Theorem before, a brilliant introduction into how you can update your views as information becomes available is through the use of the Monty Hall problem. This comes from a 1970’s game show called “Let’s Make A Deal”.

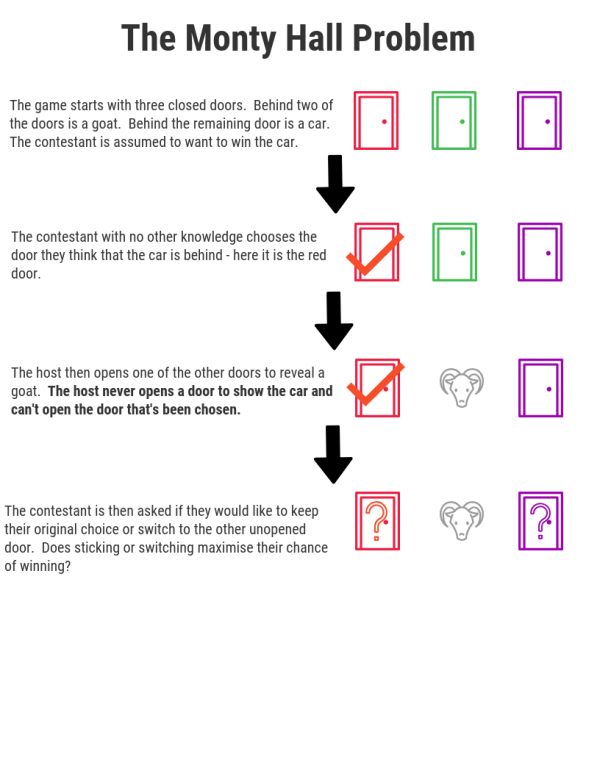
What would you do? Would you stay with the door you chose because you think there’s a 50/50 chance the car is behind either of the remaining closed doors? Would you switch your choice of doors just because you can? How can we work out the actual value of the information we’ve been given from the host opening up the door? The problem boils down to is this: What’s the probability that there is a car is behind the door that was originally chosen, given the door which was opened? How can you calculate that? This is where Bayes Theorem can help.

Putting maths in context always helps me, but as I don’t have three spare doors, goats or a car I’m going to answer the problem using cakes and sweets which I have to hand because I’ve been baking and eating quite a lot whilst writing these pitches. I’ve made three cakes and have hollowed them all out. Only one cake, however, has been stuffed full of sweets, that is the cake I am going to assume my helpful assistant will want to pick.

Let the game commence! My assistant has picked the red cake hoping the sweets are hidden there. She wants to know the probability that the sweets are hidden in the cake she has chosen given the cake I cut open – from this she can decide if she should stick with the pretty red cake or switch to the other, as yet unopened, cake.

Where to start? As the host:

• I can’t cut the red cake as this is the one selected by my assistant.
• Neither can I cut open the cake hiding the sweets.

So we can talk about a general result, I’m going to talk about cutting open the purple cake, mainly because that’s my favourite colour, but the result below would work if I talked about cutting open the green cake! Now we can get to the fun part of the game – Bayes Theorem for which we need to calculate:

1. The background (prior) probability that the sweets are hidden in each cake
2. The conditional probability that I’ll cut the purple cake given where the sweets are hidden
3. The unconditional (marginal) probability I’ll cut open one the purple cake

In Bayes Theorem the marginal probability is the denominator whilst the conditional and prior probabilities are multiplied together in the numerator. It really is that simple.

What’s the probability the sweets are hidden in each of the three cakes? With no other information about the cakes, my assistant can assume that there is an equal chance that the sweets are hidden in any one of the cakes. That means each cake has a one-third chance of hiding the sweets so we can write:

\begin{align}
P(\text{sweets are in the red cake}) &= \frac{1}{3} \\
P(\text{sweets are in the green cake}) &= \frac{1}{3} \\
P(\text{sweets are in the purple cake}) &= \frac{1}{3}
\end{align}

What’s the probability I’ll cut open the purple cake given where the sweets are hidden? Looking at all the options available in the game then we need to work out the probability I’ll cut the purple cake for each possible location of the sweets:

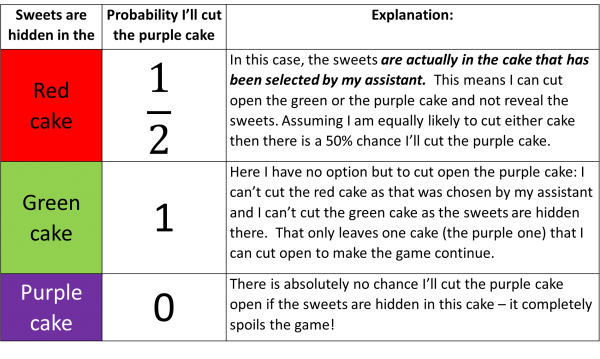
In maths notation we can write these results as:

\begin{align}
P(\text{I cut the purple cake} | \text{the sweets are in the red cake}) &= \frac{1}{2} \\
P(\text{I cut the purple cake} | \text{the sweets are in the green cake}) &= 1 \\
P(\text{I cut the purple cake} | \text{the sweets are in the purple cake}) &= 0
\end{align}

The unconditional (marginal) probability I’ll cut open the purple cake This is the sum of all the times I could cut open the purple cake and the easiest way to visualise this is with a probability tree:

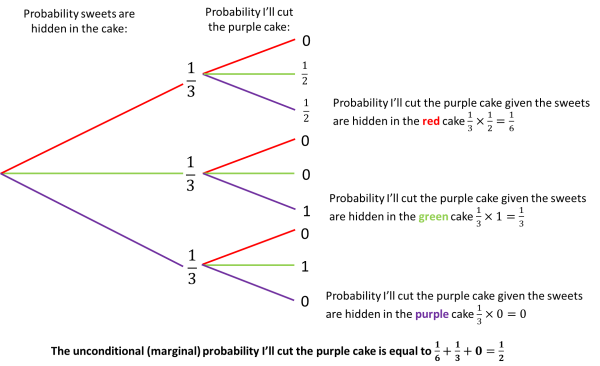
What my assistant really wants to know is the probability the sweets are in a cake given that I’ve cut open the purple cake? Let’s cut the cake and then put the numbers into Bayes Theorem:

\[ P(\text{sweets in the red cake} | \text{I cut the purple cake}) = \frac{P(\text{I cut the purple cake} | \text{sweets are in the red cake}) \times P(\text{sweets in red cake})}{P(\text{I cut the purple cake})} \]

\[ P(\text{sweets in the red cake} | \text{I cut the purple cake}) = \frac{\frac{1}{2} \times \frac{1}{3}}{\frac{1}{2}} = \frac{1}{3} \]

\[ P(\text{sweets in the green cake} | \text{I cut the purple cake}) = \frac{P(\text{I cut the purple cake} | \text{sweets are in the green cake}) \times P(\text{sweets in green cake})}{P(\text{I cut the purple cake})} \]

\[ P(\text{sweets in the green cake} | \text{I cut the purple cake}) = \frac{1 \times \frac{1}{3}}{\frac{1}{2}} = \frac{2}{3} \]

\[ P(\text{sweets in the purple cake} | \text{I cut the purple cake}) = \frac{P(\text{I cut the purple cake} | \text{sweets are in the purple cake}) \times P(\text{sweets in purple cake})}{P(\text{I cut the purple cake})} \]

\[ P(\text{sweets in the purple cake} | \text{I cut the purple cake}) = \frac{0 \times \frac{1}{3}}{\frac{1}{2}} = 0 \]

If my assistant decided to stick with the red cake, she has a one-third chance of getting the sweets. However, if she switches to the green cake she has a two-thirds probability of getting the sweets. So given this information, what would my assistant like to do?

But more importantly, did she get the sweets? Yes, she did. Happy tummy based on the assistant changing her mind. This example shows just how hard it is to intuitively combine information and update the final value as information is made available to you. It is so easy to overlook just how much information is included in the opening of a single door and how that information can help you understand if you should change your decision as to the probability of “winning” updates.

Admittedly this example will only help you get sweets (always nice) but it’s impossible to understate the overall impact of Bayes Theorem in your everyday life: medicine, finance, booking holidays, internet searching…the list goes on. Pretty much anywhere that you need to predict what will happen and update a probability as information becomes available. The tricky part is calculating or obtaining the probabilities needed for Bayes Theorem, especially if they are based on subjective evidence. In this situation the values used can be subject to huge debates – maths is not a subject where everything is known. It is a vibrant, dynamic topic to work in and Bayes Theorem is one area that lots of people are working on.

I started the group round by saying that I was going to make my three pitches on the areas of maths that always made me smile. That is true, but they are, with hindsight, also the areas of maths that made me go “ooooh, that’s counter-intuitive, how can that work?” I hope you’ve enjoyed reading about my favourite three topics and have had an “oooh, that’s cool” moment. Enjoy the rest of the competition!

So, which bit of maths do you want to win? Vote now!

 Loading ...

The poll closes at 9am BST on the 24th. Whoever wins the most votes will win the match, and once the group stages are over, the number of wins will determine who goes through to the semi-final.

Come back tomorrow for our last match of the group stages, featuring Colin Beveridge and Becky Warren. Or check out the announcement post for your follow-along wall chart!