This is the sixteenth match in our group stage: from Group 4, it’s Kyle D Evans up against Anna Haensch. The pitches are below, and at the end of this post there’s a poll where you can vote for your favourite bit of maths.
Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!
Kyle D Evans – Fred the lazy frog

Kyle D Evans is an award-winning maths communicator, musical comedian, teacher and general jack of all mathematical trades. He’s @kyledevans on Twitter.
Fred is a lazy frog. His first jump of every day is a proud half metre, but after this tiredness kicks in and every leap is half the length of the previous. Here are two proposals:
a) Fred is always moving forwards, so if he jumps enough times he can cover any distance he wants to
b) Fred’s leaps get progressively smaller, so eventually he will grind to a halt.
Which is correct?
Everyone who enjoys mathematics will be able to pinpoint a time in their childhood that inspired them or particularly piqued their interest, for me it was Fred the lazy frog. I loved maths in school and was very quick at it, so often in lessons the teacher would hand my friends and me a book of puzzles and riddles to keep us occupied (thank you Ms Henderson.)
My gut reaction to the problem was (a), and this is the most common reaction of 16 year-olds that I now teach. It seems to make logical sense that if Fred is always moving forward – even if only a little bit – he can eventually reach the end of the pond, then the end of the field, then the end of the country. He has infinite jumps to use, after all! But, alas, I was wrong. Let’s have a look at the distance covered by Fred after his first ten jumps:
| Jump: | Distance (m): |
| 1 | 0.5 |
| 2 | 0.5 + 0.25 = 0.75 |
| 3 | 0.75 + 0.125 = 0.875 |
| 4 | 0.9375 |
| 5 | 0.96875 |
| 6 | 0.984375 |
| 7 | 0.9921875 |
| 8 | 0.99609375 |
| 9 | 0.998046875 |
| 10 | 0.9990234375 |
It seems that Fred is able to hop himself frustratingly close to 1 metre, without quite getting there. We say that there is a ‘limit’ of 1 metre, which actually means that neither statement (a) nor (b) above is quite correct. Fred is always moving forward, AND he will never reach a distance of 1m.
When I found this out in school, I was dumbfounded. How can this possibly be?! How are kids running around playing hockey on the field, or reading about the Russian revolution, or eating turkey twizzlers in the canteen, when there is a frog that can jumps forward ten billion billion billion times and never get past 1 metre. Stop everything!!
Here’s one way of showing it: start with a square, and then shade half of it, then a quarter, then an eighth, and carry on like this as long as you can manage:
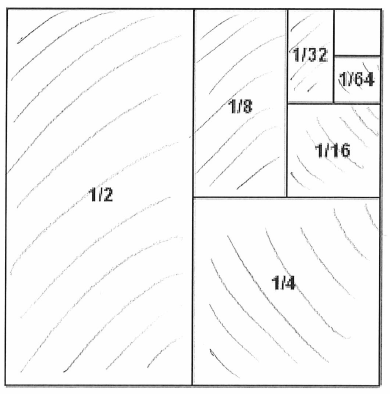
The left hand rectangle represents Fred’s first jump, the square in the bottom right his second jump (note that it is half the size of the previous rectangle) and so on.
This demonstrates the nature of a limit quite beautifully: it is quite clear that we are adding to the shaded area every time, but it is also clear that the entire square will never be fully shaded, even though we can get infinitesimally close. The sum total of Fred’s jumps tends to one metre.
To consider what’s going on here algebraically, please consider both Fred the lazy frog and his friend, Fran the feeble frog. Fran jumps under the exact same restrictions that Fred does, except that her first jump is only a quarter of a metre, followed by an eighth, a sixteenth, etc:
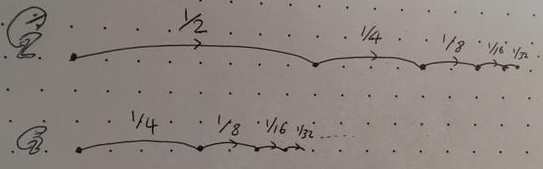
Hopefully it’s obvious that Fran will eventually jump half as far as Fred, because every one of her individual jumps is half the length of Fred’s corresponding jump. But closer inspection shows that Fran does in fact perform all of the same jumps as Fred, other than the original half metre jump:
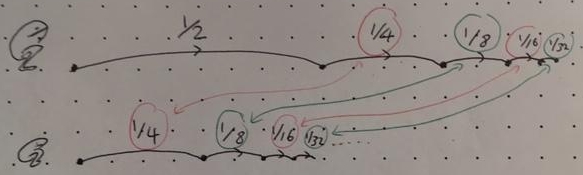
Written algebraically the above diagram looks like this:
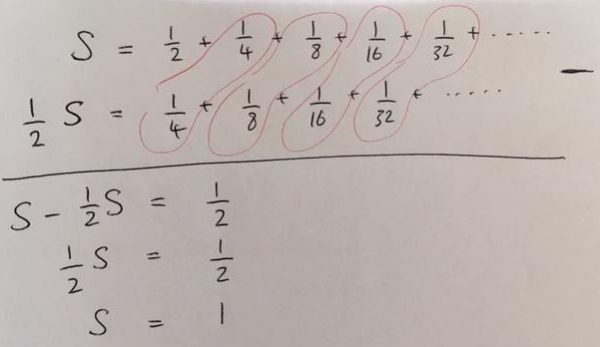
So that starting with the sum of Fred’s jumps (which I’ve called $S$) and subtracting the sum of Fran’s jumps (half of $S$) leaves half of $S$, which must be equal to a half. Doubling both sides of the equation tells us that $S = 1$, ie the sum of Fred’s jumps is 1, or rather the sum of Fred’s jumps tends to 1, as the number of jumps tends to infinity. The same logic can be applied for any sequence where the multiplying factor, or common ratio, is between -1 and 1.
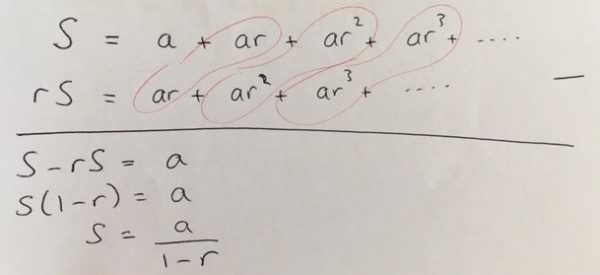
So that if Fred’s first jump of the day was 6 metres, but each jump is a quarter of the previous jump, the limit of his jumps would be $\frac{6}{1-0.25} = 8$ metres.
The fact that a half plus a quarter plus an eighth plus a sixteenth plus ….. tends to 1 is probably the best known limit in all of mathematics. It is such a well-known limit, in fact, that it has spawned a mathematical joke:
An infinite number of mathematicians walk into a bar. The first orders a half pint, the next orders a quarter pint, the next an eighth of a pint, the next a sixteenth of a pint…. The bartender stops them and pours a single pint.
This joke was demonstrated beautifully by the Aperiodical’s own Katie Steckles on popular TV quiz show QI (readers outside the UK: yes, it was very exciting to see a mathematician as special guest on one of the country’s favourite quiz shows.) Katie had prepared glasses sized in halving quantities, from a half-pint all the way down to a teeny 1/256th of a pint (that’s even smaller than the ones they have in Australia.)

These were then all emptied into a pint glass, which of course fit perfectly. In some versions of this joke the bartender is somewhat of a mathematical joker themself, telling the infinite queue of mathematicians: “Know your limits!” Sadly, this episode doesn’t appear to be available online any more.
Hopefully by now you are convinced that this infinite sum does indeed glean a finite result, having seen it pictorially, algebraically and, erm, fluid-ly. Like me, you may not be happy or satisfied with this result – indeed a member of my class once looked on the edge of tears during my lesson on the topic.
“Kyle”, they said “am I understanding this right – in any halving sequence, the sum of all the terms will never exceed, or even reach, twice the first term?”
“Indeed, that’s correct”, I replied.
“So, that’s the same as saying that the sum of all the terms after the first term will never reach the size of the first term?”
“Yep, that’s correct. It will get infinitesimally close, but never reach it.”
“That just makes me really sad about Fred the Frog”, the student sighed, clearly crushed.
“Why so?”
“Well, if he takes his first jump of the day and then realises he’s left something at home, he’d never be able to get back home to collect it.”
Anna Haensch –

Anna Haensch is a professor at Duquesne University in Pittsburgh, PA. She’s a number theorist, math blogger, and sometimes podcaster. She’s @extremefriday on Twitter.

For those who followed the Big Internet Math-Off 2018 edition, you maybe recall that Matt Parker wrote about the Machine Educable Naughts And Crosses Engine (MENACE) which, built from matchboxes and marbles, uses Artificial Intelligence to learn how to win Naughts and Crosses…or Tic-Tac-Toe depending on which side of the Atlantic you’re on. This bureau you see above is a lot like that one, except with (forgive me, Matt) a beautifully heightened design aesthetic. Following the original design by the WWII British code breaker Donald Michie, the French artist Julien Prévieux designed the sleek and beautiful MENACE2 above.
If you already know all about MENACE, great. This post is about building a bigger better ultra-turbo-mega-MENACE, so don’t go anywhere. If you don’t know about MENACE yet, then let me quickly tell you a bit about it. Each box in the machine represents a current state of game play (if you look closely at the picture below, you will see that each little drawer has a partially filled out board drawn on it). Each drawer is filled with different colored marbles, where the color indicates where on the board the machine should move next. As the game goes on, the marbles are removed from the boxes and placed on the table. In the end, if the machine loses, the marbles are discarded, thus teaching the machine not to play that sequence of moves again. And if the machine wins or draws, the beads are put back in, plus more bonus beads of the same color to reinforce the behavior. This type of machine learning is called Reinforcement Learning.

Reading about this machine, I was reminded of a wonderful talk I saw by Ben Orlin at the JMM this year, where he taught the rules of Ultimate Tic-Tac-Toe. The idea of U-triple-T is that you have a maxi Tic-Tac-Toe board filled with mini Tic-Tac-Toe boards, and you want to win the maxi-game by winning the mini-games. The rules are (at first) quite simple. The first player chooses any mini-board, and places an “X” in one of the nine spots of the mini-board. The spot she chose on the mini-board, dictates which mini-board the second player with take her move in. So if player 1 places an “X” in the top left corner of the top right mini-board, then player 2 will place an “O” somewhere in the top-left mini-board, and so on. It ends up looking something like this.
A mini board is won in the traditional way, and then the ultimate winner is the one who wins three mini-boards in a row. Things get a bit complicated when mini-boards have been closed out, but I’ll let Orlin explain that in his excellent blog post on the topic. So this altogether made me wonder about the feasibility of building a Freaking Ultimate Robot Naughts And Crosses Engine (FURNACE). And as it turns out, such a thing already exists, in fact the gif you see above is from Ofek Gila’s online FURNACE. What’s interesting is that MENACE and FURNACE require very different approaches in AI. Since Tic-Tac-Toe is a relatively simple game, there are only 304 admissible board configurations. Figuring out how we get to that number is already a worthy exercise in combinatorics. To begin, there are
\[ 3^9 = 19,\!683 \]
many ways to fill a board with “X” or “O” or blanks. We have to make sure the number of “X” and “O” only differ by one, and we have to remove all boards that are built by augmenting boards that have already been won. Finally, we have to divide out by the symmetries of the board. This leaves us with only 304 possibilities, and so it’s possible for MENACE to learn by going all the way through the game a few times, sort of like a depth-first search. On the other hand, FURNACE has far too many game configurations to make a depth-first search feasible. To count the total number of configurations, we start with
\[ 3^{81} = 443,\!426,\!488,\!243,\!037,\!769,\!948,\!249,\!630,\!619,\!149,\!892,\!803 \]
possible ways to fill the grid with “X” or “O” or blank, and then start subtracting and dividing. The symmetries, Whitney George and Janine E. Janoski showed that equivalent games of UTTT can be explained by group action by the dihedral group. That still leaves all of the augmented winning boards to deal with, and all of the boards that have the wrong number of “X” and “O.” Not only that, we also have to remove all boards that don’t follow the correct sequential-play rules. But that still leaves a bajillion or so possibilities (actual solution left as an exercise). With all of these possible board states, even a minimax decision rule can’t gain much traction, since it’s hard to define a function to quantify how much better one player is doing than another. The FURNACE you see above, which is remarkably quick, was built using a Monte Carlo Tree Search, and you can read all about FURNACE above on Gila’s blog, including the code to build your own!
So, which bit of maths do you want to win? Vote now!
Match 16: Group 4 - Kyle D Evans vs Anna Haensch
- Anna with FURNACE
- (51%, 114 Votes)
- Kyle with Fred the lazy frog
- (49%, 109 Votes)
Total Voters: 223
This poll is closed.
The poll closes at 9am BST on the 17th. Whoever wins the most votes will win the match, and once the group stages are over, the number of wins will determine who goes through to the semi-final.
Come back tomorrow for our eighteenth match of the group stages, featuring Alex Corner and Alaric Stephen. Or check out the announcement post for your follow-along wall chart!
Hi!
Something seems to be broken with the voting system.
According to the results shown, Anna has 17 votes out of 8 total, which gives her 213%, while Kyle has 5 out of 8, which is 65%.