
Here’s the sixth match in Round 1 of The Big Internet Math-Off. Today, we’re pitting Matt Parker against Matthew Scroggs.
Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!
Matt Parker – Machine Learning with Beads in Matchboxes
 Matt Parker is a standup mathematician with a lot of jobs. He’s one third of the scientific comedy group Festival of the Spoken Nerd, author of the book Things to Make and Do in the 4th Dimension, he sells mathematical toys at Maths Gear, he frequently features on Numberphile, and he does stuff for schools through Think Maths. You can find him on Twitter at @standupmaths, on YouTube, or at standupmaths.com.
Matt Parker is a standup mathematician with a lot of jobs. He’s one third of the scientific comedy group Festival of the Spoken Nerd, author of the book Things to Make and Do in the 4th Dimension, he sells mathematical toys at Maths Gear, he frequently features on Numberphile, and he does stuff for schools through Think Maths. You can find him on Twitter at @standupmaths, on YouTube, or at standupmaths.com.
Donald Michie was a cryptography and artificial intelligence expert who worked at Bletchley Park with Alan Turing during the Second World War. In 1961 he built an analogue machine which could learn to play nights and crosses: the Machine Educable Noughts And Crosses Engine (MENACE).
(Umpire’s note: Matt is either turning his competitor’s strong maths-fu against him, or has got confused about which Matt he is. I’ll allow it.)
In 2016 the UCL mathematician Matthew Scroggs re-built MENACE. It consists of 304 matchboxes: one for each of the unique game-states of naughts and crosses the player who goes first can possibly face during a game. In each matchbox are colours beads which correspond to the moves the player can make.
MENACE starts off playing randomly, but by rewarding winning moves with more beads of those colours, and punishing losing by removing beads it can learn to play an optimal strategy over the course of a few hundred games.
We took MENACE to the 2017 Manchester Science Festival to let it play against the public. Over the course of each davit would learn to play perfect naughts and crosses. My favourite moment was when a member of the public complained that MENACE could not possibly be an example of machine learning because it was too easy to understand. Apparently something is only machine learning if it is complicated!
There’s more information in Scroggs’s article about MENACE on his blog.
Matthew Scroggs – Mathsteroids
 Matthew Scroggs is a PhD student at University College London, and one of the co-editors of Chalkdust Magazine. You can find him on Twitter at @mscroggs, or on mscroggs.co.uk.
Matthew Scroggs is a PhD student at University College London, and one of the co-editors of Chalkdust Magazine. You can find him on Twitter at @mscroggs, or on mscroggs.co.uk.
A map projection is a way of representing the surface of a sphere, such as the Earth, on a flat surface. There is no way to represent all the features of a sphere on a flat surface, so if you want a map that shows a certain feature of the world, then you map will have to lose some other feature of the world in return.
To show you what different map projections do to a sphere, I have created a version of the game Asteroids on a sphere. I call it Mathsteroids. You can play it here, or follow the links below to play on specific projections.
Mercator projection
The most commonly used map projection is the Mercator projection, invented by Gerardus Mercator in 1569. The Mercator projection preserves angles: if two straight lines meet at an angle \(\theta\) on a sphere, then they will also meet at an angle \(\theta\) on the map. Keeping the angles the same, however, will cause the straight lines to no longer appear straight on the map, and the size of the same object in two different place to be very different.
The angle preserving property means that lines on a constant bearing (eg 030° from North) will appear straight on the map. These constant bearing lines are not actually straight lines on the sphere, but when your ship is already being buffeted about by the wind, the waves, and the whims of drunken sailors, a reasonably straight line is the best you can expect.
The picture below shows what three ships travelling in straight lines on the sphere look like on a Mercator projection.
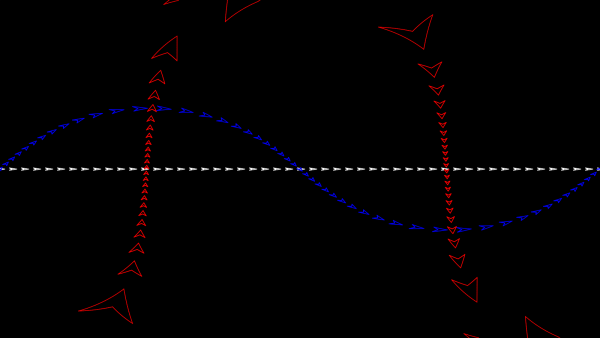
To fully experience the Mercator projection, you can play Mathsteroids in Mercator projection mode here. Try flying North to see your spaceship become huge and distorted.
Gall–Peters projection
The Gall–Peters projection (named after James Gall and Arno Peters) is an area-preserving projection: objects on the map will have the same area as objects on the sphere, although the shape of the object on the projection can be very different to its shape on the sphere.
The picture below shows what three spaceships travelling in straight lines on a sphere look like on the Gall–Peters projection.
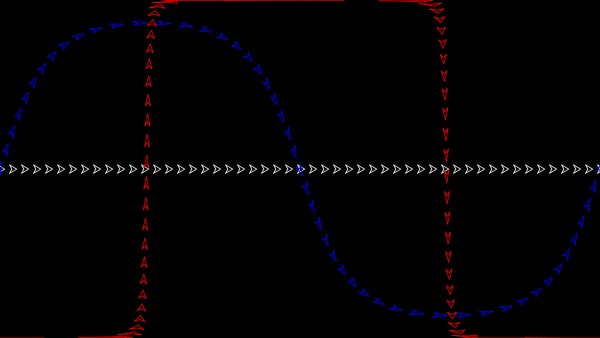
You can play Mathsteroids in Gall–Peters projection mode here. I find this one much harder to play than the Mercator projection, as the direction you’re travelling changes in a strange way as you move.
Azimuthal projection
An azimuthal projection makes a map on which the directions from the centre point to other points on the map are the same as the directions on the sphere. A map like this could be useful if, for example, you’re a radio operator and need to quickly see which direction you should point your aerial to communicate with other points on the map.
The azimuthal projection I’ve used in Mathsteroids also preserves distances: the distance from the centre to the another points on the map is proportional to the actual distance on the sphere. This projection is used as the emblem of the UN.

The emblem of the UN
The picture below shows three straight lines on this projection. You can play Mathsteroids in azimuthal mode here.
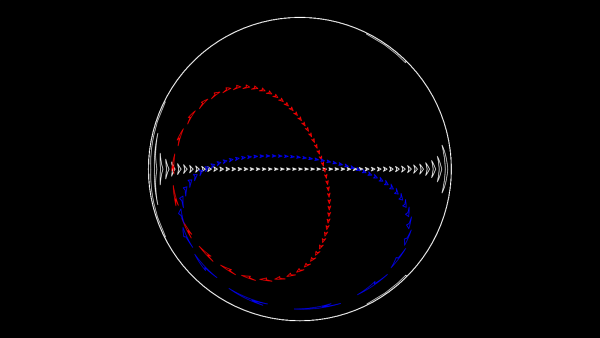
Craig retroazimuthal projection
A retroazimuthal projection makes a map on which the directions to the centre point from other points on the map are the same as the directions on the sphere. If you’re thinking that this is the same as the azimuthal projection, then you’re too used to doing geometry on flat surfaces: on a sphere, the sum of the angles in a triangle depends on the size of the triangle, so the directions from A to B and from B to A aren’t as closely related as you would expect.
The Craig retroazimuthal projection was invented by James Ireland Craig in 1909. He used Mecca as his centre point to make a map that shows muslims across the world which direction they should face to pray.
The picture below shows what three spaceships travelling in a straight lines on a sphere looks like on this projection.
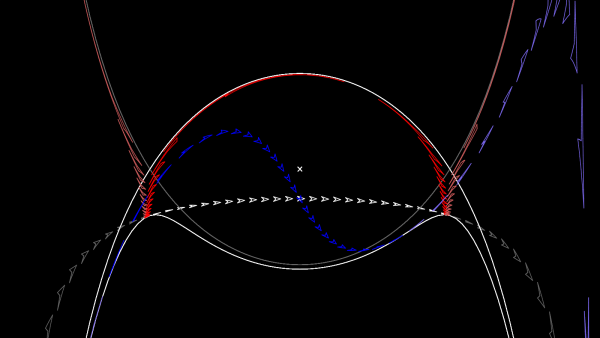
You can play Mathsteroids in Craig retroazimuthal mode here to explore the projection yourself. This is perhaps the hardest of all to play, as (a) two different parts of the sphere overlap on the map, and (b) the map is actually infinitely tall, so quite a bit of it is off the edge of the visible game area.
Stereographic projection
The final projection I’d like to show you is the stereographic projection.
Imagine that a sphere is sitting on a 2D plane. Take a point on the sphere. Imagine a straight line through this point and the point at the top of the sphere. The point where this line meets the 2D plane is stereographic projection of the point on the sphere.
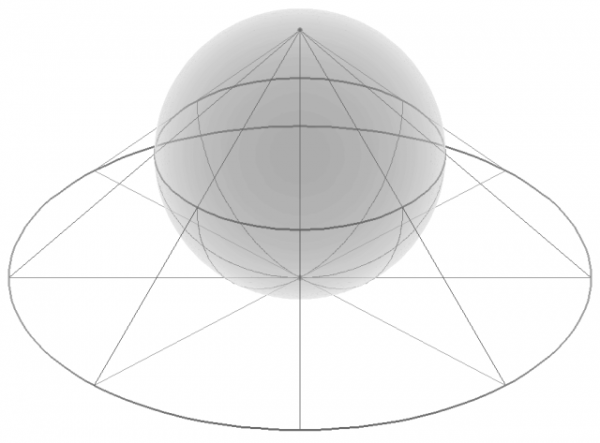
The stereographic projection
This projection (backwards) can be used to represent the every complex number as a point on a sphere: this is called the Riemann sphere.
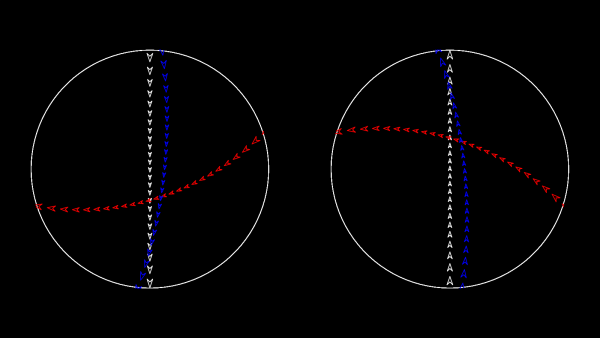
To make Mathseteroids playable after this projection, I split the sphere into 2 hemisphere and projected each seperately to give two circles. You can play Mathsteroids in stereographic projection mode here. Three spaceships travelling in straight lines on this projection are shown below.
… and if you still don’t like map projections, you can still enjoy playing Mathsteroids on an old fashioned torus. Or on a Klein bottle or the real projective plane. Don’t forget to take a short break from playing to come back here and vote.
So, which bit of maths has tickled your fancy the most? Vote now!
Round 1 match 6 - Parker v Scroggs
- Matt Parker with Machine learning using beads in matchboxes
- (64%, 364 Votes)
- Matthew Scroggs with Mathsteroids
- (36%, 208 Votes)
Total Voters: 572
This poll is closed.
The poll closes at 9am BST on the 8th. Whoever wins the most votes will get the chance to tell us about more fun maths in round 2.
Come back tomorrow for our seventh match in round 1, pitting Jim Propp against Zoe Griffiths, or check out the announcement post for your follow-along wall chart!
One cool fact about the spherical projections is that they usually have their counterparts in hyperbolic geometry. For example, the famous Poincaré ball model is basically the stereographic projection of the Minkowski hyperboloid, and the less known band model is the hyperbolic version of the Mercator projection.
There are several game projects with experiment with non-Euclidean geometry and its projections. Our HyperRogue has a large selection of projections and a large selection of geometries; the standard game is a bit like Chess, but it also has a real-time shooting mode. MagicTile is a Rubik cube-like puzzle with many projections and geometries.