Tim has previously written guest posts here about tiling by tricurves, and is now looking at ways of tiling with other shapes.

In an earlier post elsewhere I covered some basic arc-sided shapes that tile by themselves. Lately I’ve been playing with groups of curved tiling shapes, asking a question common for me: how to get the most play value as an open-ended puzzle? This means getting the most interesting possibilities from the simplest set. “Interesting” includes variety, complexity, challenge and aesthetic appeal. “Simplest” covers not only size of set and the shapes, but also the least total information needed to describe or construct the shapes.

My simple approach here is to start out with one interesting main shape and see what other (minor) shapes are needed to fill in the gaps, by trial and error; then try to refine and optimize that set to make it, in a sense, efficient.

For this post I’ve avoided the frameworks of the self-tiling regular triangles, squares and hexagons. Let’s look at two main shapes: the first is based on the pentagon; the second is a tricurve.

Using Pentagons

The regular pentagon of course can’t tile by itself. The set of tiles needed to help tile the plane with regular pentagons is well known. But let’s replace the sides of a regular pentagon with concave arcs of 72°.  We can lay these out in various ways to get different types of gaps, as shown here:

Note in many cases a point is hitting midpoint on a neighboring arc. Many of these gaps can be filled with simple lens shapes of 36°, 72° and 108°:

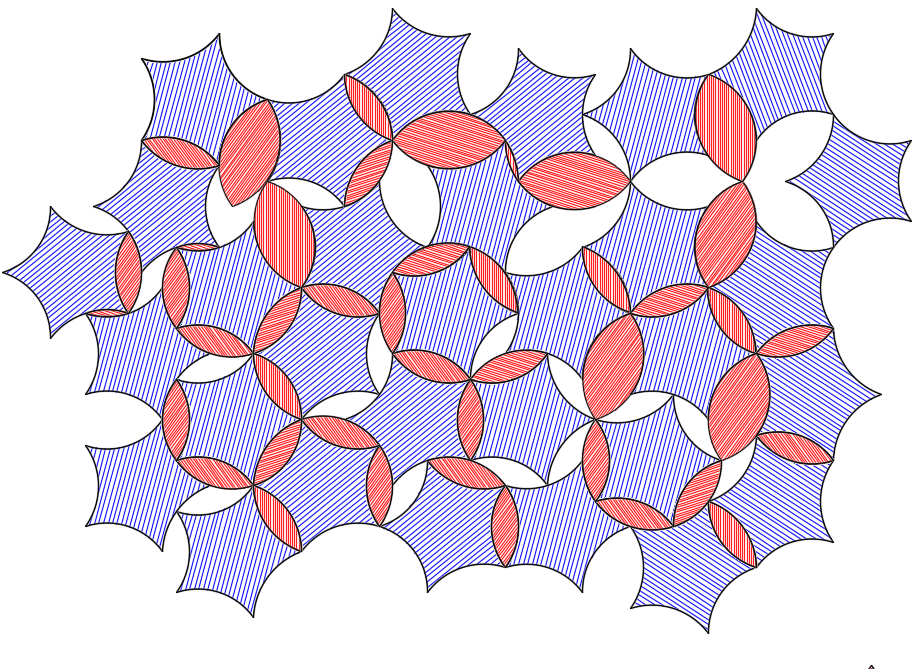
The remaining gaps need to be filled with partial lenses: 72° or 108° lens with one or more chunks gone. To fill the remaining gaps as is would require at least four more shapes. But we can reduce this number by backing up and combining the smaller tiles. If we start with the 36° lens and add a 4-side concave diamond (with corners of 36° and 144°, and 36° concave arcs) we can get the 72° lens and any partial 72° lens. In order to make the 108° lens we need to use another concave diamond, with corner angles of 72° and 108°.  This also lets us fill out the end of the elongated 108° lens shape.

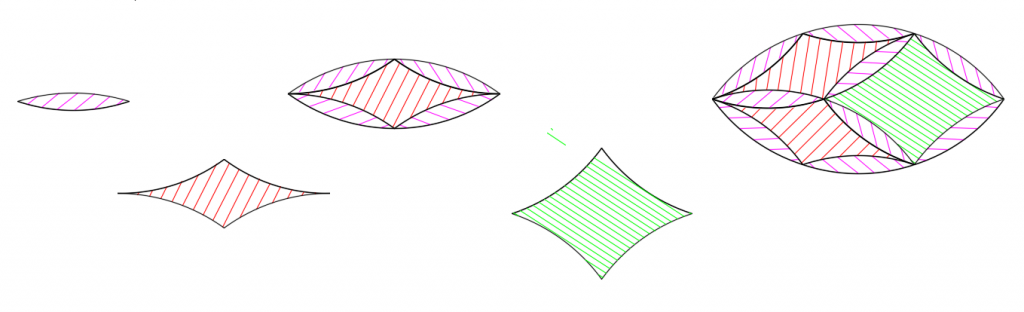
So now the part count is four shapes (above): one major and three minor, and these let us fill the gaps:

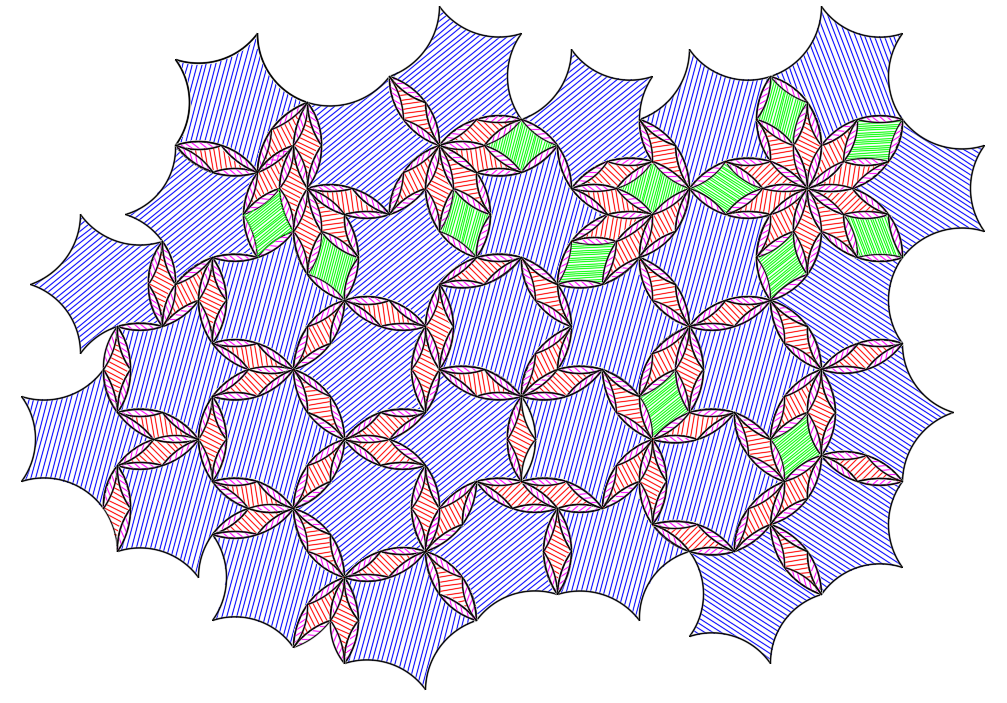
If this were a real puzzle we would probably complain about the large number of little 36° lens pieces. Can we use less of these? The 36° lens only needs to be separate from the 4-concave diamonds in the cases where the lenses would overlap. We can permanently attach two of the 36° lenses to the thin diamond; and attach three 36° lenses to the wide diamond. So now our minor shapes look like this:

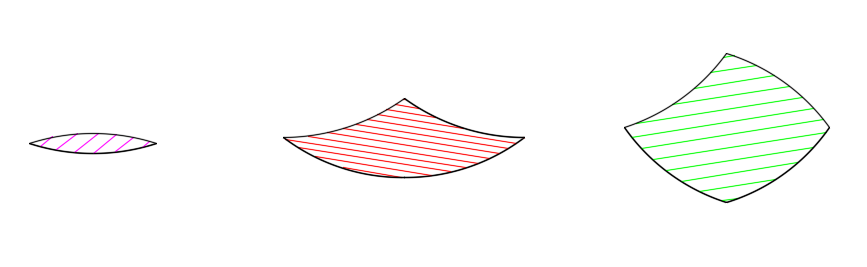
 and the tiling looks like this:

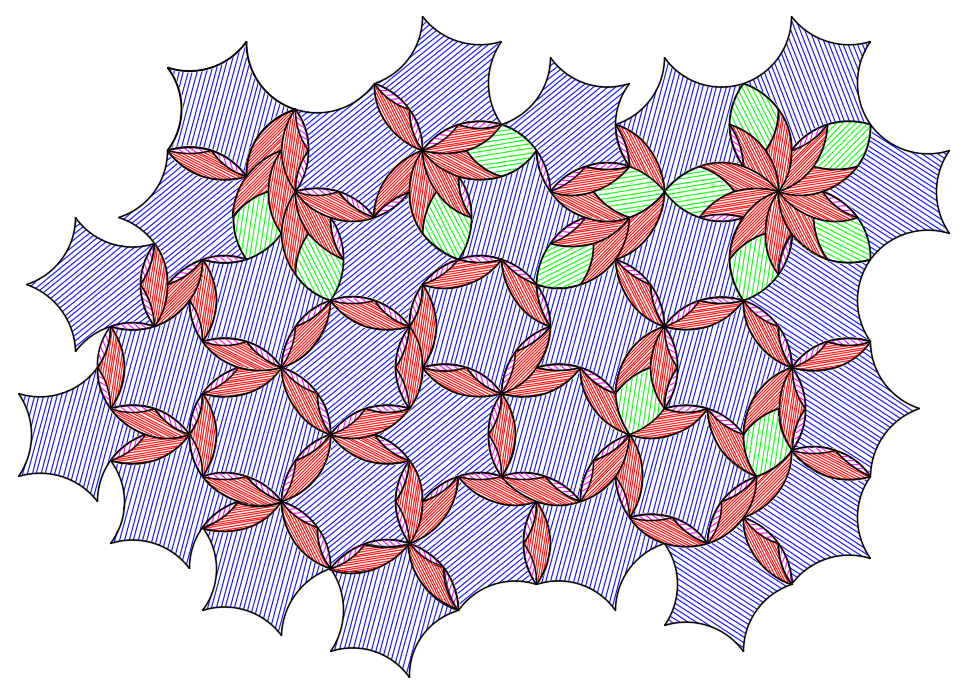
This set of tiles seems a reasonable solution (although other similar sets are possible). Now rather than simply filling gaps, we can start exploring various tilings:

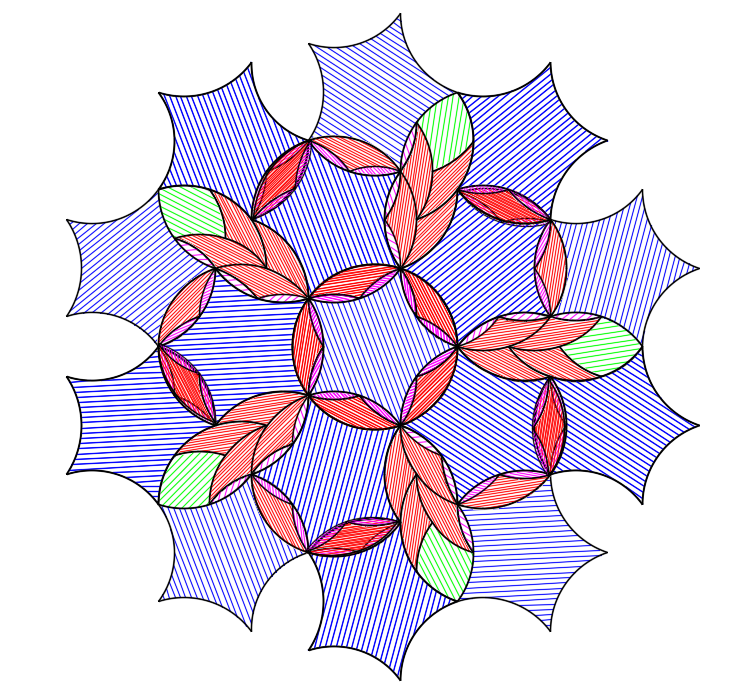
Using Tricurves

The second main shape is a 36°-72°-108° tricurve, which is quite different. The tricurve already has great flexibility for tiling by itself periodically, non-periodically, and radially (as shown in previous post). So any additional parts should add to the possibilities – and it doesn’t take much. Even adding a single 36° or 72° lens at the center of a radial tiling opens many possibilities:

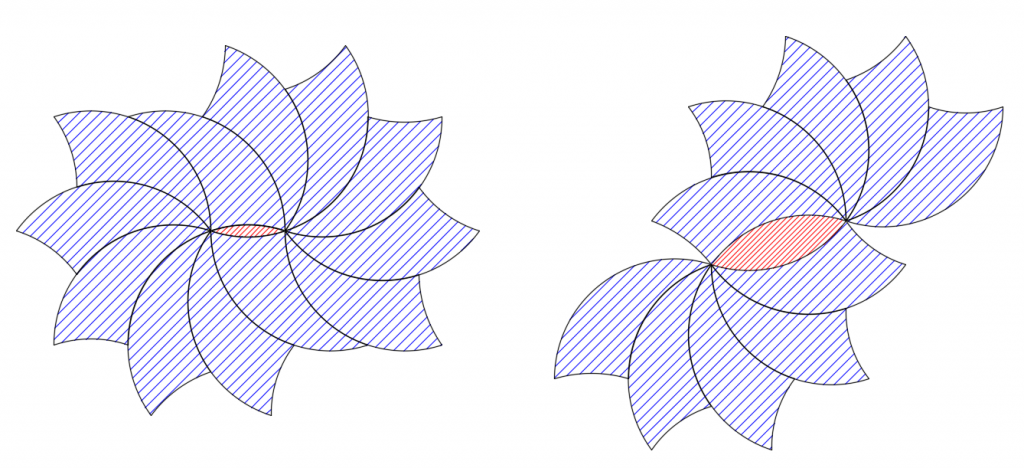
Since the underlying geometry is similar let’s start out with our original three minor shapes: the 36° lens and the two 4-sided concave diamonds. These let us create a very wide range of tilings:

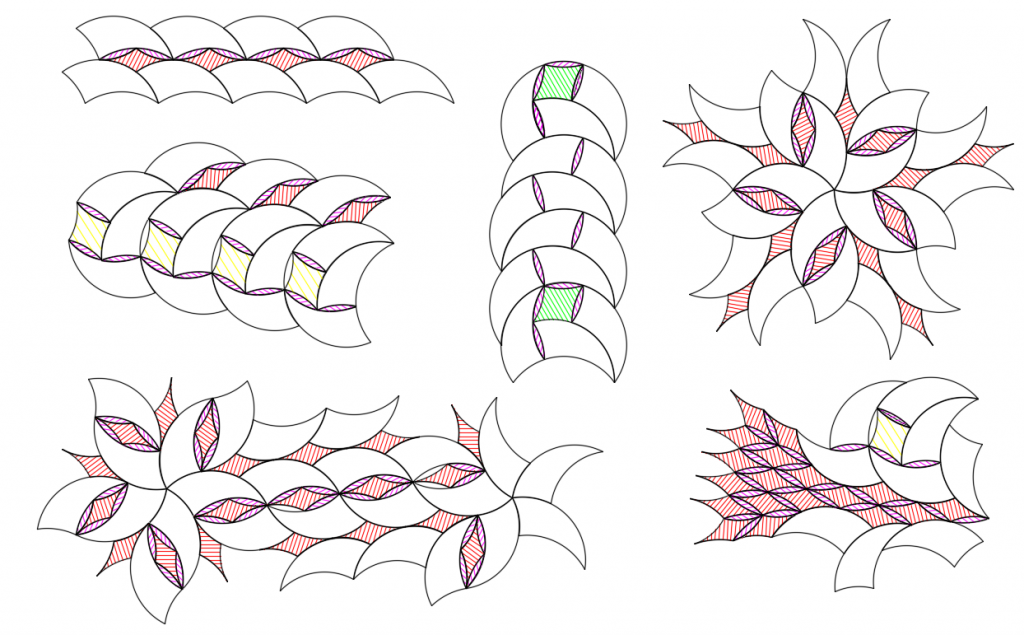
Some of these patterns are of course not sustainable for tiling the plane. The additional complexity allowed comes partly from a means to fill gaps between adjoining convex sides or concave sides. Each of the three minor shapes by itself can add to tricurve tiling complexity, as can the use of any two of the minor shapes. Also the minor shapes can tile without the main shape –which the pentagon minor shapes can’t do (Why not?).  

Because of the ways a tricurve can tile with itself, there are many more opportunities for odd-shaped gaps that can’t be covered with the three minor shapes. With the tricurve the tiling is much more open-ended that with the pentagon above. There are no doubt various other minor shapes that could be added to fill gaps, but we’ll stick with these three for now. This whole set is interesting since it consists partly of nested lens shapes:

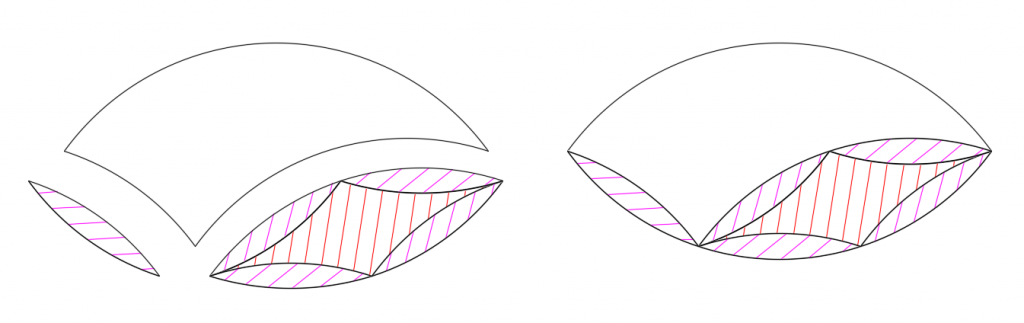
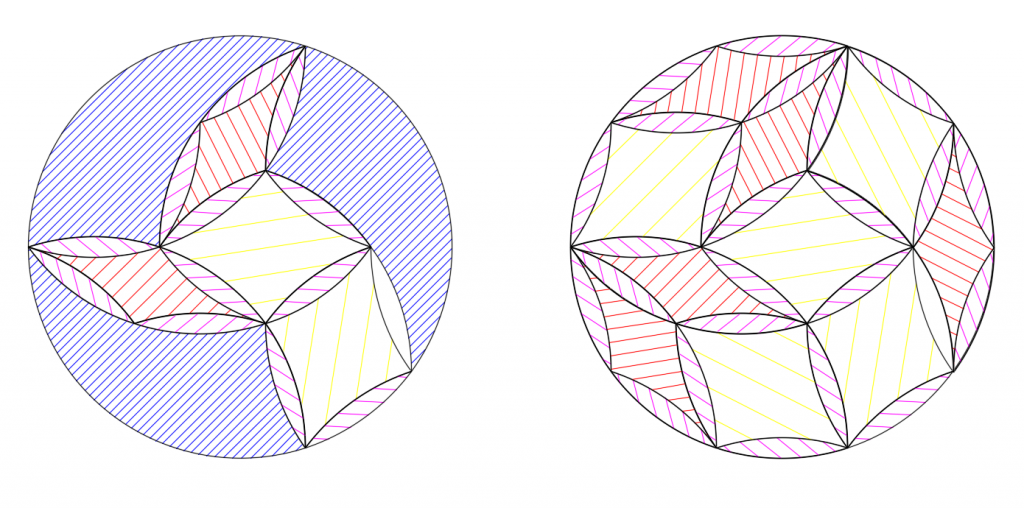
Also the tricurves—or either of the concave-diamond shapes for that matter—can make a circular hole, which can be filled with a circle made of the set or just the minor pieces:

Thoughts on tiling set design

Designing a small tiling set involves making tradeoffs between shape complexity, part count, and aesthetic appeal. In both shape sets, part of the complexity of the final tiling is in the use of the arcs. There is a pattern of arcs interwoven with the pattern of shapes; this may be seen as full or partial circles, or in the patterns of the arcs as they branch and connect. Also we can choose shapes to make tiling (as a puzzle) more challenging; for instance, if we modify the concave-sided pentagon so one of its sides is a convex arc, tiling will require more thought and thus be more interesting.

Both main shapes above are of course compatible with the minor shapes. This is not surprising since all the shapes incorporated 36 and 72 angles. The underlying diamonds with corners of 36° and 144°, or 72° and 108°, are two rhombus shapes used in a version of the Penrose tiles.

We could of course reduce these sets and their tilings by replacing all 36° arcs with straight lines (facets). The 36° lens shape disappears, reducing the set part count and the count of the lens pieces in the tiling.

Surprisingly, this reduction by faceting makes some things a little more complex. The larger arcs of the two main shapes would now be more complex to describe and construct. Since we sometimes connected at the midpoint of pentagon’s concave side, we’ll need to describe the shape as having ten faceted sides. Likewise, to keep the effect of the concavity of the smallest arc, the faceted equivalent of the tricurve needs 12 sides and four unique angles –whereas the much simpler tricurve can be described with two angles (36° and 72° – the 108° is the simple sum and redundant).

Compared to structurally equivalent tilings with faceted tile shapes, the above arc-sided sets:

• have the additional part count of the 36° lens shape
• have more complex diamond shapes, due to their 36° arcs
• have main shapes that are simpler to describe and construct
• have the aesthetic appeal and interest of connected arcs; and
• overall provide more challenge and play value.

Further possible investigations:

What happens when we use both the concave pentagon and the tricurve as main shapes in the same set?

What other main shape would you try as a starting point?