For me, the above shape emerged when playing with a drawing compass. Of the two ancient tools, I preferred the compass over the straightedge. I was fascinated with the classical geometric constructions, the intersecting circles and arcs. As a simple personality test, preferring a compass over a straightedge might mean something: maybe roundabout-holistic-intuitive more than straightforward-linear-realistic. At any rate, the pursuit of curves eventually led me to this topic, but to explain I need to start with straight lines and triangles.
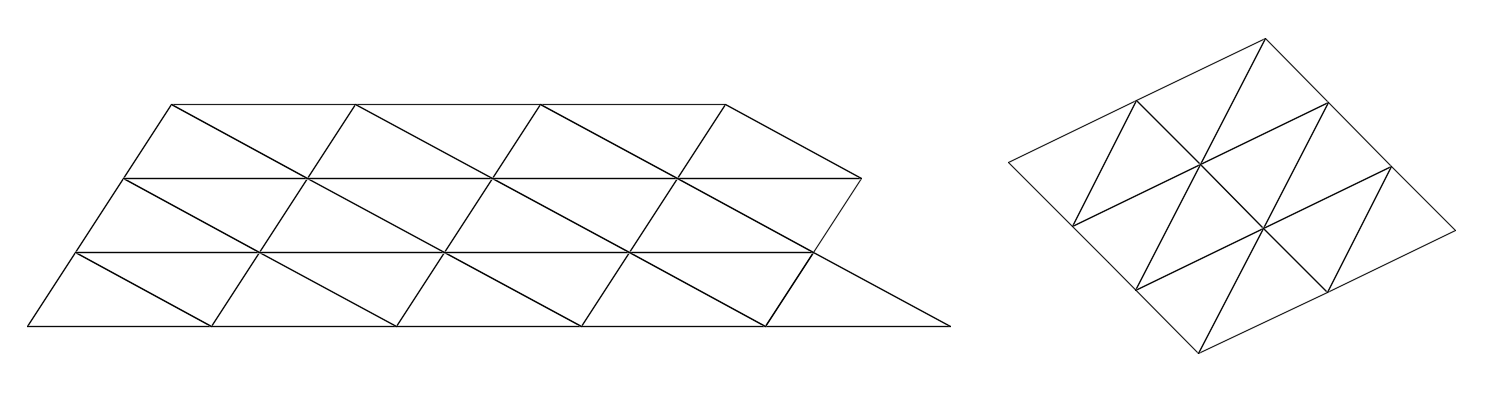
You can tile a plane with a repeated single triangle shape. But for most triangles you need to put same sides together, usually to group pairs of triangles into parallelograms, as shown above. You can’t just put any sides together. This of course reflects the Law of Sines, which says the side lengths are proportional to the sines of their opposite angles: you can’t get both the angles AND the side lengths in agreeable proportions.
But something unexpected happens when we add curves. For tiling we need equal amounts of concave and convex arc. The only way to do that is with two shorter concave sides joining a longer convex side, as shown below.
Building the Arcs
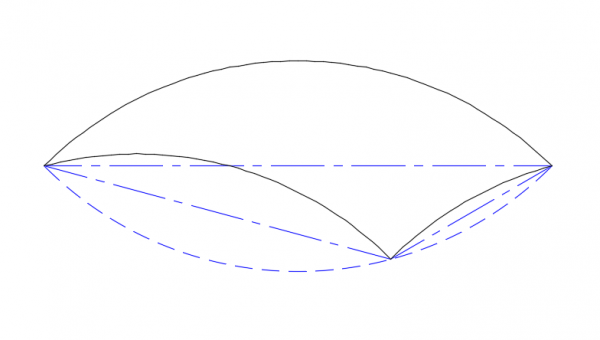
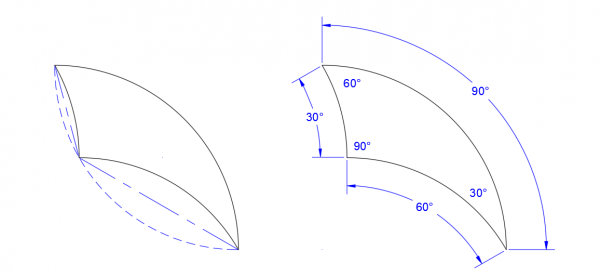
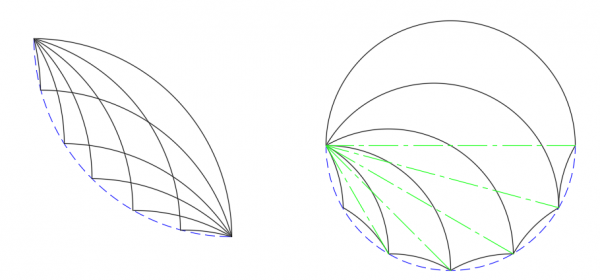
The tricurve starts with a simple arc: in this example, 90°. The arc is then mirrored about its endpoints to make a lens shape, and the new arc is divided into the two parts such as 30° and 60°. Each of these smaller arcs is in turn mirrored about its endpoints, forming the two concave portions of the tricurve. For any tricurve, the corner of the two smaller arcs falls on the reflection of the large arc.
The result is that each arc matches the angle of its corner opposite. The corner angle opposite the large arc, measured between the tangents at the arc ends, is always the supplement of the large arc; in this case of the large arc being 90°, the supplement is also 90°. Far from following the Law of Sines, in this case –and in all cases using 90° as the large arc—each corner angle is the same as its opposite arc. The convex arc angle is the sum of the two concave arc angles. The arc angles—not arc lengths per se—are of interest. The radius should be considered a unit length. As with a standard triangle, the three corner angles sum to 180°. This kind of shape has interesting properties by itself, but here we will focus on tiling.
For tiling with a normal triangle, the straight sides and corner angles can seem separate aspects: competing and related in a non-intuitive manner. But in a tricurve we have only angles of arcs and corners to consider. This type of shape is extremely favorable for tiling, both by itself and with related shapes.
Basic Tiling
Some tiling options are shown in the drawing below, made using the single 30-60-90 tricurve, with reflection allowed. This shows a mix of periodic, nonperiodic and radial tiling, with various interesting relationships and sub-patterns.
This raises many questions: How many tile orientations are there? Can you cover this with a checkerboard pattern? Do all the surrounded tiles have the same number of neighbors? As you add more tiles, how will you keep from getting stuck? What rules emerge?
Tiling with tricurves is partly a matter of filling inside corners, as shown below.
More Possibilities
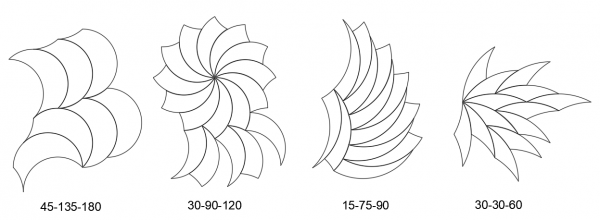
The tricurve relationships hold true for any large angle up to 180°, and for any ratio of the two smaller angles. Periodic tiling can be done with any angles, but for radial and more complex tiling the angles need to be divisors of 360°, usually multiples of 12° or 15°. The tricurve is best described with the arc angles in degrees (rather than the corner angles) in increasing value, such as the 30-60-90 above.
It also seems helpful to think in terms of corresponding ratios of the three arcs. In addition to the above ratio of 1:2:3, there is the simplest ratio of 1:1:2, and others such as 1:3:4 and 2:3:5. These ratios indicate how the tricurves will tile regardless of the actual angles used. The figures below show some families of tricurves.
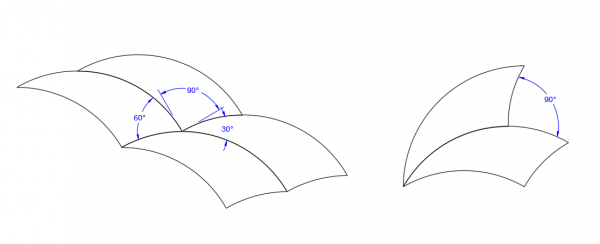
For any large arc, the opposite corner angle—the supplement of the arc angle—will still be an agreeable angle for tiling. For a given large arc, the opposite corner angle—and its orientation—will be constant regardless of the proportions of the two small arcs.
The figures below show a small sampling of the wide variety of tricurve shapes, arc ratios and tiling options. Note an asymmetrical shape gives more tiling options than a symmetrical one.
If we focus on periodic tiling we can get some changes of direction, with interesting sub-patterns, as shown below.
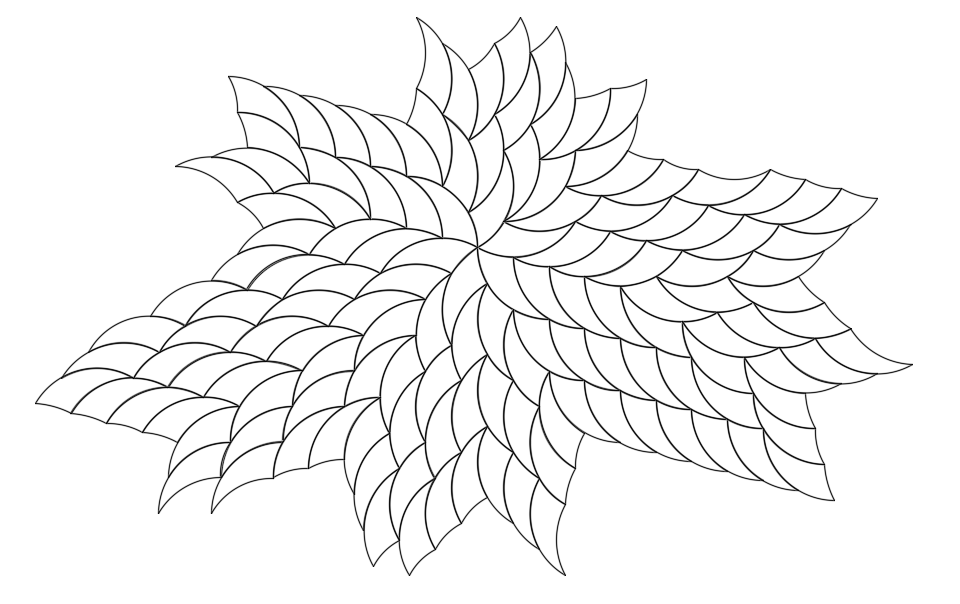
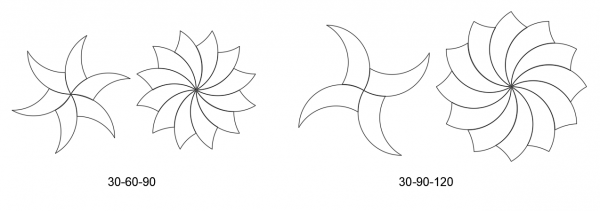
Tricurves make attractive radial patterns or polar arrays, as shown below. Even on the first, basic level they are eye-catching stars or flowers with a twist. But from a tiling standpoint these are just the start, with open inside corners to fill. Note the open corners are bounded by arcs of the same length. While either of the small angle corners can be at center, with the larger angle at center each open corner has more arc length available and can accommodate more filling options.
Any of these can be expanded outward in a variety of ways, as shown for one core star below.
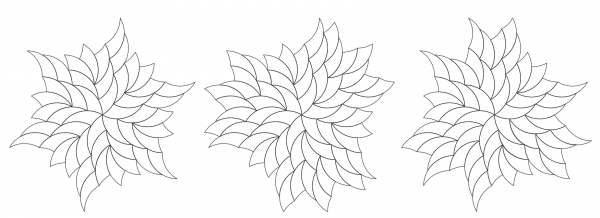
Adding Gaps or Other Shapes
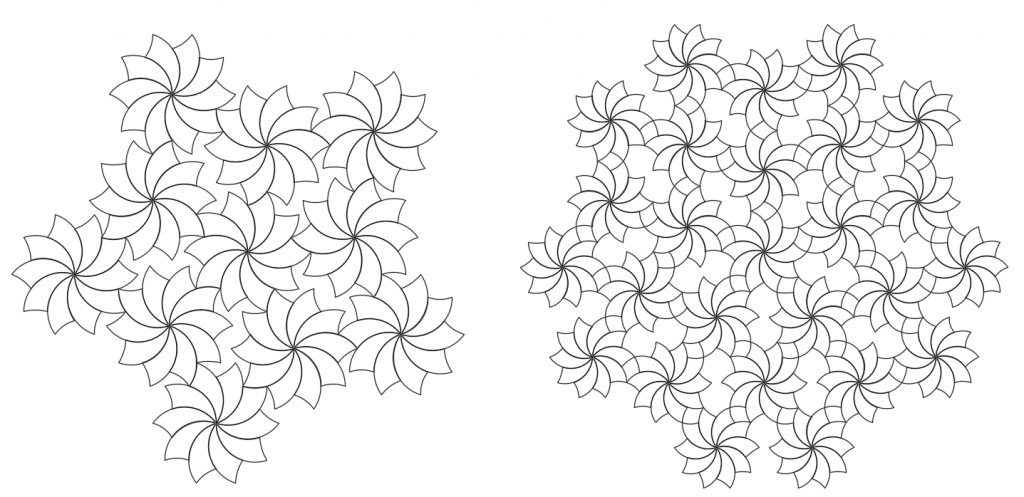
The ease of fitting extends beyond one-shape tiling. If we treat two or more identical tricurves as a group, we can make patterns with these groups. The gaps between the groups are made up of (bordered by) the same arcs and the same or related angles. These gap shapes can be considered separate tiling shapes.
For instance, the patterns below use two adjoining tricurves treated as a single unit.
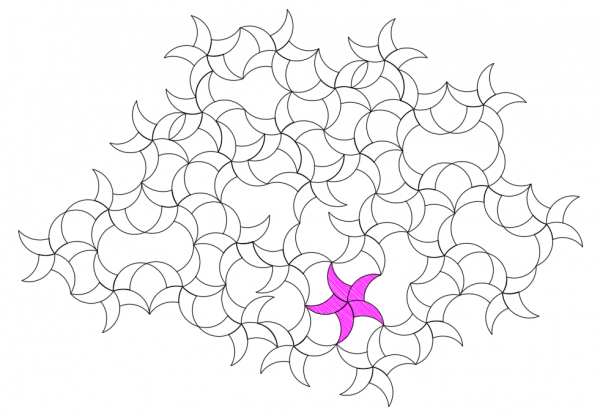
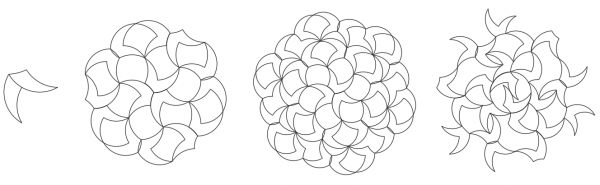
Some of the most intriguing patterns use stars or pinwheels, as shown in the examples below.
Some arrangements can be more freeform with a wide variety of space shapes, as shown below.
Going Further
Please try out and explore these ideas, and share what you find!
For background on tricurves, including properties of the shape itself, see National Curve Bank site and paper.
For more examples of tiling, see Paul Bourke’s site.
For a discussion of tiling with curve-sided shapes in general, see MathBlog post.
For a wooden tricurve puzzle, see Cherry Arbor Design.




Love this post! Lovely and intriguing. If people want to start playing with these digitally, I did make a GeoGebra applet for it… https://www.geogebra.org/m/nfPX5bpw