Tim Lexen has written a series of posts on the topic of Tricurves: Bending the Law of Sines, Combining Tricurves and Phantom Tiling. In this latest post, Tim has been working with our own Katie Steckles to turn Tricurves into real objects to play with.

When you discover an interesting mathematical shape or object, there’s a strong instinct to play with it – maybe by drawing sketches and doodles to test the limits of the idea. But in the case of Tricurves, drawing an accurate shape takes a little time, and it doesn’t lend itself well to idle experimentation.
Producing a physical version of a shape, in enough quantity to allow for experimentation, makes it much more tangible. In our own respective locations, we’ve each made use of laser cutting facilities to produce wooden Tricurve tiles to play with, and we encourage you to join in.
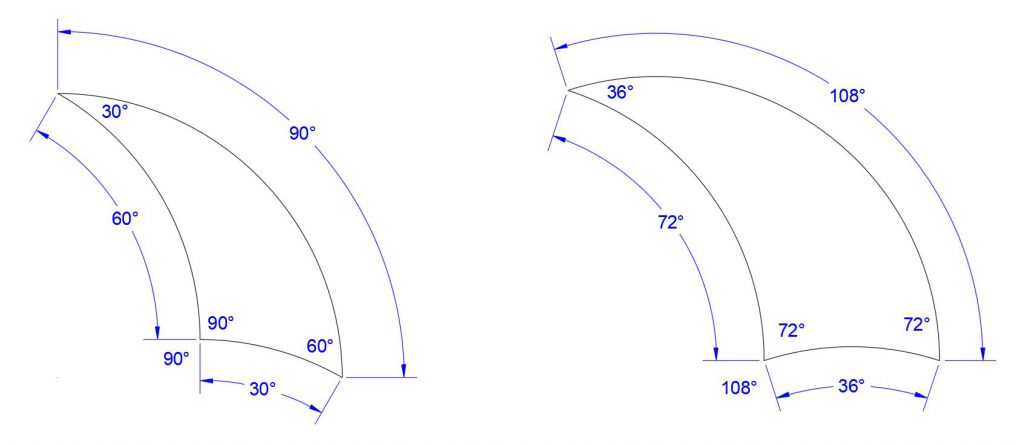
For simplicity, we’ve limited our real-world tiling adventures to two Tricurve shapes that seem the most popular and interesting: 30-60-90 and 36-72-108. As a star or flower pattern at the center of a design, the 36-72-108 makes 5- and 10-fold symmetry, and the 30-60-90 gives 6- and 12-fold radial symmetry.
If you have access to a laser cutter (or a vinyl cutter/plotter), this is a great way to create physical tiles to play with. We’ve made a few options, including a large pile of tiles from cheap 3mm MDF to allow them to be easily played with in the pub, some from 1/8 inch birch ply for a nicer finish, and a set in clear acrylic which looks great on a coloured background.

30-60-90 tiles in MDF 
30-60-90 tiles in acrylic
The cutting files can be downloaded below, in SVG (Scalable Vector Graphics) format. If you would like to make your own tilings on a computer, these files can also be edited using InkScape or similar vector graphics software, so you can manipulate the tiles and create layouts.
Hand-cut tiles
If you don’t have any way to get access to serious laser-based cutting equipment, you might prefer to print a sheet of tricurve tiles onto thick card or posterboard and cut them out by hand. Some useful PDF files for this can be downloaded below. This works best with heavier paper, and it may help to use at least a light adhesive to keep pieces in place.
Tiling Patterns
To give you some inspiration, here are some of the shapes we’ve successfully made – with and without allowing gaps between pieces.
Tracing Tricurves

If you’d like to create drawings of tricurve tilings, one way might be to use a single laser cut/hand cut tile and trace around it as a positive template. This can be used for some basic layout of small tiling patterns, but from what we’ve found, it’s not satisfactory for generating good tiling over a large area. It’s hard to extend the vertices outward, hard to line up arcs and vertices, and easy to be a few degrees off. Errors in alignment are often noticed only after more shapes are drawn.

More importantly, by tracing you’re not merely scaling the shape up by the offset of the pen or pencil tip – the offset increases the radius of the large convex arc but decreases the radii of the two smaller concave arcs. If you use a negative (hole) template, the same thing happens but in the opposite direction. A sharp pencil (or well-extended propelling pencil, or very fine-tipped pen) might allow you to get close enough to reduce this effect.
Further Thoughts
It might be interesting to see how tricurve tilings can be coloured, and there are plans to use some woodstain to make the MDF pieces four different colours for experimentation purposes. Katie suggests she’ll also keep working on electronic versions, using the SVG versions of the tiling pieces – potentially creating wallpaper or background images, and exploring the possibilities.
We hope you enjoy making and playing with these shapes! What designs and games can you invent? Experiment!







I really like these. The 5 and 10 fold symmetry version, reminds me of a shape that I made up in VectorEngineer Drawing but instead of curves I used straight lines – 9 in total. I have been meaning to get it on my blog for sometime. I think it works the same way.
Yes tricurves can often be replaced with faceted figures, as is done in designs such as the “bent wedge”, “versa-tile”, and the shapes of Paul Gailiunas. This is possible when the tricurve arcs are in some integer ratio such as 1:2:3 or 1:3:4. However note that any tricurve can always tile at least periodically: that is, for any arc angles and any ratio of arcs. Also the tricurve has some interesting aspects — such as its enclosed area; or phantoms (see other Aperiodical post “Phantom Tiling”) — not found with the faceted shapes.