In July, guest author Tim Lexen wrote about his discovery of the tricurve, a shape made of arcs that has some interesting properties. He’s written a follow-up in which he explores them further. For a discussion of tiling with curve-sided shapes in general, see Tim’s MathBlog post.
Tricurves can be combined when the large, convex arc of one fills a concave space of another. A tricurve can be thought of as a shape that fills a concave arc with two smaller arcs of the same total length. In each case the new arcs stay within the boundaries of the original structure: touching the same bounding arc. This could go on repeatedly (see below) but we’ll focus here on joining two tricurves. Like the tricurves, assuming agreeable angles, the combined shape will often be able to tile the plane periodically, non-periodically, and radially with itself and related shapes.
On the larger tricurve, we’ll be filling the larger of its concave arcs. The new combined shape will have three concave arcs; if these three arcs were all different, it would be difficult to tile with that shape. So here we’ll look at cases where two of the three arcs are the same: one from each of the two tricurves. As we’ll see, there are two possible arrangements: same concave arcs together, and same concave arcs opposite.
Same Concave Arcs Opposite
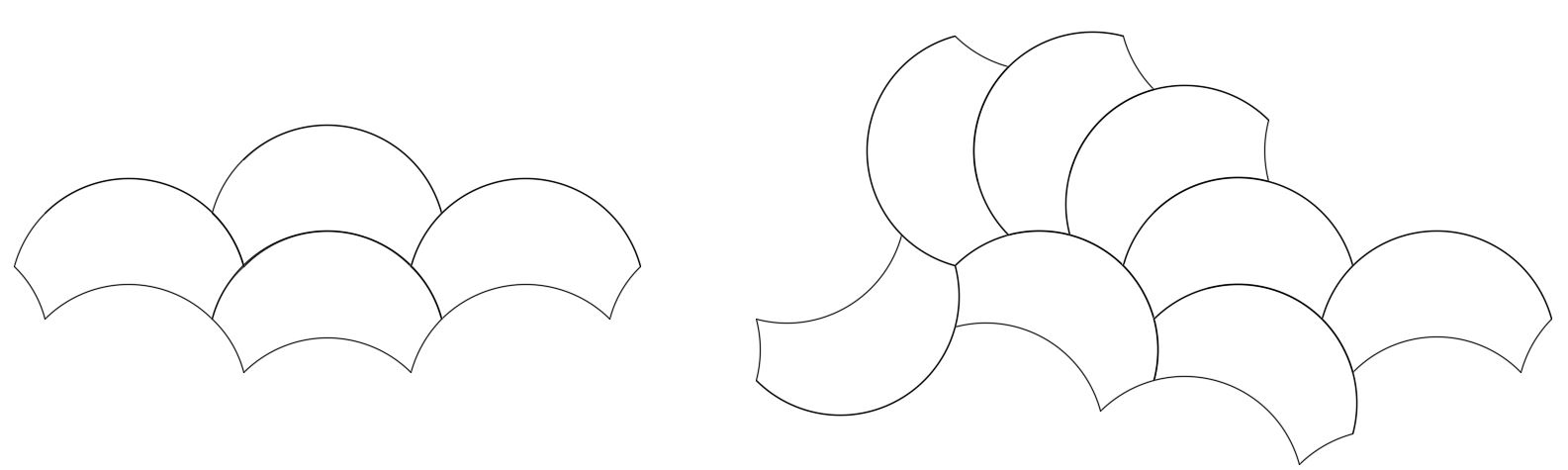
When we put same concave arcs opposite, we get a symmetrical shape as shown below.
In the general case, regardless of the angles, this shape will always tile periodically:
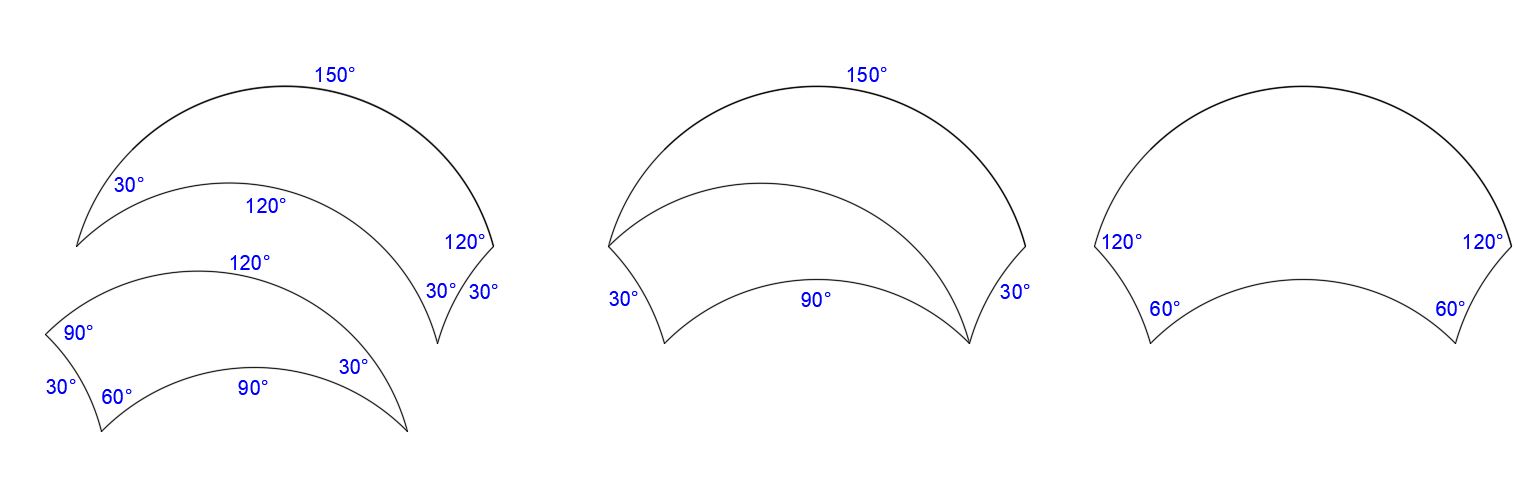
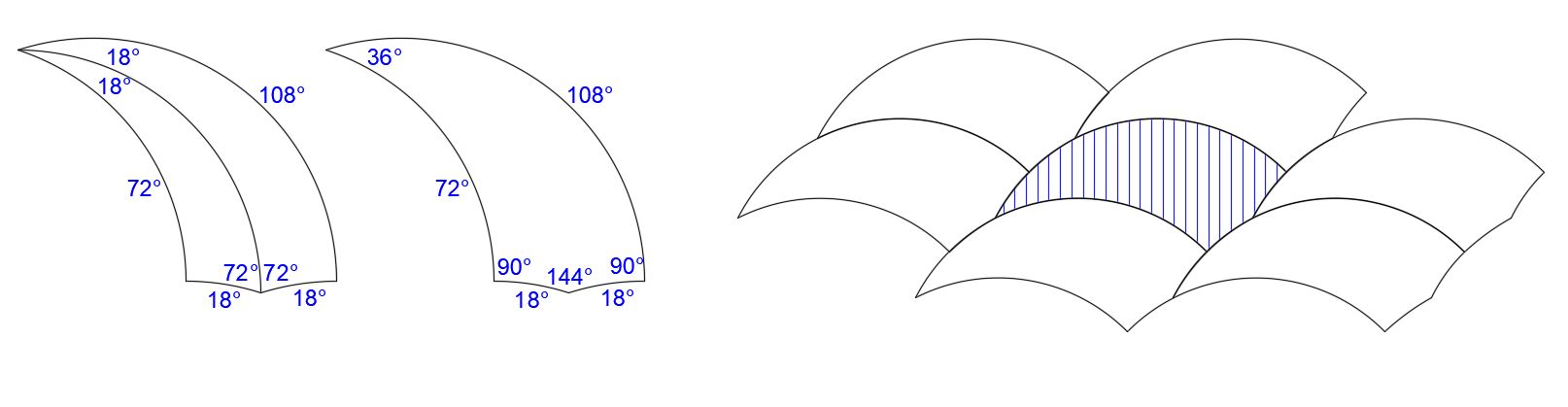
This is illustrated below, using agreeable angles. Here we have an 18°-54°-72° joined to an 18°-72°-90°. The convention here is to show arc angles on the outside of the figure, and corner angles on the inside.
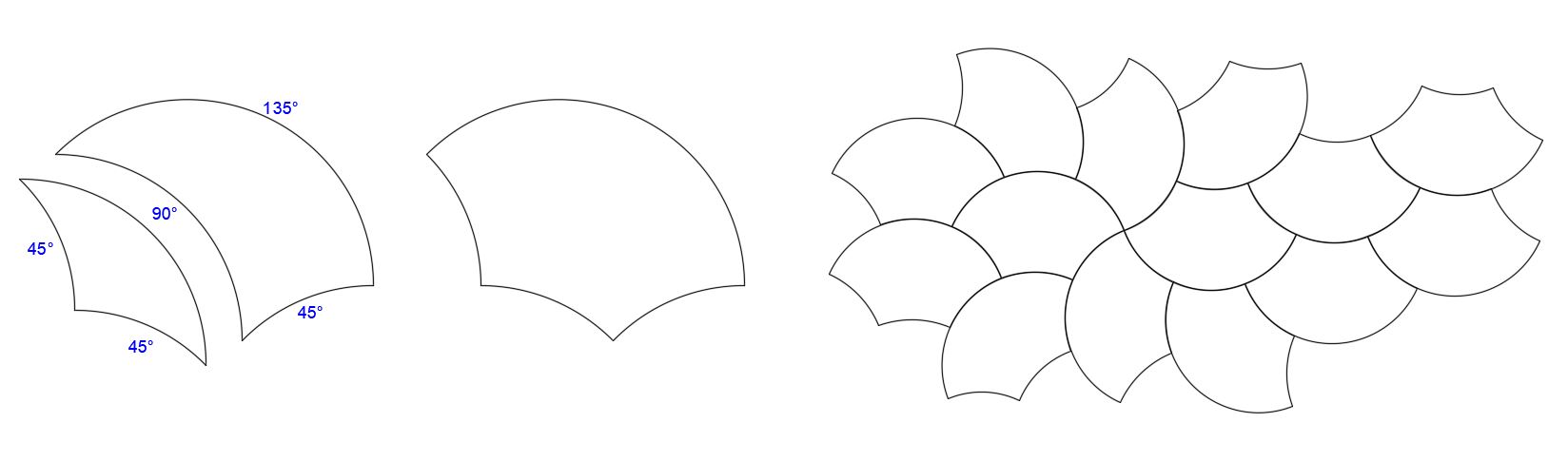
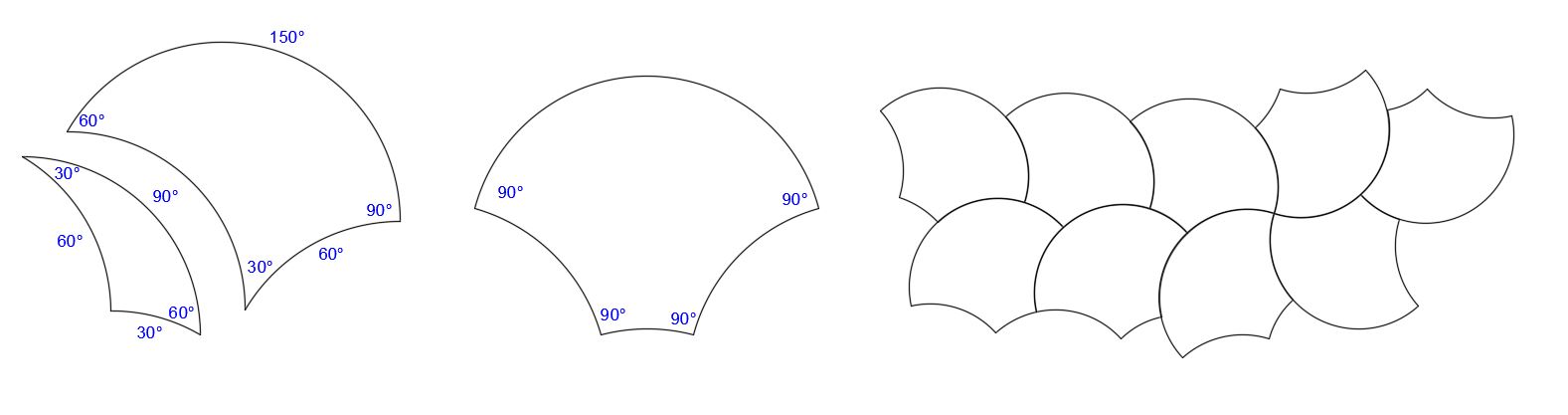
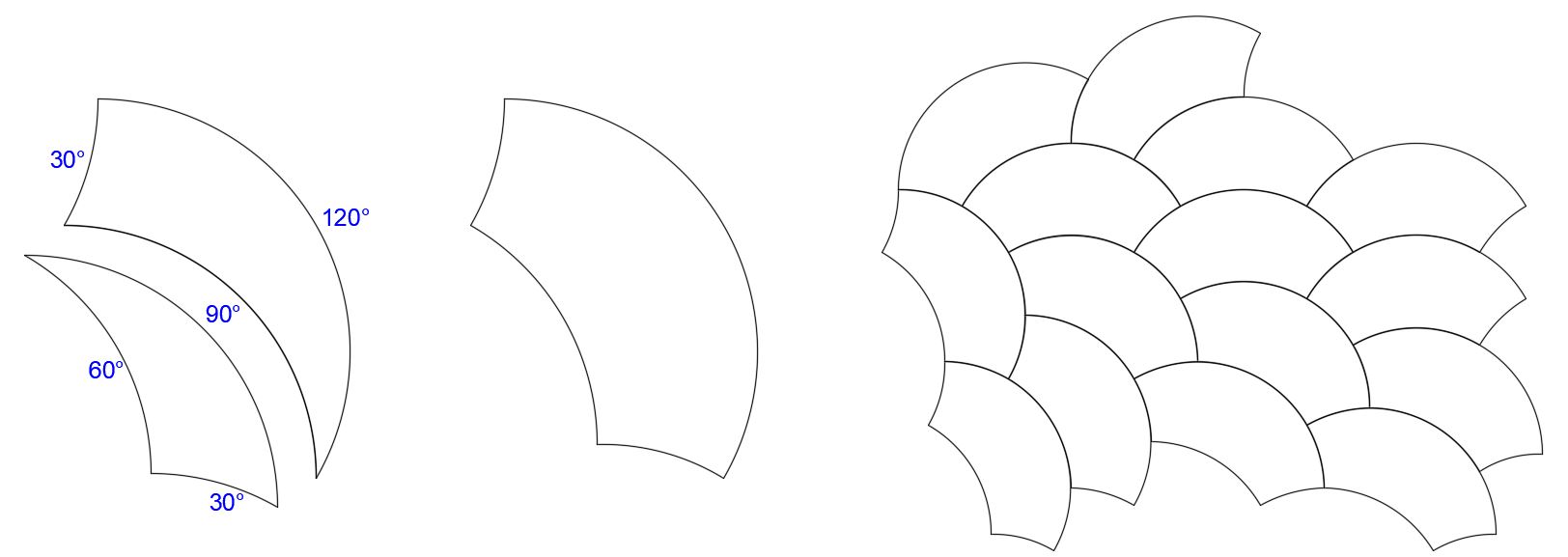
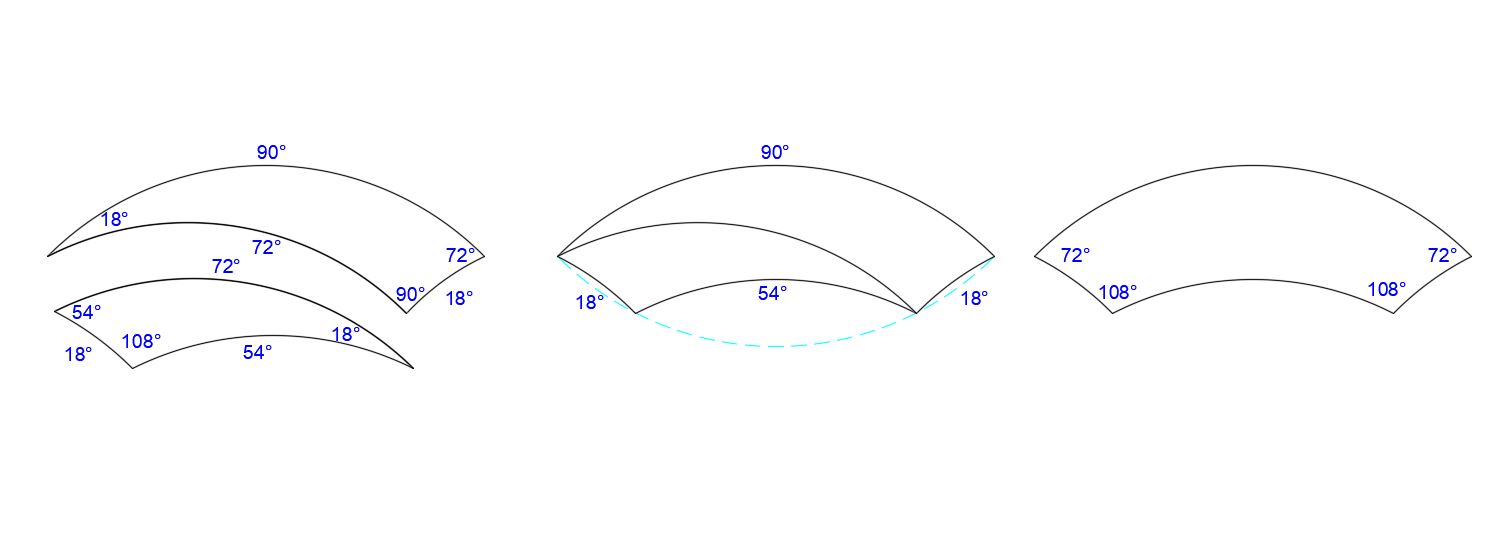 In the resulting symmetrical shape, the three smaller concave arcs sum to the large convex arc. The four corner angles sum to 360°. These arcs and angles are agreeable for tiling as shown below.
In the resulting symmetrical shape, the three smaller concave arcs sum to the large convex arc. The four corner angles sum to 360°. These arcs and angles are agreeable for tiling as shown below.
Another example is shown below, where a 30°-90°-120° is joined to a 30°-120°-150° tricurve.
In the two above examples, the combined shape has two corner angles the same as the common arc angle, with the other two corner angles the supplement of the common angle. When the common angle is 90°, all four corners of the combined shape are 90°. This makes it easy to get four-fold radial symmetry.
When an 18°-72°-90° tricurve is joined to an 18°-90°-108°, the four corners are all 90°:
With a 45°-45°-90° joined to a 45°-90°-135°, we get the three same concave 45° arcs:
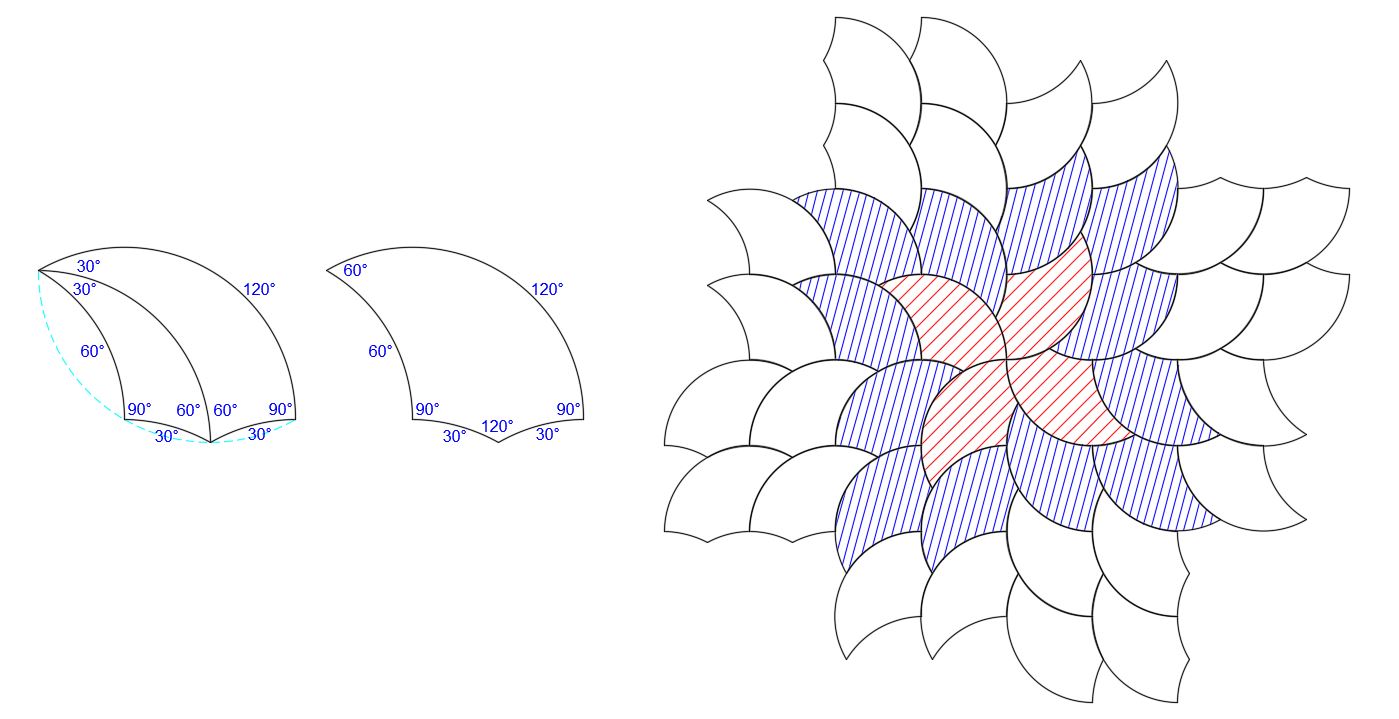
Here is a 30°-60°-90° joined to a 60°-90°-150°:
With a 30°-60°-90° joined to a 30°-90°-120°:
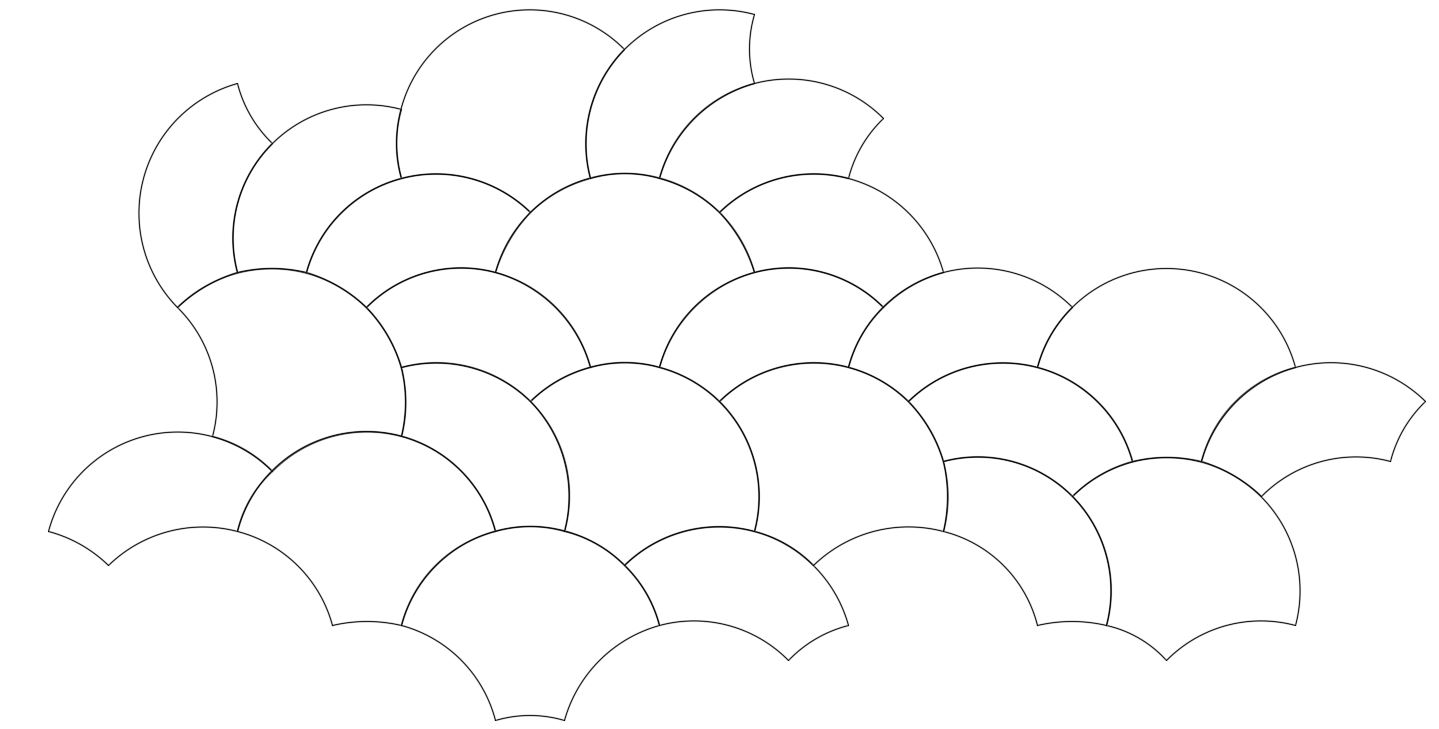
Sometimes two combined shapes can be used in tiling together, as shown below for the above two shapes:
Same Concave Arcs Together
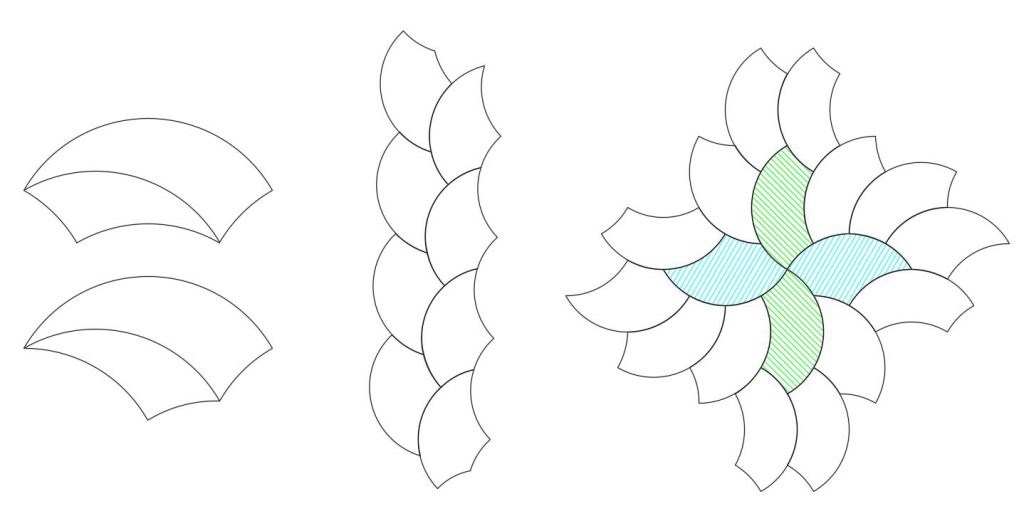
When joining a 18°-72°-90° with a 18°-90°-108° with same concave arcs adjacent, you get the shape geometry as shown below. This can tile periodically as shown, with a single tile surrounded by six of the same orientation:
This shape can also tile in a variety of ways, including this example of four-fold symmetry:
Combining a 30°-60°-90° with a 30°-90°-120°:
Author’s Note: The combined shapes formed with a shared 90° arc have many interesting properties, and these will be the subject of a planned future post. In addition, the combined shape directly above (30°-30°-60°-120°) is special: for an arc radius of one unit, the shape’s area is one square unit. Homework assignment: Why is this?
The two ways of combining tricurves produce similar shapes, which can tile together. Combining 36°-60°-90° and 30°-90°-120° gives the two shapes below, with examples of periodic tiling and two-fold symmetry.
Going Further
The examples above show a very small portion of the tricurves that can be combined, and what can be done with the combined shapes. The combined shapes shown in this post could be constructed by other means, but tricurves are good starting points, since they already are tiling-friendly and versatile. With tricurves it is much easier to get the final arc angles and corner angles you want.
Please experiment and explore these ideas, and share what you find!

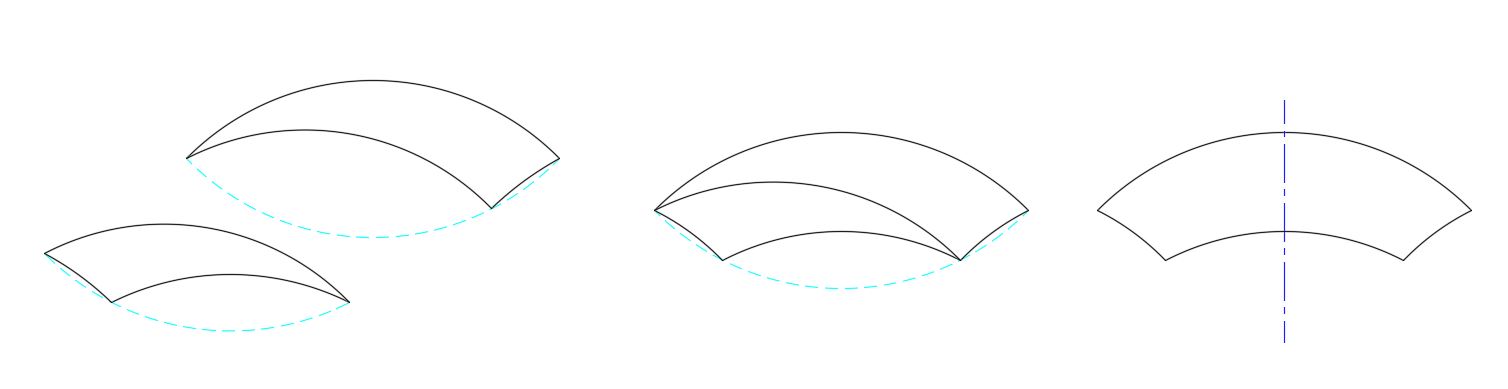
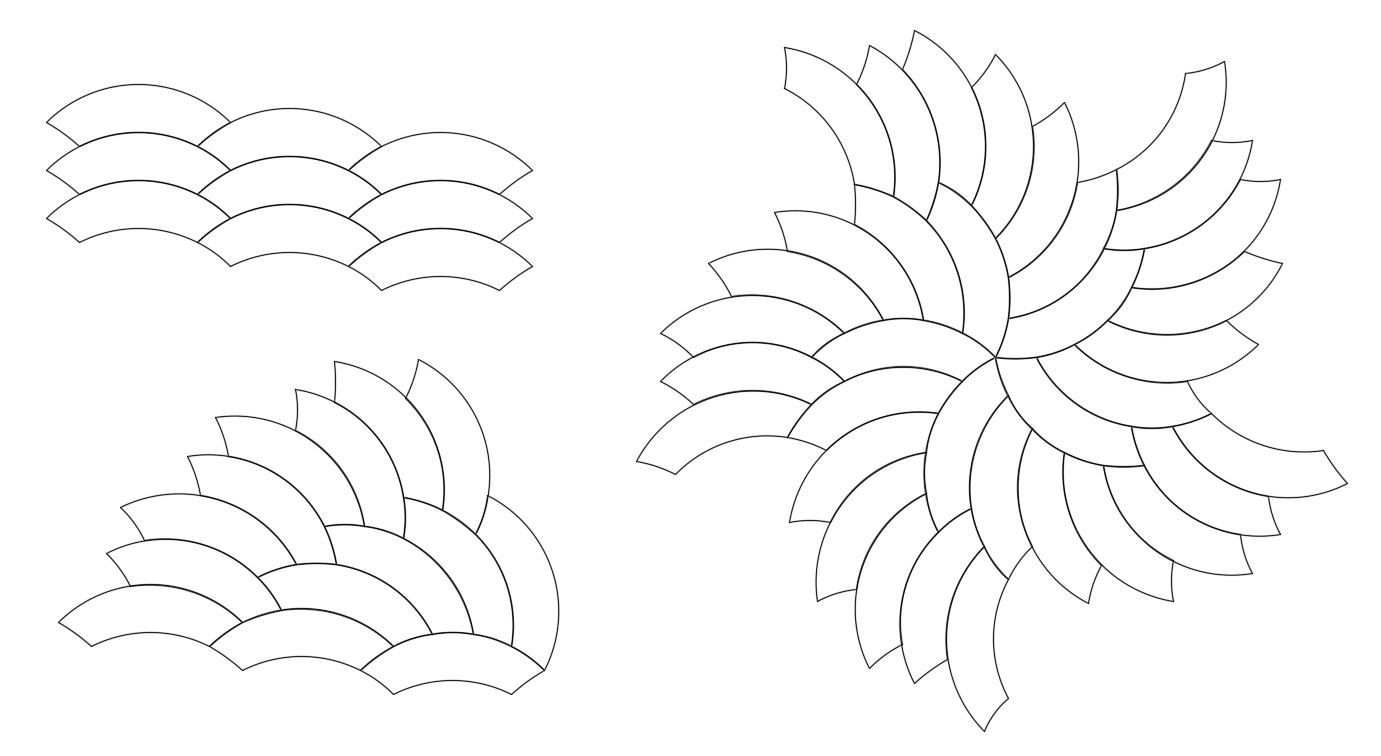
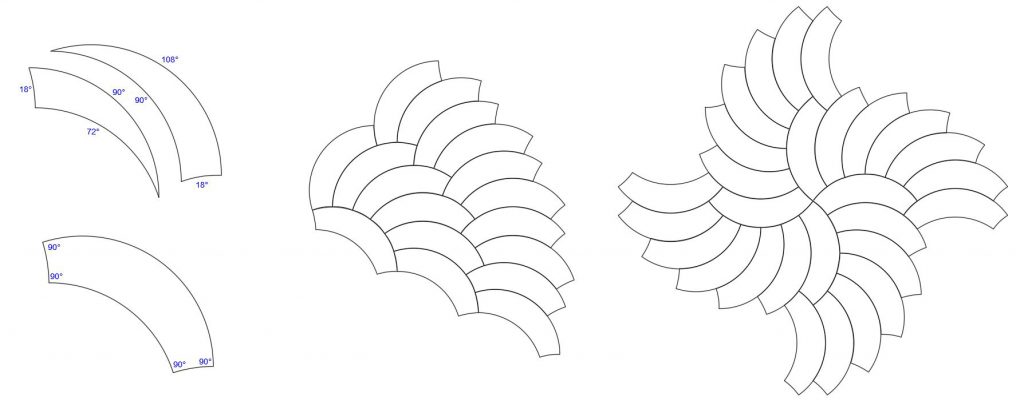
With apologies: the figure is incorrect just below the sentence: “When an 18-72-90 tricurve is joined to an 18-90-108, the four corners are all 90 degrees.” This will be corrected as soon as practical.
Never worked with curved shapes before. Interesting article.