
Surely you didn’t expect news about aperiodic tilings to appear at regular intervals? You know how it is – you wait ages for a new aperiodic monotile discovery to come along, then two come in quick succession.
In March, we covered the discovery of an aperiodic monotile. The team of authors behind that discovery have been continuing their work and this week have an even bigger announcement.
The only slightly dissatisfying aspect of the previous discovery, as you may recall, was that in order to tile the plane, the Hat (and Turtle) tile each needed roughly one in every six tiles to be mirrored. This raised the question of whether a tiling using a single aperiodic tile would be possible without reflections.
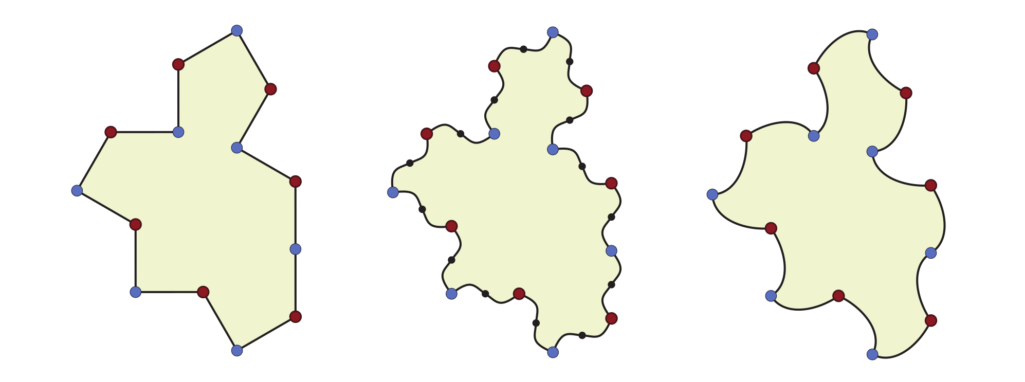
It turns out the authors had kind of already found one – a tile they referred to in their previous paper as “Tile(1,1)” was the basis for a chiral aperiodic tile – one which doesn’t need mirroring in order to fully tile.
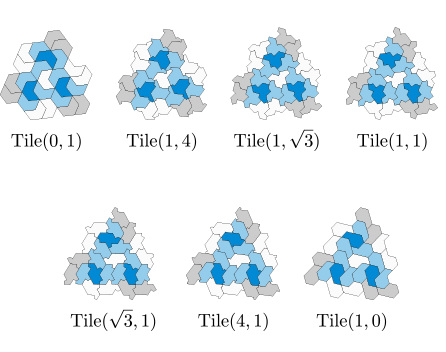
It’s actually the midpoint of the continuum of possible tile shapes that contains the hat and turtle, but had been previously considered uninteresting, since it can tile periodically if used along with its reflection. However, if you don’t use reflection, it gets more interesting.
Tile(1,1) has now been shown to be weakly chiral – meaning that if you use it without reflections, it must tile non-periodically.
This means we immediately have an infinite family of tiles with the property we’re looking for – by replacing each of the straight edges with anything that’s asymmetrical and oriented consistently, we can force the tiles to be oriented all the same way, producing an aperiodic monotile in the strong sense. (This is similar to what Edmund Harris shared in our math-off as a way to force Penrose tiles to be aperiodic.) The authors have used a simple curved line, creating a vaguely ghost-like shape they’ve christened The Spectre (because it doesn’t have a reflection, lol)
If you’d like more context and an idea of how the proof has been achieved you can check out Craig Kaplan’s webpage and his excellent Mastodon thread about it.
Hello.
Aperiodic monotiles are very interesting, but I can think of something else.
I’m thinking of creating an aperiodic monoblock in 3D. The monoblocks should be shaped in such a way that, for example, a simple shake of a container (hollow body) filled with monoblocks will cause them to quickly arrange themselves into a solid shape. I can think of a whole range of applications here, perhaps it would have such strength that by simply “pouring” the monoblocks into a vibrating mould, concrete or other building materials could be replaced. In doing so, the monoblocks could be produced by 3D printing from virtually any suitable material with suitable physical properties.
But I’m neither a mathematician nor a materials scientist, I’m just thinking.
Translated with http://www.DeepL.com/Translator (free version)
Blame your ancestry, or mathematical dogma, but some combination of ‘can we do it in 3d,’ or can we generalise for higher (or all) dimensions is virtuallly always among the first question asked.
Hello,
this was exactly my thought. I created a tile that seems to tile 3D space aperiodically.
It is very similar to the “hat” monotile in its construction.
..maybe you are not aware of this tile,
It is an aperiodic monotile for 3D with the small restriction that it allows a screw symmetry.
Hallo Tomas,
do you know the Schmitt–Conway–Danzer biprism? It is described in a Wikipedia article with the strange title “Gyrobifastigium”. Surprisingly, this 3D aperiodic monotile was much easier to be found compared to its 2D companion. One drawback of this 3D solution is the fact that it allows a certain screw symmetry (which is not periodic due to the definition) therefore it was later called “weakly aperiodic”…
Is there a way of using the Spectre itself (obviously minus one edge where this connects on to the main mass) as the “asymmetrical” and “consistently oriented” replacement for the straight edges of the original form, so as to result in a shape which retains all of the properties of the basic Spectre?
In other words, can a non-closed analogue of the Spectre’s edge be used to modify the Spectre’s edge in the iterative manner of arriving at Hilbert’s space filling lines, or fractals?
Or is the answer to that self-evidently ‘yes’, on the basis that (technically) ‘Spectre’-shaped supersets of the aperiodic tesselation of Spectres could themselves be composed of smaller Spectres?
Can i get a version without curves?
Yep, you can make one using my interactive tool.
Great little app, thank you.
Are the curved edges necessary for the non-periodicity if you are already restricted to using the tiles the same side up?
To phrase it differently, would non-curved tiles allow periodic tiling *because* it would allow tiles to be mirrored?
Paul,
It all depends whether you consider the Spectre to be one tile or two…
https://hedraweb.wordpress.com/2023/06/02/the-special-one/
Thank you for this. Tile(1, 1) with keyed edges is the most magical part of these discoveries, yet it is hardly discussed on any of the web pages that one finds by searching for aperiodic monotile. They are all about Hat, Turtle, Hat, Turtle! While the Spectre is Tile(1, 1) with curved edges, Tile(1, 1) itself needs a catchy name.
The broom
..some journalists named it “the vampire”. Maybe also “the bat” would be a nice name, but it could be easily mixed up with “the hat”…
First of all, no relation.
Second, are there guides, like are seen with some penrose tile examples, that can help one assemble the monotiles in the non-repeating manner without getting stuck. (Or, perhaps non-repeating is forced just by obvious pairing.)
Thanks.
With reference to the infinite shapes possible by varying the ratio of edge lengths…
What I’m interested in is the following:
(0,1)looks like a Chevron and requires 0 reflected pieces
(1,0) (looks like a comma?) requires 0 reflected pieces (I suspect theoretically it is 100% reflected pieces! See below)
The Hat is (√3, 1), and requires around 1/7 (?) of the tiles to be reflected;
My assumption (intuitive) is that Spectre (1,1) will require 50::50 for reflections for a periodic tesselation
So, as the dial turns from (0,1) to (1,0) I reckon there might be a ratio of reflected::unreflected that is a dependent function?
i.e. (normalising the ratios to add up to 1):
(1,0) → 0% reflected
(0.63, 0.37) → 14% reflected (Hat)
(0.5,0.5) → 50% reflected (Spectre)
(0,1) → 100% reflected
This needs a real mathematician to work it out!
I recognise a huge discontinuity in my logic here, namely: The Hat requires 1/7 reflected tiles to create an aperiodic tesselation, but I’m assuming the Spectre needs 1/2 reflected tiles to creat an *periodic* tesselation.
Hmmm…
Just as Penrose tiles tend towards the Golden Ratio (intuitively unsurprising as they are based on penta shapes) it’s interesting to wonder how these ratios might line up?
“A Spectre is now haunting Europe” (Karl Marx)