This is a guest post by Elliott Baxby, a maths undergraduate student who wants to share an appreciation of geometrical proofs.
I remember the days well when I first learnt about loci and constructions – what a wonderful thing. Granted, I love doing them now; to be able to appreciate how Euclid developed his incredible proofs on geometry.
In school, it was a slightly different story. Whilst I was meant to be constructing triangles and drawing a locus of a point, the school-supplied compasses had other ideas – slipping around unhelpfully, making them useless for the task. Understandably, I’d often put down the compass, chat with my friends, and sneakily eat crisps when the teacher wasn’t looking.
A lot has changed since then; I now have a working compass. But more than that, I have become a mathematician, mathematics teacher and all round mathematics nerd! I don’t think a day goes by where I have not been involved in some mathematical activity. My favourite on the weekend is working out how long it will be till my takeaway arrives! But I digress. Writing is a passion of mine as it allows me to share the facts and curiosities of this truly wonderful subject.
In this article I aim to share some key ideas that allowed me to develop my interest in geometry, and to appreciate the wonders hidden in plain, or rather, plane sight. Enjoy some of my favourite facts about shapes and lines, while I finish my packet of salt and vinegar crisps.
Angles in a triangle
One of the first things I learnt at school was that angles in a triangle sum to 180 degrees. But I never knew why, or saw a proof. Proof is vital in mathematics as proof allows us to confirm theories and conjectures that can help us progress our mathematical knowledge. If something is proved, then we can always assume it to be true!
I first came across this proof when I was researching different ways to teach angles in parallel lines. We will therefore be using proven facts on angles in parallel lines in this proof.
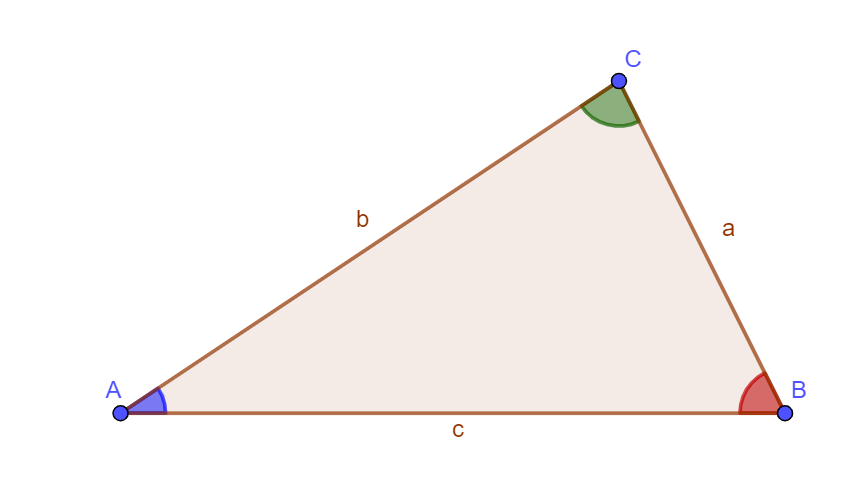
The first proof I saw of the angle sum was one using parallel lines. We start off with a triangle whose interior angles are all different (called a scalene triangle). In order to write an equation including all three angles, we first draw two lines, both parallel to the base of the triangle:
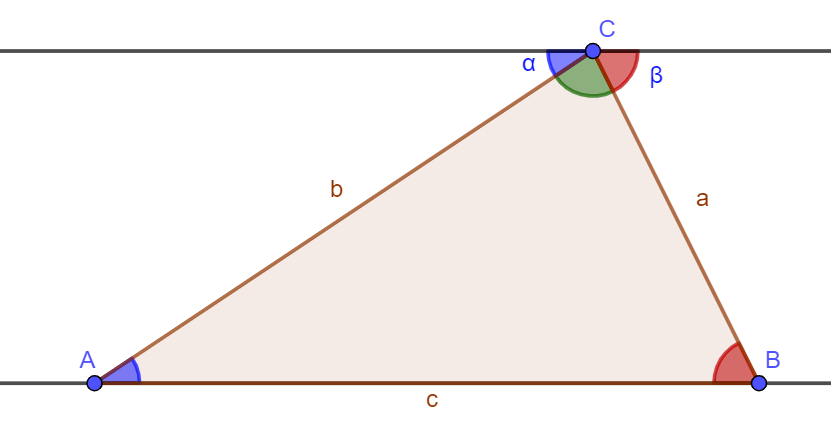
The lines \(a\) and \(b\), which are two sides of the triangle, touch both parallel lines – we say they are transversal lines. We can use some existing results about angles and parallel lines to make some deductions:
\(\angle A = \angle \alpha\) (‘alternate angles are equal’).
\(\angle B = \angle \beta \) (‘alternate angles are equal’).
\( \angle \alpha + \angle C + \angle \beta = 180^{\circ} \) (‘angles on straight lines add up to 180 degrees’)
\( \Rightarrow \angle A + \angle B + \angle C = 180^{\circ} \) QED
Here, we were able to use the fact that alternate angles are equal, as this is a proven fact. This can save time when we’re proving something that can build on existing mathematical theories.
Proof of equal sides (isosceles)
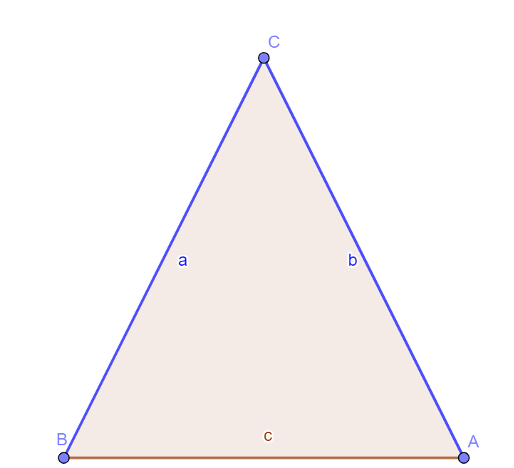
Here we have a triangle with two sides of the same length. We want to show that if this is the case, then the two base angles are equal. This proof is relatively simple, and relies on a powerful tool in geometry!
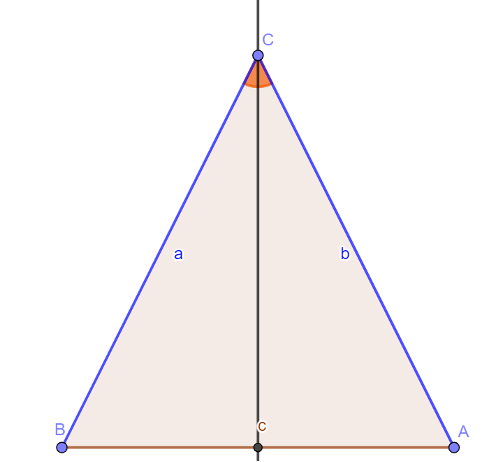
We bisect the angle at \(C\), which, in this case, will intersect at the midpoint of \(AB\) (which we denote \(c\)), as the sides \(a\) and \(b\) are the same length. It follows then, using one other existing result, that:
\( \Delta BCc \simeq \Delta ACc\) (by ‘side-angle-side’)
\( \Rightarrow \angle B = \angle A\) QED.
Congruent triangles make an appearance in a lot of geometrical proofs as they allow us to confirm certain angles or sides are equal, allowing us to draw conclusions. A related idea is that of similar triangles, which Thales used to measure the height of the Great Pyramid! But how did he do that?
Thales and the Great Pyramid
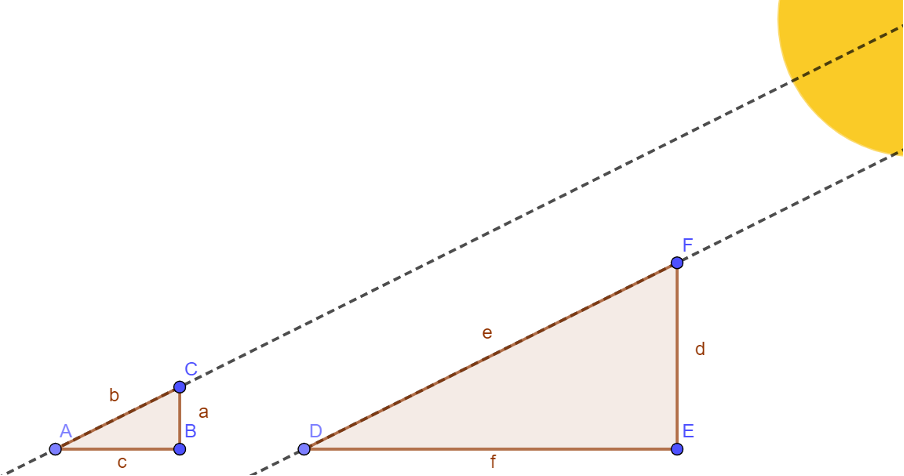
Although the Great Pyramid, and Thales, are both three-dimensional, we can model this problem by focusing on the 2D plane cutting through the pyramid, as shown in the diagram.
Thales wanted to know the height of the Great Pyramid, \(d\) and to do this is placed a vertical pole \(BC\), of height \(a\), in front of the Great Pyramid. He then measured the length of the shadow cast by the pole, \(c\) and the Great Pyramid, \(f\).
Assuming the sun’s rays are parallel, Thales drew the conclusion that the triangles formed by the tall objects and their shadows must therefore be similar, and so the height of the pole and the Great Pyramid must be in the same proportion. That is to say:
\[ \frac{d}{a}=\frac{f}{c}\]
Thales will know the lengths of \(a\), \(c\) and \(f\) so, with some rearranging, he can find the height of the Great Pyramid:
\[ d = \frac{af}{c}\]
Pythagoras
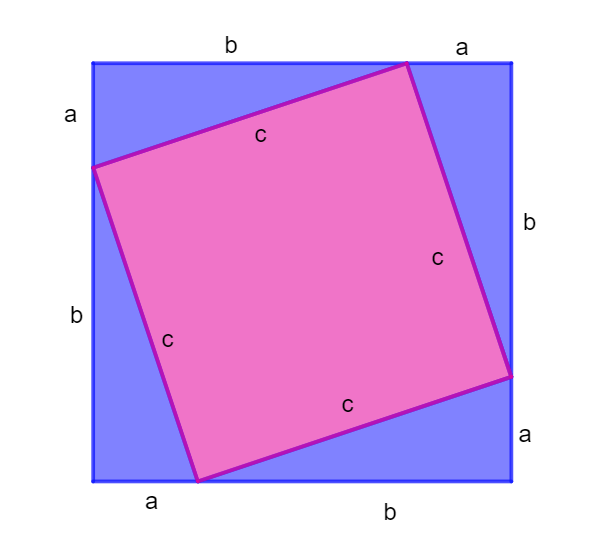
There are over 350 proofs of the Pythagorean Theorem! So many ways to prove such a simple yet powerful result. I have not seen or worked out all of them (I took a break when I got to Euclid’s proof), but the one pictured above is so far, my favourite, because it uses a lot of nice algebra.
The proof goes as follows: we start by enclosing a square with four congruent triangles, as seen above. We then want to work out the total area of the congruent triangles:
Each blue triangle has area \( \frac{1}{2}ab \), so the total area of the four blue triangles is \(2ab\).
We can also find the area of the triangles in another way. Because the four triangles are congruent, the sides form a larger square of length \( (a+b) \), and the area of the pink square will be \(c^2\). From this, we can work out the total area of the triangles a different way:
Total area of blue triangles \(= (a+b)^2 – c^2\)
We now have two ways to write the area of the blue triangles, so we can equate these two expressions:
\[ (a+b)^2 – c^2 = 2ab\]
\[ a^2 + 2ab + b^2 – c^2 = 2ab \]
\[ a^2 + b^2 – c^2 = 0 \qquad \textrm{(Subtracted }2ab\textrm{ from both sides)}\]
\[ a^2 + b^2 = c^2 \qquad \textrm{(Added }c^2\textrm{ to both sides)}\]
QED.
The proof is complete!
Geometry and Algebra
Mathematics started to become a passion for me when I first learned about expanding quadratics – it was the first topic I revised when preparing for my GCSEs. I remember spending ages on this topic, because I kept making mistakes when multiplying negatives and positives, but I kept persevering. I even rushed my tea to go and continue to expand brackets! But don’t worry, I took some crisps with me.
The obsession stemmed from the fact that it was extremely fun! I knew I had an end goal and I had to work towards it – double checking to make sure each step I took was correct. Algebra became one of my favourite pastimes, and increased my love for mathematics. So, when I heard there was a link between expanding brackets and geometry, I was excited to learn more.
If we expanded \((a+b)^2\), we would get \(a^2 +2ab + b^2\). But why? It may not initially seem that obvious. We can prove this using the distributive property – but that’s not what this post is about… so let’s use geometry!
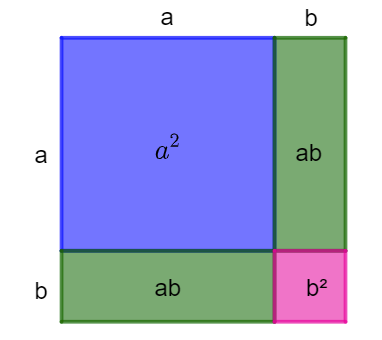
We start by drawing a square of side length \((a+b)\). We then divide the square up into different sections: we can make a square of length \(a\)(blue square), then cut out 2 congruent rectangles with dimensions \(a\) by \(b\) (green rectangles). We are then left with a pink square that has side length \(b\).
If we work out the areas of each of these 4 shapes, the sum of these areas will equal the total area of the initial square.
The sum of the areas:
\[ \textcolor{blue}{a^2 \textrm{ (blue) } } + \textcolor{green}{ab \textrm{ (green)}} + \textcolor{green}{ab \textrm{ (green)}} + \textcolor{magenta}{ b^2 \textrm{ (pink) }} \]
Therefore, this will be equal to the area of the initial square, which measures \((a+b)\) on each side:
\[ (a+b)^2 = a^2 + 2ab + b^2 \]
I do quite like this result as it links to my first ever real enjoyment of learning mathematics!
Puzzle
I would like to end with a little puzzle for you. Can you work out the area of the green section, in this triangle with circle arcs centred at each corner?

The solution is below.
Geometry Rules
I am now reaching the end of my crisps and so, like at school, it is time to call it a day. Geometry is fascinating. There is no denying that. The theorems, proofs, applications are truly something to behold, and we can see the connections between solving equations and drawing shapes! But this article barely scratches the surface of the wonder that is geometry so, when I get a new packet of crisps, I will be sure to share more of the fascinations geometry has to offer.
Area Puzzle solution
The triangle is equilateral, since all the sides are the same length. Using Pythagoras to work out the height, \(h\), of the triangle:
\[h^2 + 4^2 = 8^2\]
\[h^2 + 16 = 64\]
\[h^2 = 48 \]
\[ h = 6.928\ (4 s.f.)\]
Area of triangle:
\[ \frac{1}{2}\cdot 8 \cdot 6.928 = 27.71\ (4 s.f.)\]
Area of sectors:
\[ \frac{60^{\circ}}{360^{\circ}}\cdot \pi(4^2)\]
\[ \frac{16\pi}{6} = \frac{8\pi}{3}\]
As there are 3 congruent sectors, total area of sectors:
\[ 3 \cdot \big( \frac{8\pi}{3} \big) = 8\pi\]
Therefore, area of the green section:
\[ A = 27.71 – 8\pi\]
\[A = 2.587\ (4 s.f.)\]
Loved it, was such a good read. The proofs were simple enough for simpletons like me to understand. I liked the anecdote at the start of the paper too