It’s math-off time!
Here’s the first match in this year’s Big Internet Math-Off. Today, we’re pitting Katie Steckles against Benjamin Dickman.
Take a look at both pitches, vote for the bit of maths that made you do the loudest “Aha!”, and if you know any more cool facts about either of the topics presented here, please write a comment below!
Katie Steckles – Prime Chunks of π
I’m always on the lookout for interesting maths, and one place I often find some of the most interesting stuff is in the crossovers between different mathematical ideas. What happens when you look at the intersection of topological shapes and colouring problems, or the parts where functions meet fractals, or the crossover between flexagons and the fold and cut theorem? (I’m not saying any of these are potential ideas for my entries in future rounds of the Math Off, but I’m also not not not not saying that.)
One of my favourite mathematical crossovers comes between two numerical classics of the genre: prime numbers, and π. Everyone’s \(\frac{\tau}{\pi}\)th favourite circle constant, meeting the indivisible building blocks of the integers. What could possibly go wrong?
We all know that the digits of π go on forever, and never repeat. This makes them a useful source if you ever want a string of seemingly random digits, since they keep going and there’s not a discernible pattern in them. But what if we look for a pattern in them? And in particular, if we look for prime numbers?
For example, the first digit (3) is a prime. Success! But for the sake of argument, let’s keep going. The next digit (1) is, assuming we’re doing it right, not a prime number.
But if we look a little further, and include the following digit as well, we get the number 14, which is… also not a prime. But 141, which we make by extending a little further, is… also not a prime number.
With a little patience, we’ll find (having been disappointed once more by 1415, which is shockingly divisible by 5), that we can go as far as 14159, which is gloriously prime. It’s also immediately followed by 2 – straight in the bucket of primes.
This can continue – the disappointment of 6 and 65 are outweighed by the beauty of the prime that is 653. It’s followed by 5, one of the classic small primes, then (not 8 but) 89, then 7.
9 isn’t prime (as much as my subconscious brain wants to include it whenever I give a list of primes), nor is 93, or 932 – but 9323 is, giving us another wonderful entry on our list.
And you might imagine we can carry on this way, theoretically forever – chunking off prime pieces of π and serving them up with ice cream. But while the digits of π do theoretically provide an infinite string of primes using this method, not all of them are quite so easy to swallow.
At this point in the decimal expansion of π, we find an unhelpful succession of frustratingly even digits: 8, 4, 6, 2, 6, 4 – none of which are of any use to us at all in making another prime. In fact, the next chunk of digits we can section off into a prime number is actually
846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432664821339360726024914127372458700660631558817488152092096282925409171536436789259036001133053054882046652138414695194151160943305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912983367336244065664308602139494639522473719070217986094370277053921717629317675238467481846766940513200056812714526356082778577134275778960917363717872146844090122495343014654958537105079227968925892354201995611212902196086403441815981362977477130996051870721134999999837297804995105973173281609631859502445945534690830264252230825334468503526193118817101000313783875288658753320838142061717766914730359825349042875546873115956286388235378759375195778185778053217122680661300192787661119590921642019893809525720106548586327886593615338182796823030195203530185296899577362259941389124972177528347913151557485724245415069595082953311686172785588907509838175463746493931925506040092770167113900984882401285836160356370766010471018194295559619894676783744944825537977472684710404753464620804668425906949129331367702898915210475216205696602405803815019351125338243003558764024749647326391419927260426992279678235478163600934172164121992458631503028618297455570674983850549458858692699569092721079750930295532116534498720275596023648066549911988183479775356636980742654252786255181841757467289097777279380008164706001614524919217321721477235014144197356854816136115735255213347574184946843852332390739414333454776241686251898356948556209921922218427255025425688767179049460165346680498862723279178608578438382796797668145410095388378636095068006422512520511739298489608412848862694560424196528502221066118630674427862203919494504712371378696095636437191728746776465757396241389086583264599581339047802759009946576407895126946839835259570982582262052248940772671947826848260147699090264013639443745530506820349625245174939965143142980919065925093722169646151570985838741059788595977297549893016175392846813826868386894277415599185592524595395943104997252468084598727364469584865383673622262609912460805124388439045124413654976278079771569143599770012961608944169486855584840635342207222582848864815845602850601684273945226746767889525213852254995466672782398645659611635488623057745649803559363456817432411251507606947945109659609402522887971089314566913686722874894056010150330861792868092087476091782493858900971490967598526136554978189312978482168299894872265880485756401427047755513237964145152374623436454285844479526586782105114135473573952311342716610213596953623144295248493718711014576540359027993440374200731057853906219838744780847848968332144571386875194350643021845319104848100537061468067491927819119793995206141966342875444064374512371819217999839101591956181467514269123974894090718649423196156794520809514655022523160388193014209376213785595663893778708303906979207
Yes, that’s a prime number 3057 digits long. After teasing us with manageable 2-, 3- and 4-digit beauties, and even some delicate single-digit primes, the decimals of π have dumped in our lap a heap of digits so vast it’s almost boring.
This seems like an incredible coincidence. What would possibly possess whichever number devil wrote this number to make it have such a strange distribution of prime lengths? But when I thought about this a little longer, I gradually realised what was going on here.
While the prime numbers, much like the digits of π, are mysterious and unpredictable, there are some patterns they’re known to follow. The Prime Number Theorem tells us that for a given value N, the number of primes less than N can be relatively well predicted.
The prime counting function \(\pi(N) = \frac{N}{\ln(N)}\) tells me that there are roughly 21 primes less than 100 (in fact there are 25), 144 primes below 1000 (actually there’s 168) and 1086 primes below 10,000. But these ranges are getting bigger much quicker than the number of primes is: the prime numbers get further apart as the numbers get larger, and the density is decreasing.
This also means that given a particular number of digits, the probability that any given random string of digits of that length is a prime will get smaller very quickly as the numbers of digits gets larger; roughly 8.6% of 5-digit numbers are prime, and only 7.2% of 6-digit numbers.
So if we’re looking for primes in a specific string of digits, we’re relying heavily on these probabilities to line up if we want to keep finding primes – and once we get into 6 or 7 digits, that probability gets pretty low. All we’d need to trip us up is a successive string of, say, digits divisible by 2 or 5, none of which can occur at the end of a prime number written in base 10, and we’d… oh.
So that chunk of even digits is much more or a problem than it initially seems – by the time we get to numbers that start 846264, the primes are so spaced out that none of the possible digits placed in that next spot would give a prime. And of the numbers starting 8462643, only one of them – 84626431 – is prime (but sadly π just gives us another 3). Once we reach this length of string, the probability of hitting another prime is so small, it’s easy to see how it takes a very long time before we get to the next one.
It doesn’t get much better after that either – the next digits of π are 73, then 467 (two perfectly manageable primes), but then we dive off into a 14650-digit monster. (for reference, A047777 in OEIS is the primes, and A121267 gives the corresponding lengths).
Another nice consequence of this is that it’s not a phenomenon unique to π – other infinite non-repeating decimal expansions also suffer from gigantic prime chunks. e starts with a 2, then a 7, then the next prime is 649 digits long. The square root of 2, with its unhelpful ‘14142’ opener, takes 55 digits before we even get to the end of our first prime. But even though the maths tells us this kind of thing is likely, it still somehow feels a little unexpected.
So the next time you’re looking for an interesting fact about π to share, try chopping it up into prime numbers and watch people’s faces when you tell them what happens.

 Katie Steckles is a mathematician based in Manchester, who gives talks and workshops and writes about mathematics. She finished her PhD in 2011, and since then has talked about maths at universities, schools events, festivals, on BBC radio and TV, in books and on the internet. You can find her on Mathstodon, Instagram, and as part of The Finite Group (and here on The Aperiodical).
Katie Steckles is a mathematician based in Manchester, who gives talks and workshops and writes about mathematics. She finished her PhD in 2011, and since then has talked about maths at universities, schools events, festivals, on BBC radio and TV, in books and on the internet. You can find her on Mathstodon, Instagram, and as part of The Finite Group (and here on The Aperiodical).
Benjamin Dickman – Sharing is Caring
I’m hopeful that The Big Internet Math-Off will bring mathematical joys – and perhaps even surprises! – to its readers. Thinking back, here are a couple of mathematical tidbits that I enjoyed and/or surprised me back when I was young and still had light behind my eyes:
- I always enjoyed sequences and series, and I recall learning that the sum \(\sum_{n\geq 1} 1/n^p\) converges when \(p \gt 1\). Seeing that it diverged for \(p = 1\) was enjoyable, but not knowing what it converged to for \(p \gt 1\) was an early frustration of mine. Pleasantly, I learned that at least one value is well known: \(\sum_{n\geq 1} 1/n^2 = \pi^2/6\).
- Mathematicians finish their proofs in different ways: after \(n\) too many jokes about “Q.E.D.” standing for “Quite Easily Done,” I have come to enjoy the various boxes that are often referred to as tombstones. A reminder not only that mathematics is alive, but also that every time you use a result or its proof, you are essentially invoking a zombie.
For today’s mathematical vivacity let us consider the following problem:
Randomly pick two positive integers; what is the probability that their only shared factor is 1?
Now, you cannot really pick two elements at random from the positive integers; so, let us be a bit more precise and say… pick two positive integers in [1, really big]. The mathematical term for their largest shared factor is the greatest common divisor, which is often abbreviated as gcd, and we say that positive integers whose only shared factor is 1 are relatively prime. This means that the sharing that we are caring about can be rephrased as:
What is the probability that two “randomly” chosen positive integers are relatively prime?
We will solve this problem in mere moments, but first: What does your intuition tell you? If you want to test your intuition, you could try typing gcd(a,b) into WolframAlpha where each of a and b is formed by mashing a number pad. I tried this just now and, indeed, they are relatively prime. Give it a shot!
My intuition unfolds as follows: With a probability problem, the answer is probably 0 or 1; it could be ½ to be tricky; and, in cases where the problem is unfamiliar, it is probably 1/e or something related. If you want to gather more data from WolframAlpha, go for it; I ended up using GPT to simulate this 100,000 times for positive integers chosen in the range [1, 1050]. The simulation found the proportion with a gcd of 1 to be 0.60813.
My intuition now suggests that this is converging to \(1-1/e = 0.6321\ldots\) I’ve seen enough problems to make that guess with confidence of, idk, about \(1/e\); the next step could be to verify it, but that is difficult to do for a conjecture that is flat out wrong.
Okay: Let’s investigate the problem and find the correct answer! Imagine the first quadrant in the xy-plane and make a dot at \((a,b)\) when \(\gcd(a,b) = 1\). We will focus only on points with coordinates that are both positive integers, which transforms our problem into: Zooming further and further out, what proportion of the total coordinates have dots?
Here is a graph of the dots as \(a\) and \(b\) range from 1 to 1000:
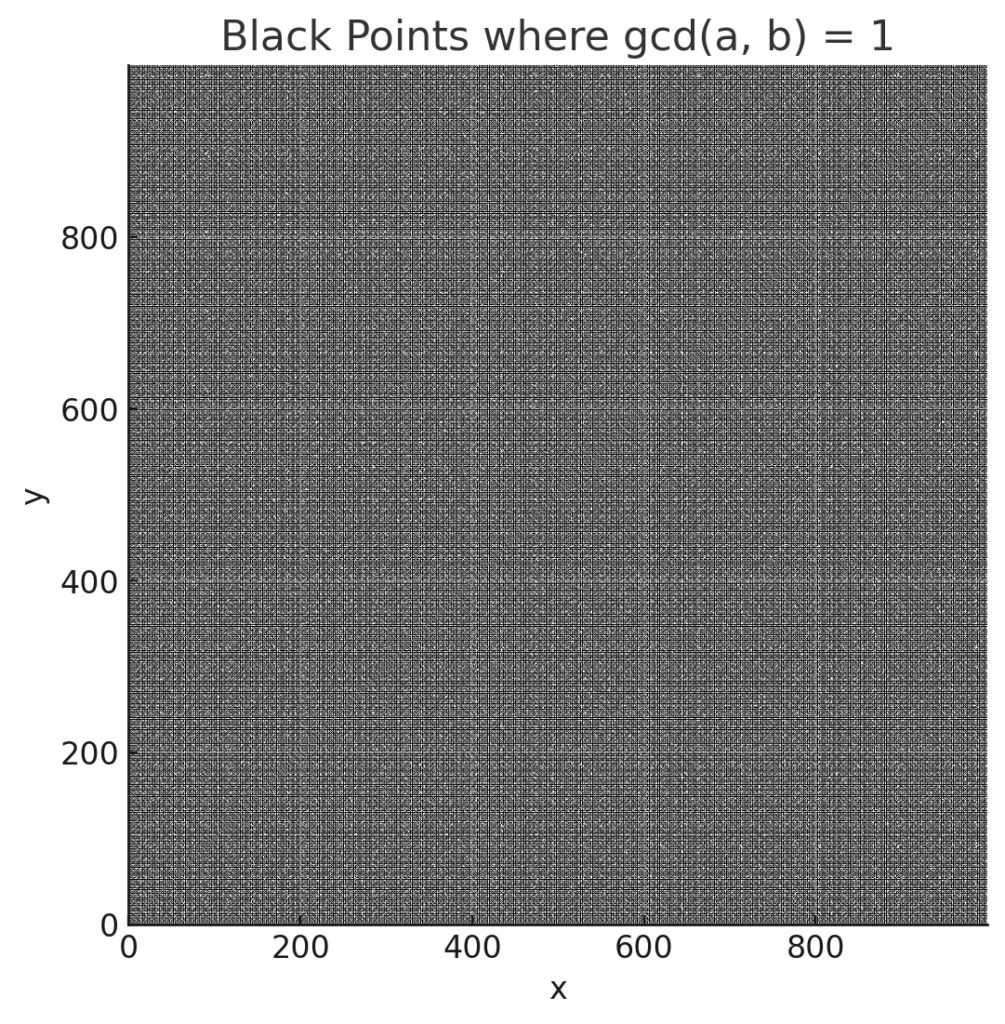
Visualization is a great tool for making sense of mathematics problems. And. I do not find this particular graph to be especially helpful – at least for finding the exact answer. The graph does suggest that the ratio probably (?) is not going to zero. But who knows!
Let’s zoom in a bit and consider integers chosen in [1, 100]:
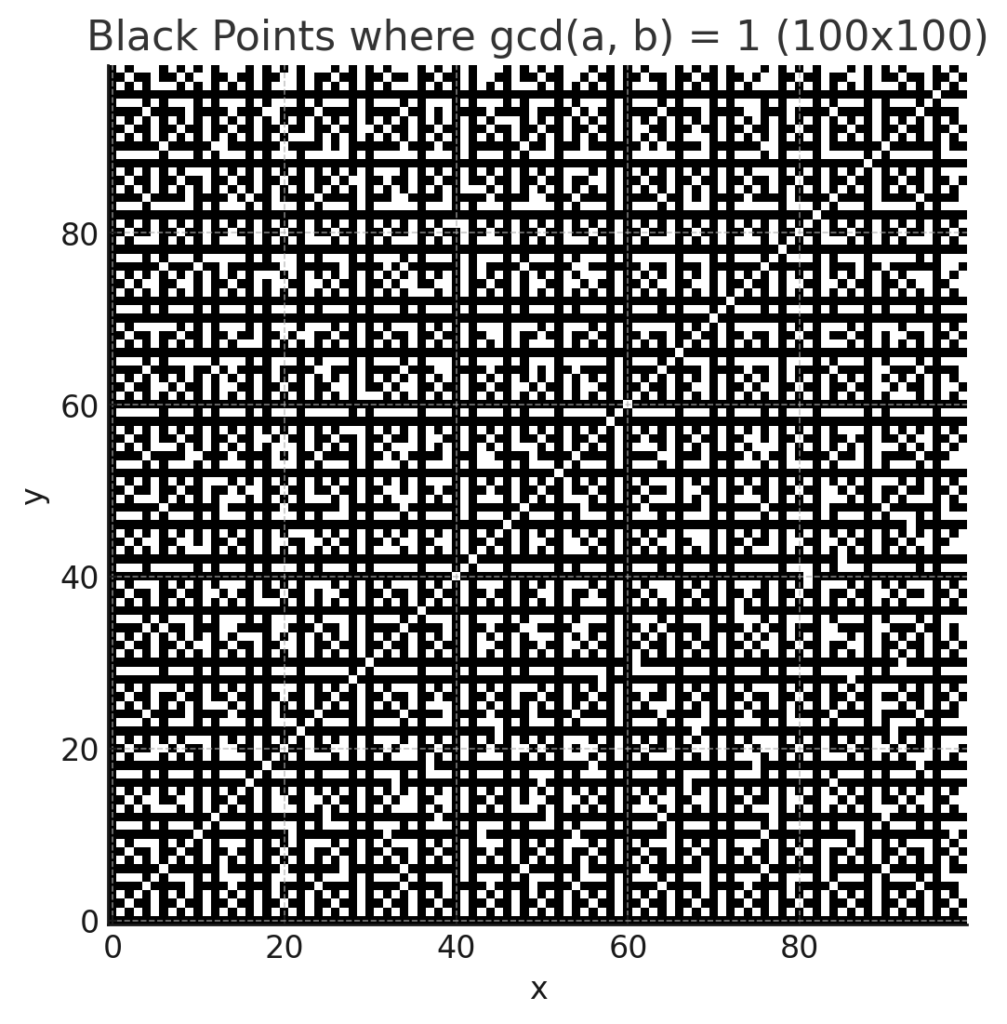
(A sensemaking checkpoint: Why are there no black dots along the main diagonal? And why are there so few along the horizontal and vertical lines emanating from 30?)
Rather than staring at the black dots in search of an epiphany, let us consider what is happening for the white dots. We know that they indicate a gcd that is greater than 1; so, let’s try putting dots at \((a,b)\) when \(\gcd(a,b) = 2\); then try it for \(\gcd(a,b) = 3\). Maybe we’ll try \(\gcd(a,b) = 4\) later.
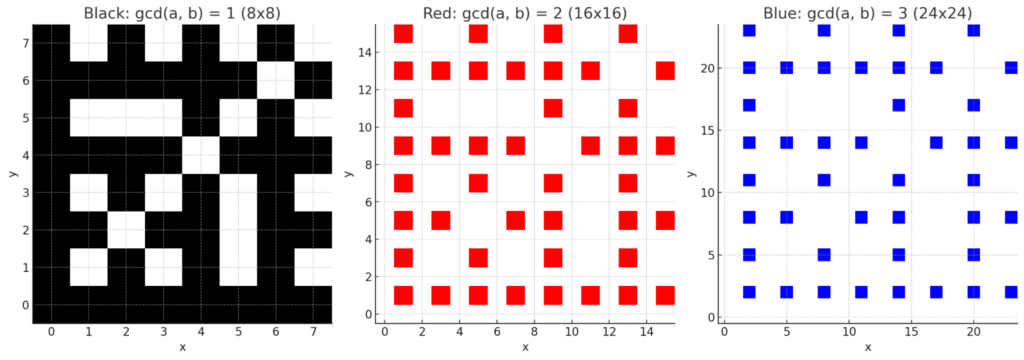
Now, the astute reader (either the one who is already astute, or the one who will momentarily become astute) will notice that the three graphs above have different ranges from which the integers were chosen. The idea is as follows: Consider points \((a,b)\) such that \(\gcd(a,b) = 1\). We can now consider \((2a,2b)\) to match them up with points that have a gcd of 2. Similarly, we could triple them and consider \((3a,3b)\) to match them up with points that have a gcd of 3.
When we look at Table 3, we see that the picture for gcd=1 among [1,8] looks rather like gcd=2 among [1,2×8], and both look rather like the image for gcd=3 among [1,3×8]. (Look at the dots and blank spaces!) If we pursued this further, our next graph would investigate gcd=4 among [1,4×8]. Perhaps you are now prepared to predict what it will look like:
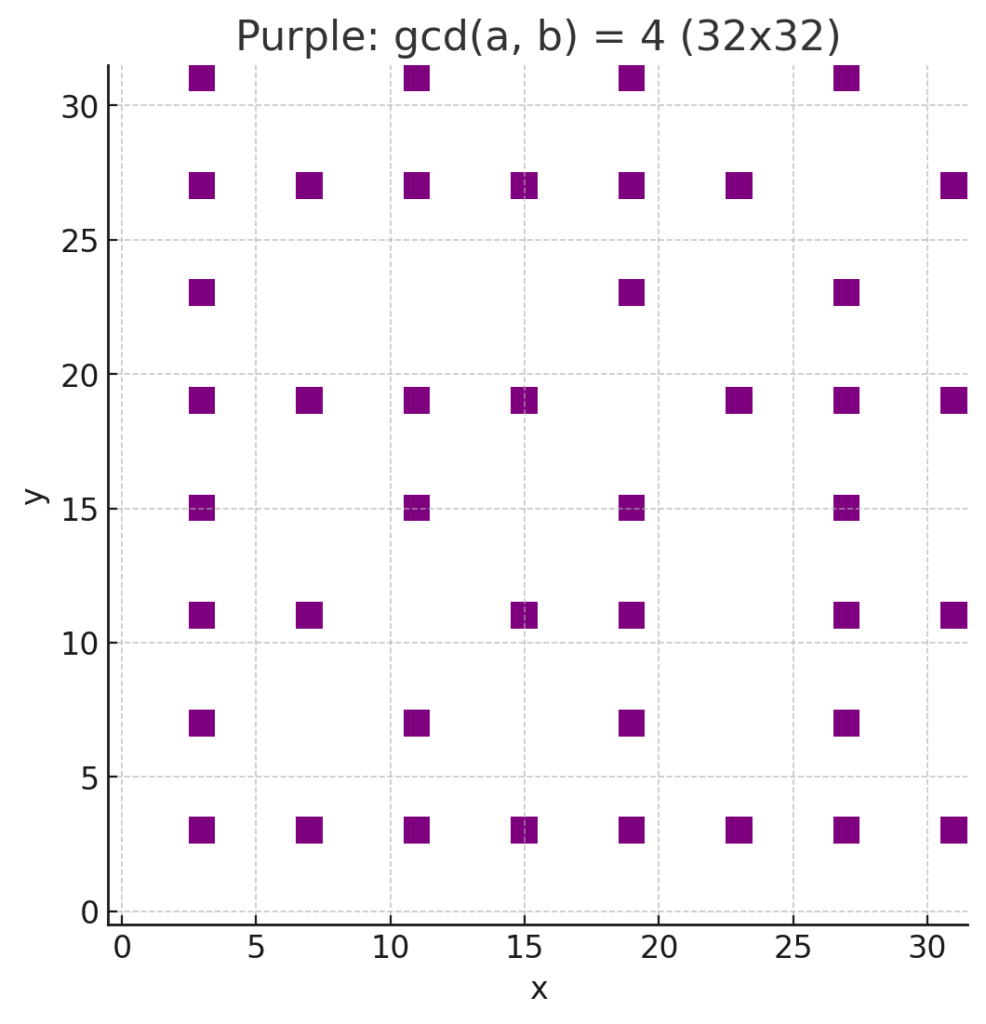
At this point, we are nearing the finish line. The remainder of the argument, modulo a bit of hand waving, goes as follows:
Color the points with gcd=1 in a first color; color those with gcd=2 in a second color, and observe that the latter match with the former using a transformation of \((a,b) \to (2a,2b)\), which means that, in some sense, they appear only 1/4 as often. Similarly, we color those with gcd=3 in a third color and, due to the matching of \((a,b) \to (3a,3b)\), they appear only 1/9 as often as the first batch of points. Continuing in this way for all positive integers, let us denote by p the proportion that we are interested in, namely, those with gcd=1. Then, the proportion with gcd=2 can be expressed as \(p/4\), the proportion with gcd=3 as \(p/9\), and so forth, from which we can sum them all up to find:
\[ p + \frac{p}{4} + \frac{p}{9} + \frac{p}{16} + \ldots + \frac{p}{n^2} + \ldots \]
How can we interpret this series? Well, the first term is the probability we are interested in, i.e., that two randomly selected positive integers have gcd=1; the second term is the probability that they have gcd=2; etc. Continuing on (and on and on) we can view this infinite series as accounting for all possible gcd’s; since any pair of numbers must have some gcd, the series at hand covers all possible scenarios without overlap. In particular, it sums to 1:
\[ p + \frac{p}{4} + \frac{p}{9} + \frac{p}{16} + \ldots + \frac{p}{n^2} + \ldots = 1 \]
Understanding this step (or, at the least, making peace with it) prepares us to solve for p: We factor it out from the left hand side to find:
\[ p\left(\frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \ldots\right) = p\left(\sum_{n \geq 1} \frac{1}{n^2} \right) = p\left(\frac{\pi^2}{6}\right) = 1 \]
where we used the first item at the beginning of this post to rewrite that parenthetical infinite series as \(\pi^2/6\). This leads us to an answer of \(p=6/\pi^2 = 0.6079\ldots\), which fits rather nicely with our earlier simulation! And that is the answer: \(6/\pi^2\) (just like my intuition suggested… 👀)
The reader is encouraged to press forward with other explorations; you might consider the probability that among three “randomly” chosen positive integers the probability that their gcd (the greatest common divisor that goes evenly into all three integers) is 1. A similar argument, perhaps even graphed with different colored points in a cube, leads to an analogous answer with our initial series changed to have an exponent of three: \(1/\left(\sum_{n \geq 1} \frac{1}{n^3}\right)\).
You may wonder whether this last number’s denominator has a snazzy formula like \(\pi^2/6\). The answer is… unknown! In fact, not much is known about this number. It’s called Apéry’s Constant and named after Roger Apéry – a mathematician who proved it’s irrational. In fact, our friend Roger was so pleased with his proof that it’s an irrational number that he memorialized it as a Q.E.D. on his own life: a rather fitting way to close out our write-up:
Notes
1. This write-up is based on the wonderfully assembled PCMI (Park City Mathematics Institute) Summer 2023 materials.
2. Thank you to Jay Cummings for bringing this gravestone to my attention in a twxxt.
3. You can find a bit more about Apéry’s Constant in the Aperiodical in an appropriately named post called Apéryodical. (The assertion proved here is stated in that post without proof!)
4. If you want to try your hand at a further problem, we closed with a “proof” concerning the case of three positive integers that share no common divisor other than 1. A variation on this question would be to ask for the probability that, among three randomly selected positive integers, any two of the three have gcd=1; in other words, what is the probability that they are pairwise relatively prime? What does your intuition tell you?
5. Generalize the problem in Note 4 to the case of k randomly selected positive integers being pairwise relatively prime. What does my intuition tell me?
6. A different proof approach uses something called Möbius inversion. Write out your own explanation using this alternative approach. I don’t really know what Möbius inversion is, so I will appreciate it if you can make it understandable to me!
 Benjamin Dickman is a mathematics teacher at a girls’ day school in New York City and a two-time Fulbrighter. His doctoral dissertation was on creativity and problem posing with the times table. He created the word game FiddleBrix! You can find him on X and Bluesky.
Benjamin Dickman is a mathematics teacher at a girls’ day school in New York City and a two-time Fulbrighter. His doctoral dissertation was on creativity and problem posing with the times table. He created the word game FiddleBrix! You can find him on X and Bluesky.
So, which bit of maths has tickled your fancy the most? Vote now!
Match 1: Katie Steckles vs Benjamin Dickman
- Benjamin with gcds and 6/π²
- (61%, 126 Votes)
- Katie with prime chunks of π
- (39%, 82 Votes)
Total Voters: 208
This poll is closed.
The poll closes at 08:00 BST tomorrow. Whoever wins the most votes will get the chance to tell us about more fun maths in the quarter-final.
Come back tomorrow for our second match in round 1, pitting Angela Tabiri against Max Hughes, or check out the announcement post for your follow-along wall chart!
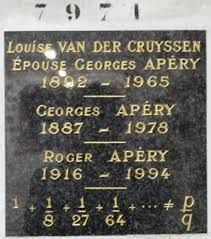
This is going to be fun!
From what I know about reader polls and long articles, the first article is going to have a big advantage over the second one. Have you considered presenting them equally somehow? Perhaps by randomising their order on the page, or by having parallel links?
Good to know; I will [try to] keep the length in mind for round two!
hard choice…