Welcome to the 241st Carnival of Mathematics, hosted here at the home of the Carnival, The Aperiodical. The Aperiodical is a shared blog written and curated by Katie Steckles (me), Christian Lawson-Perfect and Peter Rowlett, where we share interesting maths news and content, aimed at people who already know they like maths and would like to know more. The Carnival of Maths is administered by the Aperiodical, and if you’d like to host one on your own blog or see previous editions, you can visit the Carnival of Maths page.

As is traditional, I’ll begin with some interesting properties of this month’s Carnival number, which is 241. It is a prime number, and together with 239 forms one of a pair of twin primes. If you reverse it and add it to itself, you get 241 + 142 = 383, which is also a (palindromic) prime.

On to this month’s submissions! Since it’s been a quiet summer, we’ve combined submissions from June and July to make one big bumper Carnival…

Mathematical Fun and Frivolity

To start us off, Sophia Wood, aka Fractal Kitty, has been playing around with Fibonacci numbers and what happens when you consider them modulo other numbers. The post, titled Modular Fibonacci, starts with a prompt for inquiry, along with some educator resources for running it as an activity in school.

In the previous Carnival, we featured a Mastodon thread from Josh Millard about the ‘Every 5×5 Nonogram‘ website that’s been sucking away people’s time (and they’re almost there – only a few million more to go at time of writing!) To take this one step further, the incredible Matthew Scroggs has investigated whether it’s possible to build a 5×5 nonogram for each letter of the alphabet, and turned it into a font you can use to send slightly inconvenient messages.

If you like football and probability, you may enjoy this short musing from mathematical blog The Bees, in which they discuss the way bookmakers set odds for football matches, and how you might be able to slightly game the system by transforming a hyperbola model into a sigmoid curve model, inspired by reading David Sumpter’s “The Ten Equations that rule the World“.

And still on football, Kit Yates has used the excuse of the men’s UEFA Under-21 Championships to write this blog post about the mathematical coincidences inherent in groups of people teaming up.

In this Mathstodon thread, Craig Kaplan (of monotile fame) discusses how different polyhedral dice roll, inspired by a child’s inquiry.

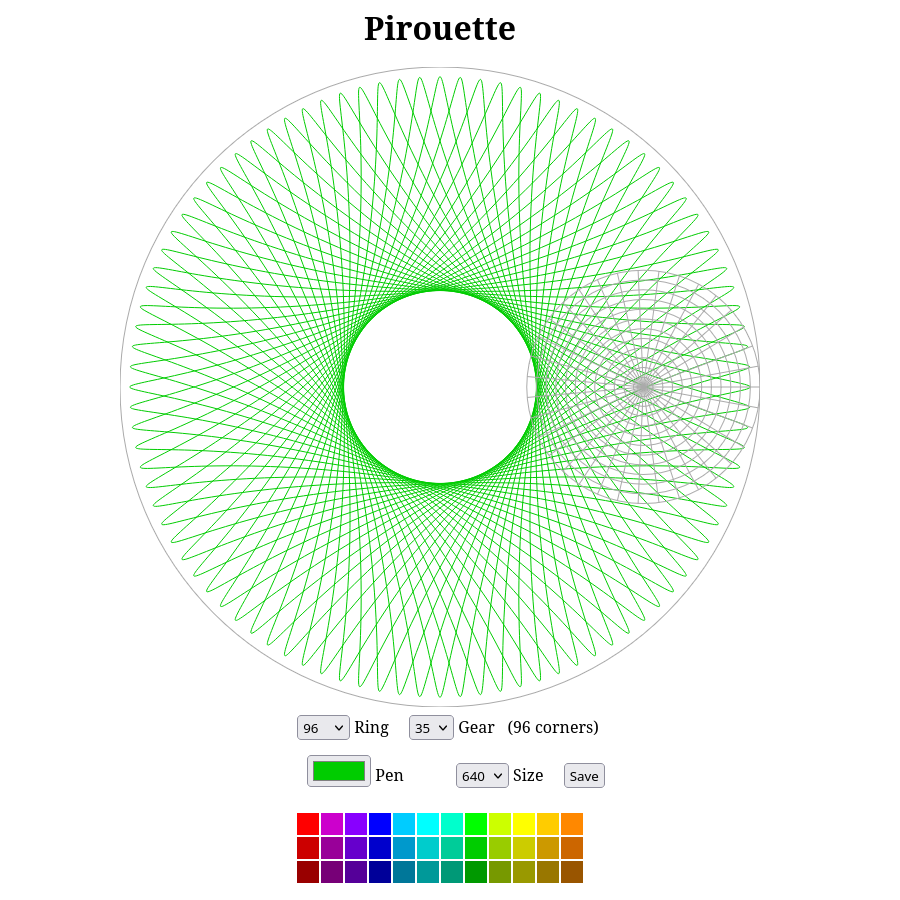
The Diff Geom blog has written a nice outline of their Spirograph clone, Pirouette – including details of how it can be used to produce nice images, and export PNG files. And this blog post from John D Cook explains how classical number theory from the eighteenth century is being used in cryptocurrency smart contracts.

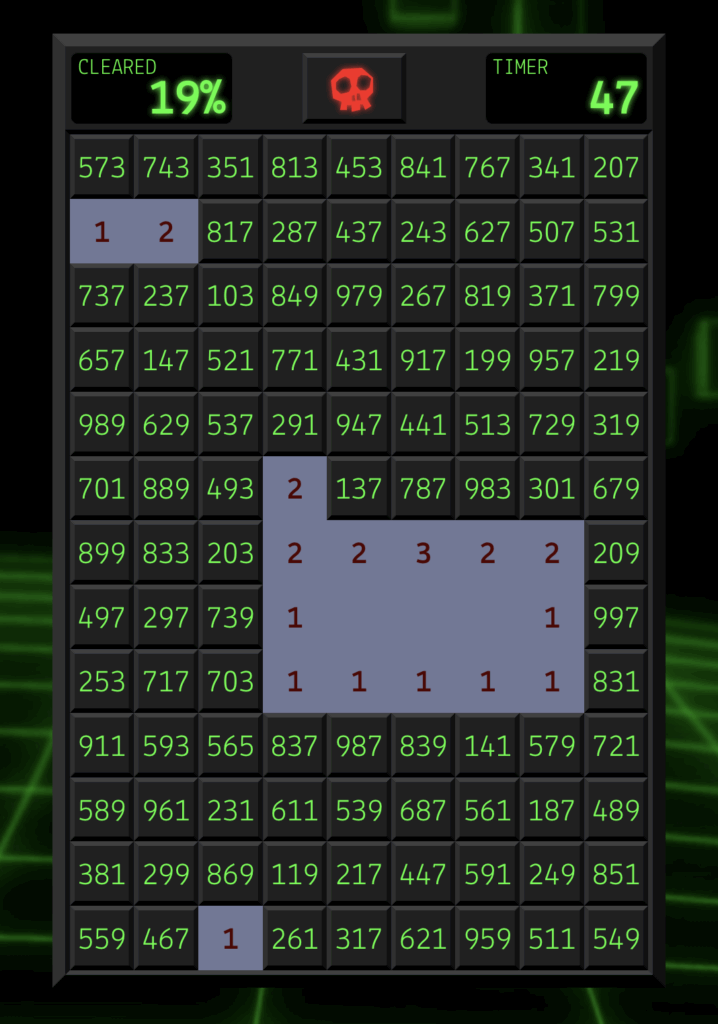
Ever wondered what goes into making an online game? Matt Round has shared this Mastodon thread outlining all the steps he took to build the game PrimeSweeper, a mathematical variant of the game MineSweeper. The attention to detail is phenomenal – including commissioning a Tron-style version of the Windows 95 wallpaper! It turns out the whole thing was inspired by old internet maths favourite, the Prime Number Shitting Bear.

And in honour of the recent pythagorean triple date on 24/7/25 (or 7/24/25 if you prefer), Karen Campe has written a lovely roundup of activities and animations related to the Pythagorean Theorem for you to have your own Pythagorean Party.

Discoveries and Research

One of the many exciting mathematical discoveries this year was a new lower bound on the sixth Busy Beaver number BB(6), which is now confirmed to be flipping humongous. This blog post from Bill Gasarch outlines the consequences of the discovery, and this post on Scott Aaronson’s blog has more detail. And while we’re improving lower bounds on things, Gil Kalai has blogged about an improvement on lower bounds in Ramsey Theory.

There’s also exciting number news: the repunit \(R_{109297}\), consisting of 109,297 ones, which was found to be a probable prime in 2007, was certified as prime on May 25, 2025 by Enge and Underwood, as reported on its PrimePages entry in June by Paul Underwood.

In this week’s New Scientist, you can read about a newly discovered tetrahedron that’s monostable (£) – no matter which way up you place or throw it, it will always return to resting on the same face. If you’d like to read more, there’s also a writeup in Quanta, and the original ArXiV paper about the discovery.

Everything Else

Peters’ blogs have been active this month: this blog post from Peter Cameron’s blog touches on mathematical poetry; and meanwhile Peter Woit’s blog hosts a guest post from Aravind Asok outlining some recent discussions between mathematicians about designing problems to test the reasoning powers of AI, with mixed results.

Bill Gasarch has shared the sad news of Tom Lehrer’s passing, including some lovely anecdotes and memories of Lehrer’s life.

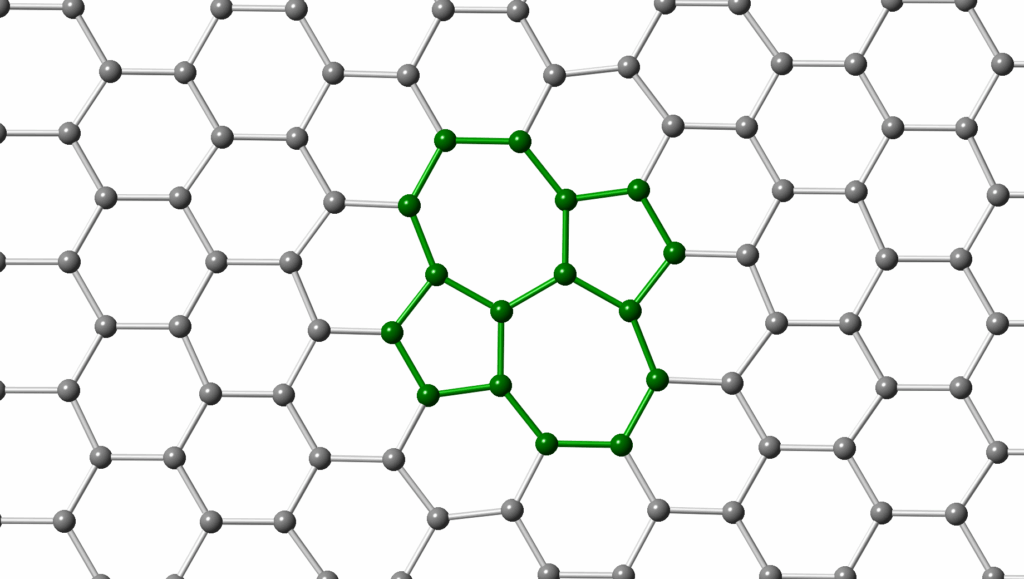
There’s a short blog post from John Baez about the Stone-Wales transformation, a geometrical transformation relevant to chemistry and atomic structures – which can produce defects like the one in graphene shown above. And Skewray research has shared two blog posts, one on Fitting Characteristic function to sampled data, and an accompanying one on optimising with the \(L_\infty\) norm.

Watch out for next month’s Carnival of Maths, which will be posted on Colin Beveridge’s blog, Flying Colours Maths. And if you’re interested in hosting, get in touch by emailing katie@aperiodical.com, or read more about hosting on the Carnival of Maths page.