A conversation about infinity inspired by The Library of Babel by Jorge Luis Borges. Presented by Katie Steckles and Peter Rowlett.
Podcast: Play in new window | Download
Subscribe: RSS | List of episodes
A brief update about the state of social media. A couple of years ago, I wrote about the decline of Twitter and how I was going to consciously shift my activity to Mathstodon. Just over a year ago, we launched The Finite Group, a members’ club for mathsy people, partly inspired by the collapse of social media. We recently updated this to include a free membership.
Since then, I’ve ended up in an awful state where I’m somewhat engaging with X, Mastodon, Bluesky and Threads, but not engaging much with any. If I have something to broadcast, say a new blog post, I’ll put it on all four. If I have something to say or fancy a chat, I might put it on Mastodon. What’s happening just now is that more people seem to have decided to leave X for Bluesky. Will that stick? I don’t know, but it’s nice to see people who I used to see on Twitter being active, and for whatever reason those people haven’t got on with Mastodon, so it seems promising (from that point of view, though it’s not an ideal place to be).
Here’s my current position:
A conversation about mathematics inspired by a very special parallelepiped. Presented by Katie Steckles and Peter Rowlett, with special guest Ayliean.
Podcast: Play in new window | Download
Subscribe: RSS | List of episodes
A conversation about mathematics inspired by an area the size of Wales. Presented by Katie Steckles and Peter Rowlett.
Podcast: Play in new window | Download
Subscribe: RSS | List of episodes
A conversation about election mathematics inspired by a ballot. Presented by Katie Steckles and Peter Rowlett, with special guest Sam Hansen.
For more from Sam and the Carry the Two podcast check out this episode about Mathematics and Voting.
Podcast: Play in new window | Download
Subscribe: RSS | List of episodes
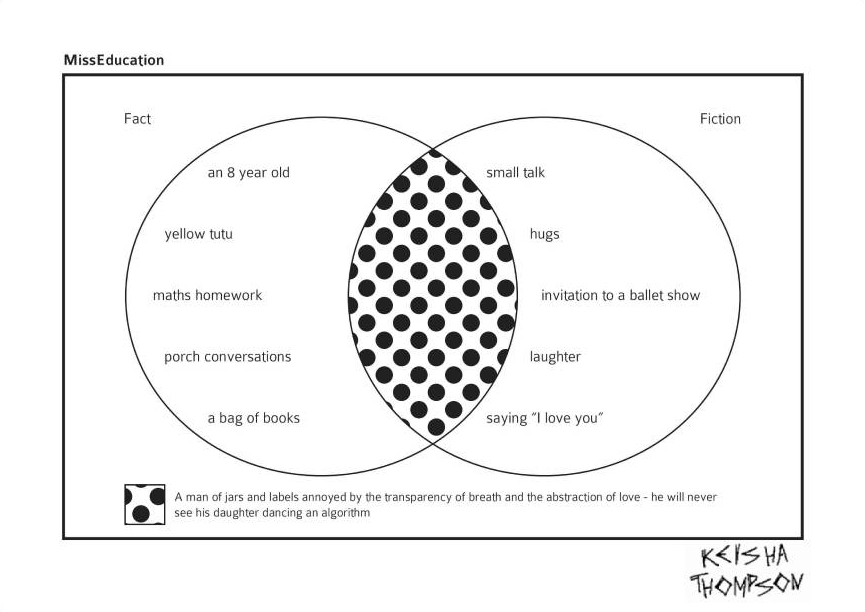
A conversation about mathematics inspired by a space-filling curve. Presented by Katie Steckles and Peter Rowlett.
Podcast: Play in new window | Download
Subscribe: RSS | List of episodes
A conversation about mathematics inspired by a low bridge sign. Presented by Katie Steckles and Peter Rowlett, with special guest Adam Townsend.
The plot discussed around 11 minutes and various other photos are available on Adam’s Height Hunt website (spoilers for the episode’s twists and turns!).
Podcast: Play in new window | Download
Subscribe: RSS | List of episodes