A conversation about mathematics inspired by a low bridge sign. Presented by Katie Steckles and Peter Rowlett, with special guest Adam Townsend.
The plot discussed around 11 minutes and various other photos are available on Adam’s Height Hunt website (spoilers for the episode’s twists and turns!).
Podcast: Play in new window | Download
Subscribe: RSS | List of episodes
Earlier this week I posted a matrix multiplication worksheet on Mastodon.
If you do some of these, you might spot what’s funny about them. For example.
\[ \Large \begin{bmatrix}
\color{navy}{4} & \color{navy}{8}\\
\color{navy}{2} & \color{navy}{3}
\end{bmatrix} \begin{bmatrix}
\underline{\color{blue}{8}} & \underline{\color{blue}{8}}\\
\underline{\color{blue}{2}} & \underline{\color{blue}{7}}
\end{bmatrix} = \begin{bmatrix}
\color{navy}{4}\underline{\color{blue}{8}} & \color{navy}{8}\underline{\color{blue}{8}}\\
\color{navy}{2}\underline{\color{blue}{2}} & \color{navy}{3}\underline{\color{blue}{7}}
\end{bmatrix} \]
That is, the answer to each question can be made by treating the element in the first matrix as the first digit and the corresponding element in the second matrix as the second digit in the answer element. This is not how matrix multiplication works, and ought to be funny if I hadn’t totally over-explained the joke!
I saw one of these in a meme that Katie posted in the Finite Group chat and it got me thinking about how these work.
If we set up the matrices like this
\[ \begin{bmatrix}
a & b\\
c & d
\end{bmatrix} \begin{bmatrix}
e & f\\
g & h
\end{bmatrix} = \begin{bmatrix}
10a+e & 10b+f\\
10c+g & 10d+h
\end{bmatrix} \]
Then we establish four equations with eight unknowns.
\[ \begin{align*}
ae + bg &= 10a+e\\
af+bh &= 10b+f\\
ce+dg &= 10c+g\\
cf+dh &= 10d+h
\end{align*}\]
Since there are more unknowns than equations, these don’t have a single solution. What I wanted was to find integer solutions with all values single-digits. I wrote some Python code to find these. I removed some that look overly symmetrical – either the rows of the matrix are identical, or the same matrix is repeated. This left 73 items.
From these 73 items, I wrote a second Python script that picks 20 of them at random and builds these into a LaTeX worksheet. For the Mastodon post I reformatted this into the shape and size that I thought would display better on social media, and added in one of the squared matrices for an extra hint something weird is up, hoping people might notice this isn’t just a boring post about matrix multiplication practice!
You can view these scripts and associated files on GitHub.
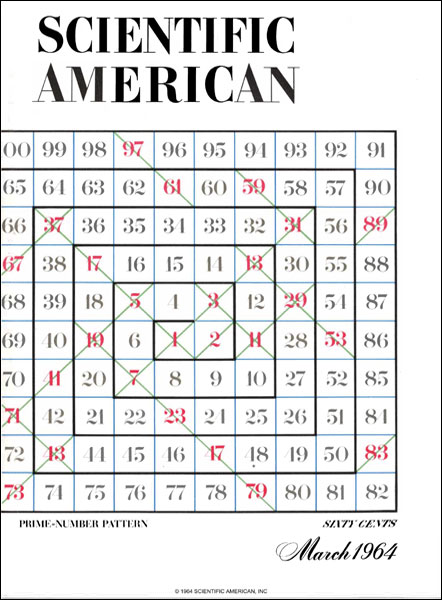
I’m slowly working to (sort of) recreate Martin Gardner’s cover images from Scientific American, the so-called Gardner’s Dozen.
This time it’s the turn of the March 1964 issue. In the article ‘The remarkable lore of the prime numbers’, later included as chapter 9 in Martin Gardner’s Sixth Book of Mathematical Games from Scientific American, Gardner describes how Stanislaw Ulam in a boring meeting doodled a grid of numbers, spiralling out, then circled the primes. “To his surprise the primes seemed to have an uncanny tendency to crowd into straight lines.” These Ulam sprials, discovered the year before, contain lines related to prime-generating functions, which I have written about recently.
The UK Government have announced the new set of King’s Birthday Honours. Here’s our selection of particularly mathematical entries for this year. If you spot any more, let us know in the comments and we’ll add to the list.
Get the full list from gov.uk. Spot anyone we’ve missed? Let us know in the comments.
A few weeks ago I heard someone casually refer to ‘that formula of Euler’s that generates primes’. I hadn’t heard of this, but it turns out that in 1772 Euler produced this formula:
\[ f(x) = x^2 + x + 41\text{.} \]
Using this, \(f(0)=41\), which is prime. \(f(1)=43\), which is also prime. \(f(2)=47\) is another prime. In fact this sequence of primes continues for an incredible forty integer inputs until \(f(40)=41^2\). It might generate more primes for higher inputs, but what’s interesting here is the uninterrupted sequence of forty primes.
This got me wondering. Clearly \(f(0)\) is prime because 41 is prime, so that much will work for any function
\[ f(x) = x^2 + x + p \]
for prime \(p\), since \(f(0)=0^2+0+p=p\). Are there other values of \(p\) that generate a sequence of primes? Are there any values of \(p\) that generate longer sequences of primes?
I wrote some code to investigate this. Lately, I’ve taken to writing C++ when I need a bit of code, for practice, so I wrote this in C++.
I figured the cases where \(f(0)\) is prime but \(f(1)\) isn’t weren’t that interesting, since \(f(0)\) is trivially prime. In fact, \(f(x)=x g(x)+p=p\) when \(x=0\) for any prime \(p\), but saying so doesn’t seem worth the effort.
So I kept track of the primes \(p\) whose functions \(f(x)=x^2+x+p\) generate more than one prime, and the lengths of the sequences of primes generated by each of these. This produced a pair of integer sequences.
I put the primes that work into the OEIS and saw that I had generated a list of the smaller twin in each pair of twin primes. I was momentarily spooked by this, until I realised it was obvious. Since \(f(0)=p\) and \(f(1)=1^2+1+p=p+2\), any prime this works for will generate at least a twin prime pair \(p,p+2\).
What about the lengths of the sequences of consecutive primes generated? The table below shows the sequences of consecutive primes generated for small values of \(p\). Most primes that generate a sequence produce just two, and \(p=41\) definitely stands out by generating forty.
| \(p\) | \(f(x)\) | Primes generated | Number of consecutive primes generated |
| 3 | \(x^2+x+3\) | 3, 5 | 2 |
| 5 | \(x^2+x+5\) | 5, 7, 11, 17 | 4 |
| 11 | \(x^2+x+11\) | 11, 13, 17, 23, 31, 41, 53, 67, 83, 101 | 10 |
| 17 | \(x^2+x+17\) | 17, 19, 23, 29, 37, 47, 59, 73, 89, 107, 127, 149, 173, 199, 227, 257 | 16 |
| 29 | \(x^2+x+29\) | 29, 31 | 2 |
I was pleased to see this sequence of lengths of primes generated was not in the OEIS. So I submitted it, and it is now, along with the code I wrote. (I discovered along the way that the version where sequences of length one are included was already in the database.)
Anyway, I amused myself by having some C++ code published, and by citing Euler in a mathematical work. Enjoy: A371896.
With the emphasis on occasionally, I’m occasionally working to (sort of) recreate Martin Gardner’s cover images from Scientific American, the so-called Gardner’s Dozen.
This time I’m looking at the cover image from the November 1959 issue. The column is ‘How three modern mathematicians disproved a celebrated conjecture of Leonhard Euler’, about the so-called Euler’s Spoilers, the story of three mathematicians – Parker, Bose and Shrikhande – who had disproved a conjecture of Euler’s about Latin squares. The column was reprinted as chapter 14 in his New Mathematical Diversions from Scientific American.
A few months ago a group of us launched a membership club, The Finite Group, which you can join!
A big update is the lineup — your membership now supports the work of and gives you access to content from mathematician and TikTok star Ayliean MacDonald, as well as Chalkdust’s Matthew Scroggs and The Aperiodical’s Katie Steckles and me. Membership gives you access to a chat community and monthly livestreams. For a taste of the livestreams, check out this π minute video!
The big news is that the next livestream will be free to view live online on 27th March from 5-6pm GMT. All four of us will be working through the recent ‘100 Mathematical Conventions Questions’ quiz that’s been dividing (a small subset of) the internet. The stream will be available live, and a recording will be available to members afterwards.