I recently had an idea: map the Unix time (seconds since 1st January 1970) to shufflings of a deck of cards. Each second would correspond to a different ordering of the 52 cards.
I wanted to think about how mind-bogglingly huge $52!$ is: $52!$ seconds is more than $2 \times 10^{60}$ years. So even if you spent your entire life watching this thing, you’d leave this world having seen basically none of the possible permutations. Happily, Wikipedia reckons that the heat death of the universe will happen in about $10^{100}$ years, so there’s plenty of time for me to enact my plan.
Recently someone on Twitter, and then two people on US cable news, said that Michael Bloomberg could have used the \$500 million he spent on his presidential campaign to give everyone in the USA \$1 million. This caused quite a fuss.
In short, someone divided 500 by 327, saw that the answer was bigger than 1 and the units were “millions”, and concluded that the money could instead have been distributed to give everyone \$1 million.
That’s an easy mistake to make for someone writing a tweet, but the kind of error that should have made someone think “does that make sense?” before planning a segment on TV news about it.
It’s raised a couple of interesting questions, though:
If that money was shared between every American citizen, how much would each one get?
If Michael Bloomberg wanted to give \$1 million to everyone in a smaller area, where could he choose?
I realised that all the data I need is freely available on the internet, so I made a website to do the calculations for you:
It asks you how much money you’ve got, then for every power of 10 dollars, it tells you where in the USA you could give every resident that much.
To give you an idea of how far the net worths of people like Michael Bloomberg could go, it’s got a list of shortcuts for billionaires. Appropriately, I got that data from Bloomberg’s own website. Bloomberg himself was mysteriously missing from the list, so I got his net worth from Google and added it in myself.
The most unexpected thing for me was seeing how much money these people would have left over after giving everyone in the USA \$100. They’d still be enormously, unimaginably rich!
I’ll describe a few of the fiddly details of the implementation now. At first the “how much money have you got?” input was a text field, but I realised it’d be much better to have a slider that you can swing from \$1 all the way up to \$1 trillion. It’s a logarithmic scale, so powers of 10 are equally spaced.
I got data on the populations of US cities and states from data.census.gov.
Working out which amounts and places to show you wasn’t completely straightforward. I thought it’d be easiest to fix the amounts given away to a power of 10 per person, and to find places where the population meant that the amount left over would be as small as possible. To do that, my code works through the list of places in ascending order of population, and stops at the last place whose population is big enough to give everyone at least the target amount.
I enjoyed making this tool, and I hope it helps somebody get a better feel for what these big numbers mean.
While I’m on strike, I’m catching up on stuff I’ve made but never posted about here.
At the Talking Maths in Public conference last August, I was talking with Katie Steckles and Kevin Houston about the order of operations. I think that another one of those ambiguously-written sums had gone round Twitter again. I said it would be good to have a tool where you can write an expression, then change the order of operations and see what happens.
So, on the way home, I wrote one! I’ve called it SAMDOB, which is an anagram of BODMAS.
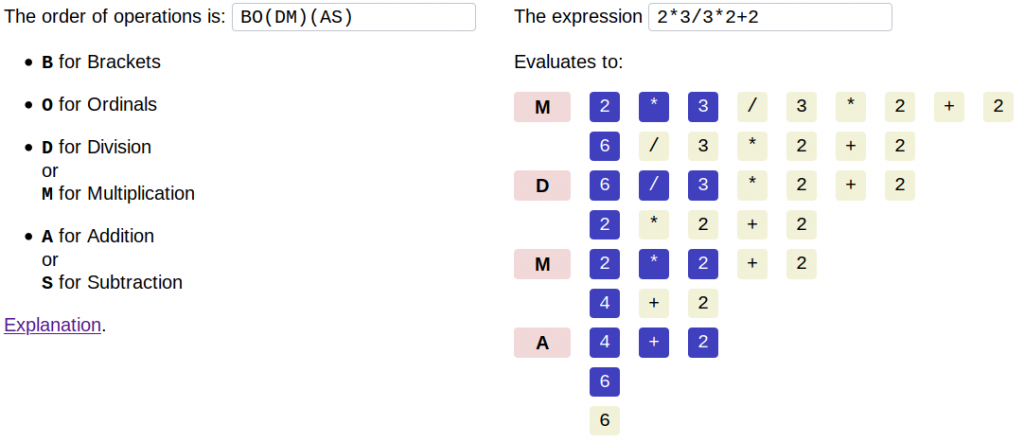
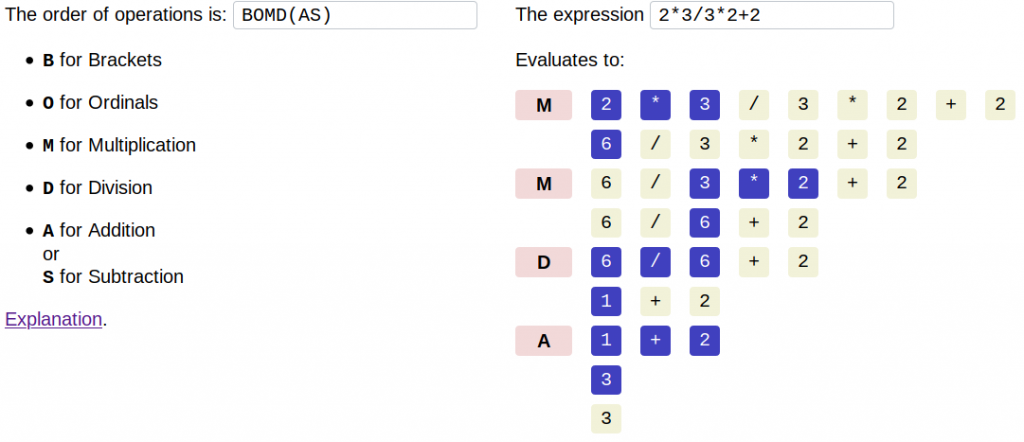
Please have a play with it. I can imagine that this could be useful to people teaching the order of operations in real life. Let me know if you have any suggestions for improvements.
Last year I wrote about a 3D-printed puzzle I’d designed, called Seven Triples.
At work we want to use this puzzle during an A-Level enrichment day, which means we need about twenty copies of it. I 3D-printed four copies over the course of a couple of weeks, in amongst other jobs, and I don’t have the patience to do any more. So, I’ve made a 2D version that we can print and cut out much more quickly.
At work we’ve got a 3D printer. In this series of posts I’ll share some of the designs I’ve made.
This is something I’ve wanted to make for a long time: a literal sieve of Eratosthenes.
This is a collection of trays which stack on top of each other.
Each tray has a grid of holes, with some holes filled in. The tray with a “2” on it has every second hole filled in; the tray with a “3” has every third hole filled in; and so on.
When the trays are stacked together, the holes you can see through correspond to prime numbers: every other number is filled in on one of the trays.
I went through quite a few iterations of this design. The first version was a series of nesting trays. After printing it, I realised that you might want to put the trays in a different order. After that, I did a lot of fiddling with different ways of making the plates stack on top of each other. The final version has sticky-outy pegs at each corner, and corresponding holes on the other side. I had to add a fair bit of margin around the holes so the wall didn’t go wiggly when printed.
At work we’ve got a 3D printer. In this series of posts I’ll share some of the designs I’ve made.
At the start of the Summer we (I) bought a new 3D printer for the department, a FlashForge Dreamer. It’s got two extruder heads, so it can do two-colour prints.
To test that out, I designed this Golomb ruler. It’s a straightedge with marks at 0, 1, 4 and 6 cm. The idea is that you can measure 1, 2, 3, 4, 5 or 6 cm by lining up against different pairs of marks. I recently did a silly Twitter thread on this subject.
As you can see from the photo, two-colour printing isn’t quite as straightforwared as it could be. Because both nozzles need to stay hot, while one colour was printing the other just oozed out and made a mess. There are some settings on the printer you can change to try to reduce this, but I haven’t got the hang of it yet.
