The nice chaps at Kitki, an educational board game company based in India, have come up with a cool idea for a mathematical board game. They’re funding it through IndieGoGo (which if you haven’t heard of it is a bit like Kickstarter), and they’re looking for your help.
Theorem: You can turn any shape into a rabbit by adding a face, ears and a tail to it.
Proof (by construction): geobunnies.com
This is delightful. There’s a new school of Platonism, one which believes that not only do ideal shapes exist, so do the bunnies inside them.
Joy!
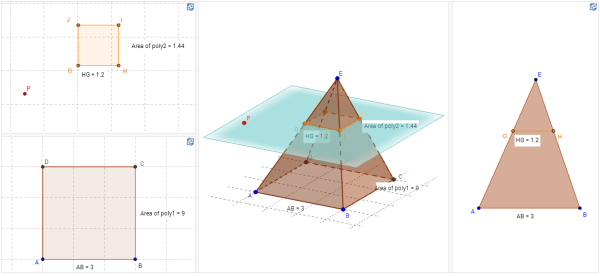
Recently Tim Hutton and Adam Goucher have been playing around with hyperbolic tesselations. That has produced a {4,3,5} honeycomb grid for the reaction-diffusion simulator Ready, which Adam talked about on his blog a couple of days ago. Tim has also made a much simpler toy to play with in your browser: a visualisation of mirror tilings (the Wythoff construction) in spaces with different curvatures.
Hyperplay lets you select the kind of regular polygon you want to tile, and then your mouse controls the curvature of the space it sits in. Certain curvatures produce exact tilings of the space – for example, triangles tile a space with zero curvature – and you get projections of polyhedra for certain positive curvatures.
GeoGebra, the Aperiodical’s official Favourite Thing for Messing About With Geometry, has just bumped up to version 5. With that bigger number comes another dimension – GeoGebra now supports three-dimensional geometry!
George Hart is putting on a one-man show of his sculptures at Stony Brook University. He’s posted this video of him walking through the exhibition and describing the pieces on display.
[youtube url=https://www.youtube.com/watch?v=DI1612YhMqg]
George also gave a lecture to open the exhibition, which you can watch on the SCGP website.
Euclid’s Kiss: Geometric Sculpture of George Hart is on display at the Simons Center for Geometry and Physics during September and October.
More information: Euclid’s Kiss: Geometric Sculpture of George Hart
Yet another fun toy for you. Give a computer a set of tiles defined by what their edges look like, can you fit them together? That problem is undecidable, since you can encode Turing machines as sets of tiles, but it turns out it’s fun to watch a computer try.
Ghost Diagrams asks you for a set of tiles (or it’ll make some up if you didn’t bring one) and shows you its attempts to make them fit together. It’s very pretty, and quite mesmerising. Sometimes it looks even better when you turn on the “knotwork” option.
Paul Harrison created Ghost Diagrams while writing his PhD thesis, Image Texture Tools: Texture Synthesis, Texture Transfer, and Plausible Restoration. He’s written a short blog post about the program.
Here are a few patterns I liked: 1, 2, 3, 4, 5.
via John Baez on Google+.
This is a fun game to while away the midweek blues. You’re presented with two dots. You can drag between dots to create lines and circles, as if you had a straightedge and compass. Apart from a few challenges to get you thinking, that’s pretty much it!
The game was created by Nico Disseldorp, who has a few more fun things on his website, Science vs Magic.
Play: ANCIENT GREEK GEOMETRY