Welcome to the 241st Carnival of Mathematics, hosted here at the home of the Carnival, The Aperiodical. The Aperiodical is a shared blog written and curated by Katie Steckles (me), Christian Lawson-Perfect and Peter Rowlett, where we share interesting maths news and content, aimed at people who already know they like maths and would like to know more. The Carnival of Maths is administered by the Aperiodical, and if you’d like to host one on your own blog or see previous editions, you can visit the Carnival of Maths page.
You're reading: Posts Tagged: pythagoras
- Multiply the first and the last numbers $\rightarrow 3 \times{13}=39$
- Multiply then double the middle two numbers $\rightarrow 5 \times{8}\times{2}=80$
- Sum the squares of the middle two numbers $\rightarrow 5^{2}+8^{2}=89$
- The Pythagorean triple is $(39, 80, 89) \rightarrow 39^{2}+80^{2}=7921=89^{2}$
- The Euclidean distance formula and it’s extension to higher dimensions
- The Pythagoreans and music – Donald Duck in Mathmagic Land
- Biography search of included mathematicians
- 2 High School Students Prove Pythagorean Theorem – proof awaiting verification
- Pythagorean trigonometric identities
- The latest Mersenne prime and a Pythagorean triple
- Related themes – Legendre’s three-square theorem and Fermat’s theorem on sums of two squares
Hidden in Plane Sight
This is a guest post by Elliott Baxby, a maths undergraduate student who wants to share an appreciation of geometrical proofs.
I remember the days well when I first learnt about loci and constructions – what a wonderful thing. Granted, I love doing them now; to be able to appreciate how Euclid developed his incredible proofs on geometry.
Pythagoras and his theorem
In this guest post, David Benjamin shares a cornucopia of concepts and stories relating to Pythagoras and his famous theorem.
I admit to mild irritation when I’m told that Pythagoras’ theorem is $a^2+b^2=c^2$. The theorem is based on area – in particular, that of squares. There are many proofs of the theorem and in this post we present a miscellany of Pythagorean Theorem curiosities, including some of my favourite proofs, the theorem’s links to algebra, geometry and number theory, an assassination of a president of the USA, an alleged murder in Greece, an infinite spiral of surds, Gauss and coordinate geometry – plus another connection between Pascal and Fibonacci.
The theorem
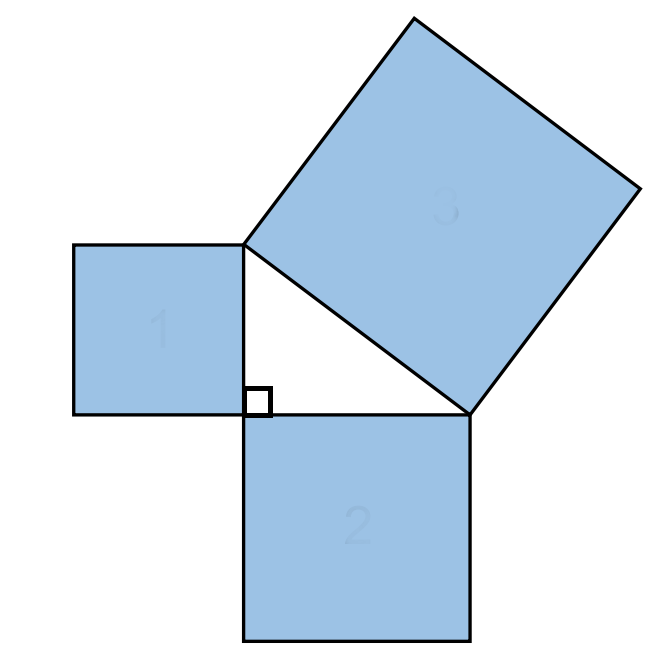
A square is added to each side of a right-angled triangle as shown in the above image. The sum of the the areas of the two smaller squares is equal to the area of the largest square. If the hypotenuse of the triangle has a length of $c$ and the other two sides are of length $a$ and $b$ then $a^2+b^2=c^2$
When the length of each side of the triangle is a positive integer, the three numbers make a Pythagorean triple. $(3, 4, 5)$ is the smallest triple with $3^2+4^2=5^2$. The Chinese text Chou Pei Suan Ching – original title Zhoubi – (周髀算经), (The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven) gives this visual proof for the $(3, 4, 5)$ triple.
$(3, 4, 5)$ is a primitive triple since $3, 4$ and $5$ are coprime – their only common divisor is $1$. $(n\times3, n\times4, n\times5), n = 2, 3, 4,…$ are part of the same ‘family’ and clearly not primitive triples. Another primitive triple is $(5, 12, 13)$ and an ordered sequence of hypotenuses for such triples are listed here. In the sequence I was surprised to see $185$ appearing twice. In fact there are exactly four distinct triples with hypotenuse $185$. With the aid of a spreadsheet, I was able to find them: $(57, 176, 185), (60, 175, 185),(104, 153, 185)$ and $(111, 148, 185)$
Generating Pythagorean triples
The sequence $\frac{1}{1},\frac{3}{2},\frac{7}{5},\frac{17}{12},\frac{41}{29},\frac{99}{70},\frac{239}{169},\frac{577}{408},\frac{1393}{985},…$ produces a Pythagorean triple from every other term beginning with $\frac{7}{5}$:
$\frac{7}{5}=\frac{3+4}{5} \rightarrow 3^2 + 4^2 = 5^2$
$\frac{41}{29}=\frac{20+21}{29} \rightarrow 20^2 + 21^2 = 29^2$
$\frac{239}{169}=\frac{119+120}{169} \rightarrow 119^2 + 120^2 = 169^2$
$\frac{1393}{985}=\frac{696+697}{985} \rightarrow 696^2 + 697^2 = 985^2$
…
As an added bonus, the decimal equivalent of each term of the sequence converges to $\sqrt2$, in a similar way the Fibonacci sequence converges to the golden ratio $\psi=\frac{1+\sqrt5}{2}$
Another method to find Pythagorean triples uses consecutive even numbers and the sum of their reciprocals as shown below.
Choose any pair of consecutive even numbers:
$8$ and $10$ $\rightarrow \frac{1}{8} + \frac{1}{10} = \frac{9}{40} \rightarrow 9^2 + 40^2 = 1681 = 41^2$
$12$ and $14$ $\rightarrow \frac{1}{12} + \frac{1}{14} = \frac{13}{84} \rightarrow 13^2 + 84^2 = 7225 = 85^2$
$20$ and $22$ $\rightarrow \frac{1}{20} + \frac{1}{22} = \frac{21}{220} \rightarrow 21^2 + 220^2 = 48841 = 221^2$
Euclid of Alexandria (325BC – 265BC) was a Greek mathematician who wrote a treatise, The Elements – a collection of 13 books. Books 1 to 6 are on plane geometry and books 7 to 9 on number theory. Euclid created a formula for generating Pythagorean triples from any pair of positive integers $m$ and $n$, where $m>n$:
($m^2-n^2, 2mn, m^2+n^2$) is the triple.
If $m=7$ and $n=3$, the triple is ($40, 42, 58$) $\rightarrow 40^2 + 42^2 = 3364 = 58^2$
If $m=89$ and $n=11$, the triple is ($7800, 1958, 8042$) $\rightarrow 7800^2 + 1958^2 = 64673764 = 8042^2$
A lovely link between Pascal, Fibonacci, Euclid and Pythagoras comes via any four consecutive Fibonacci numbers
| $F_{1}$ | $F_{2}$ | $F_{3}$ | $F_{4}$ | $F_{5}$ | $F_{6}$ | $F_{7}$ | $F_{8}$ | $F_{9}$ | $F_{10}$ |
| $1$ | $1$ | $2$ | $3$ | $5$ | $8$ | $13$ | $21$ | $34$ | $55$ |
Using $3, 5, 8, 13$
$F_{1}$ to $F_{4}$ gives the primitive triple $(3, 4, 5)$
$F_{2}$ to $F_{5}$ gives the primitive triple $(5, 12, 13)$
$F_{3}$ to $F_{6}$ gives the triple $(16, 30, 34)$
$F_{7}$ to $F_{10}$ gives the primitive triple $(715, 1428, 1597)$
In addition, for any set of four consecutive Fibonacci numbers, $F_{7}$ to $F_{10}$ for example, the following connection is true
$7+10=17$ and the $17^{th}$ Fibonacci number is $1597$, the third member of the triple, the hypotenuse of the triangle!
Amazingly, if we use $m$ and $n$ as consecutive Fibonacci numbers when using Euclid’s method, then the last number of the triple is again a Fibonacci number
| $m$ | $n$ | Triple | Fibonacci number |
| $2$ | $1$ | $(3, 4, 5)$ | $5^{th}$ |
| $3$ | $2$ | $(5, 12, 13)$ | $7^{th}$ |
| $5$ | $3$ | $(16, 30, 34)$ | $9^{th}$ |
| $8$ | $5$ | $(39, 80, 89)$ | $11^{th}$ |
| $13$ | $8$ | $(105, 208, 233)$ | $13^{th}$ |
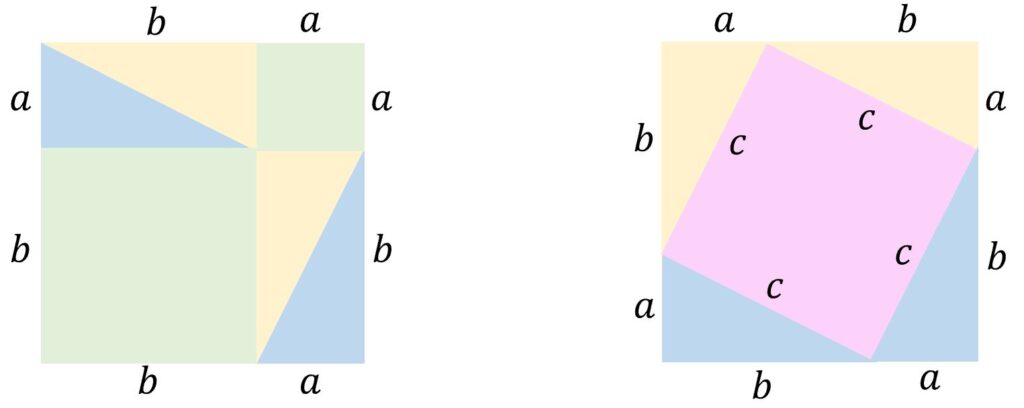
A visual proof of the theorem
I first came across a visual proof of Pythagoras’ theorem for all right-angled triangles in Roger B. Nelsen’s wonderful book Proofs Without Words, Exercises in Visual Thinking. Nelsen noted the proof (author unknown, circa B.C. 200?) is adapted from the Chou Pei Suan Ching. The two images below combine to show the proof:
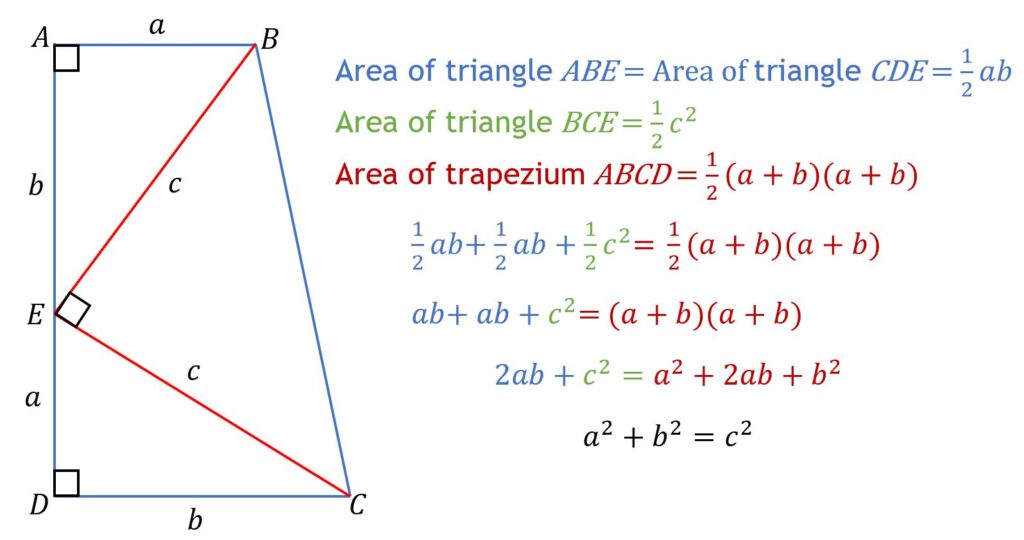
A proof by trapezium area and an untimely painful death
James Garfield (November 19, 1831 – September 19, 1881) was elected as the United States’ 20th President in 1880. He was assassinated after just 200 days in office after being shot on July 2, 1881, in a Washington railroad station. Garfield remained mortally wounded in the White House for many weeks where Alexander Graham Bell, inventor of the telephone, attempted to locate the bullet with an induction-balance electrical device which he had designed. Bell and physicians were unsuccessful in their attempts and Garfield died from an infection and an internal haemorrhage on September 19, 1881.

In 1876, Garfield had an elegant proof of Pythagoras’ theorem published. The proof makes use of the formulae for the areas of a triangle and a trapezium. The proof is demonstrated in the image below
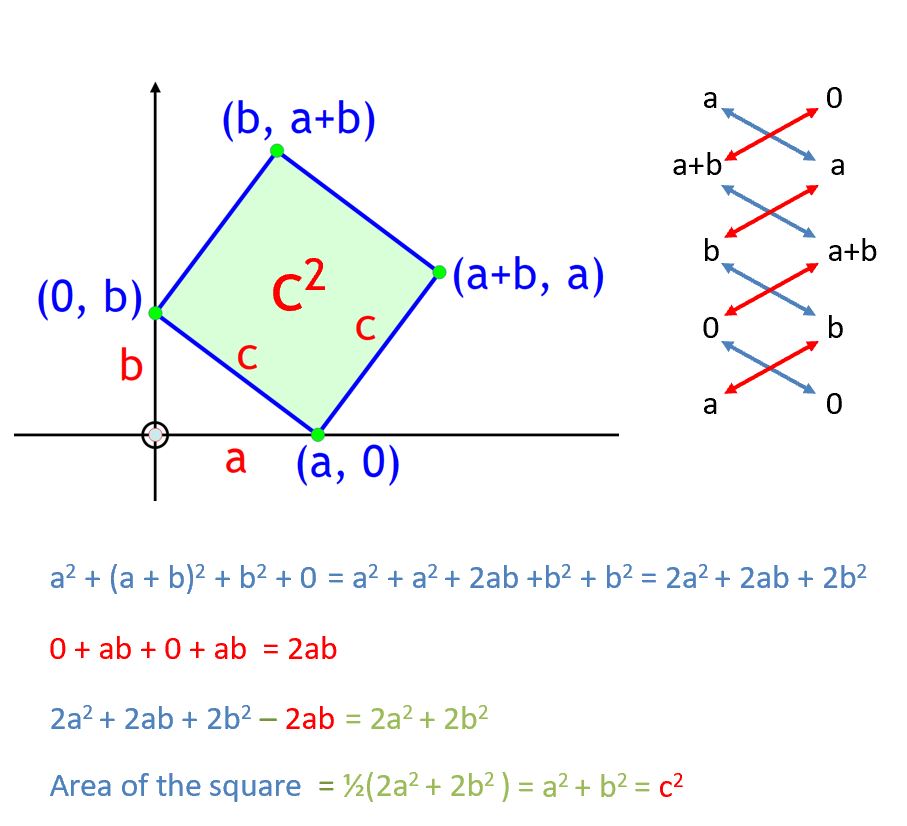
A proof using the Shoelace formula
The brilliant German mathematician Johann Carl Friedrich Gauss (30 April 1777 – 23 February 1855) developed a formula to calculate the area of a polygon if every vertex of the polygon lies on a known Cartesian coordinate. The formula is widely known as the Shoelace formula and makes use of the calculation to find the determinant of a 2 by 2 matrix.
John Molokach observed that the Pythagorean theorem follows from Gauss’ Shoelace Formula, as shown below
It’s not just squares
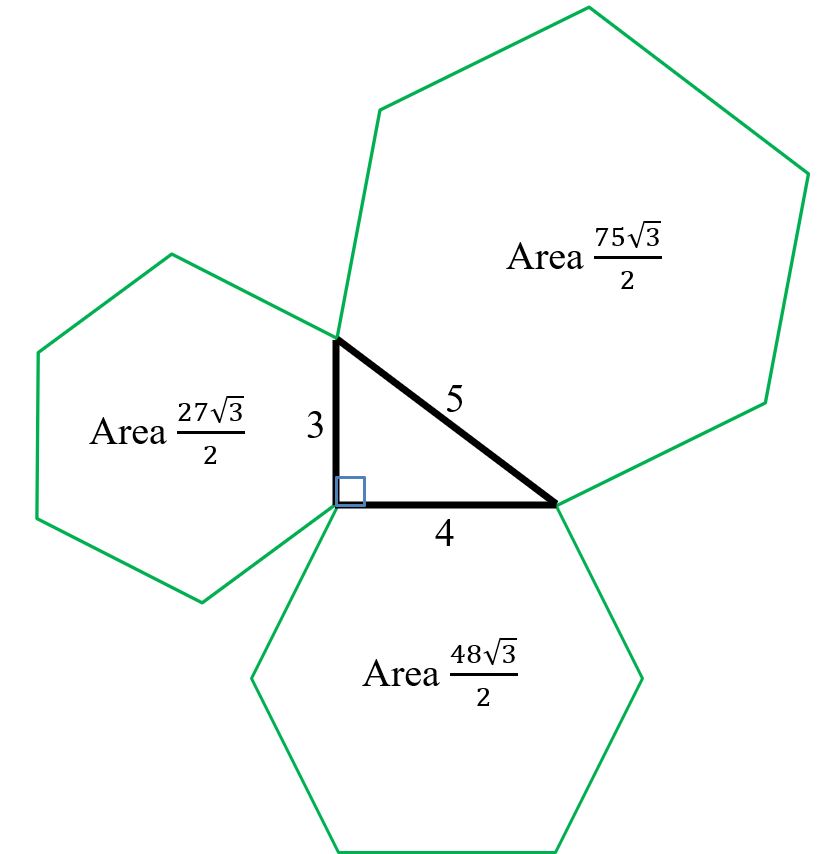
If the same regular $n$-gon, $n$ = 3, 4, 5,.. is drawn on each side of a right-angled triangle, then the sum of the areas of the two smaller $n$–gons equals the area of the $n$–gon on the hypotenuse. Semicircles also produce the same result. As $n\rightarrow \infty$, a regular $n$-gon approaches a circle and so circles, where the sides of the triangle act as tangents to the circles can be said to satisfy Pythagoras’ theorem. The same result can be obtained by rotating the semicircles through $180^ \circ$ and adding matching semicircles.
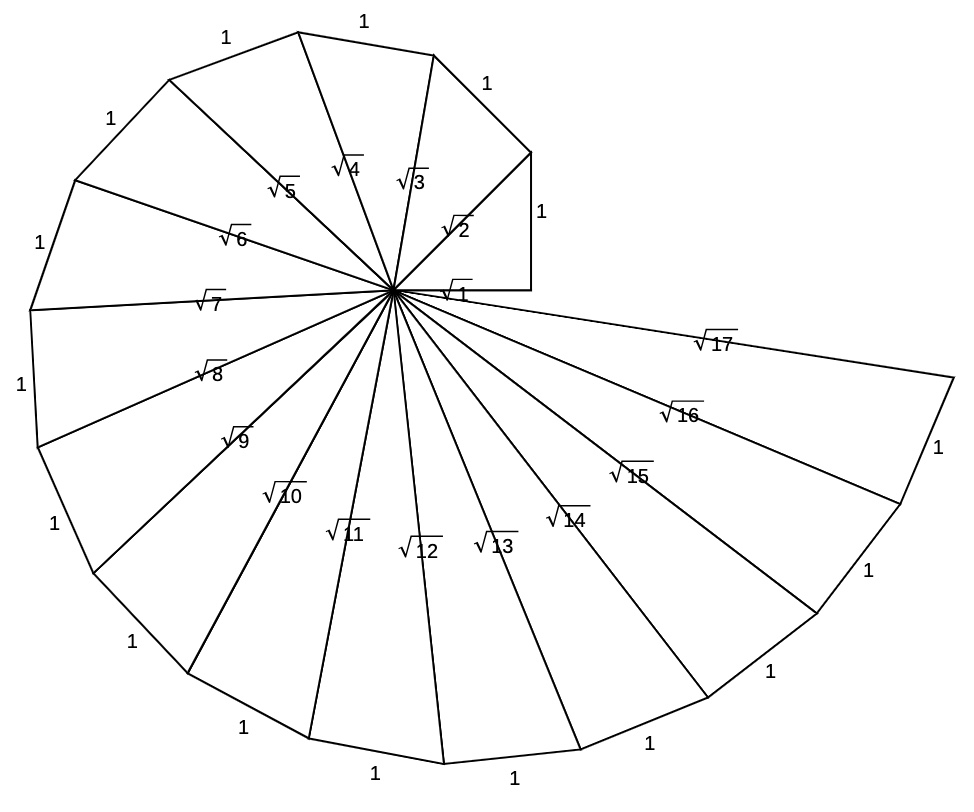
The spiral of Theodorus of Cyrene
When $n$ is not a square number, $\sqrt{n}$ is called a surd
Pythagoras and his followers, the Pythagoreans, believed that the universe can be explained by whole numbers and the ratio of whole numbers. Their moto – “All is number” – was carved above the entrance of their meeting place. However, a spanner was thrown in the works when Hippasus of Metapontum, one of the Pythagoreans suggested that $\sqrt2$, the length of the hypotenuse of the right-angled triangle with sides $1, 1$ and $\sqrt2$, could not be written as the ratio of two whole numbers. Such numbers are now called irrational and it was approximately 200 years before Euclid of Alexandria proved $\sqrt2$ was irrational. The Pythagoreans were sworn to secrecy and one legend suggests that Hippasus was thrown off a boat and drowned for revealing his discovery to non-Pythagoreans. Then again, some believe Hippasus drowned because he revealed how to construct a dodecahedron inside a sphere. The ($1, 1$,$\sqrt2$) triangle is the start of the spiral of Theodorus. Further right-angled triangles, each containing a side of length $1$ unit, are added sequentially to produce the sequence $\sqrt2, \sqrt3, \sqrt4, \sqrt5,…$. The sequence is the length of each new hypotenuse, as shown in the diagram below. Theodorus probably stopped at $\sqrt17$ as it the length of the hypotenuse of the triangle before the triangles begin to overlap. The spiral can be expanded here.
Further reading
Mathematical Stocking Fillers
Looking for small/inexpensive items to put inside a piece of festive footwear (or, to keep for yourself)? Here’s a selection of things we’ve seen lately that you might want to buy! All the items we’re showing are under £20, and range from slightly mathematical to very mathematical.
Mathematical Objects: Pythagoras T-shirt

A conversation about mathematics inspired by a t-shirt featuring Pythagoras’ theorem. Presented by Katie Steckles and Peter Rowlett.

Podcast: Play in new window | Download
Subscribe: RSS | List of episodes
Mathematical myths, legends and inaccuracies: some examples
I’m teaching a first-year module on the history of mathematics for undergraduate mathematicians this term. In this, I’m less concerned about students learning historical facts and more that they gain a general awareness of history of maths while learning about the methods used to study history.
Last week, I decided I would discuss myths and inaccuracies. Though I am aware of a few well-known examples, I was struggling to find a nice, concise debunking of one. I asked on Twitter for examples, and here are the suggestions I received, followed by what I did.
Pictorial proofs
I received this message from Alan Stevens, Nottingham Maths Jam attendee. I am putting it here so readers of this blog and the other Maths Jams might consider the topic as well.
Although I won’t be able to make the next MathsJam at Nottingham I’ve thought of a theme you might like to consider. I don’t know if you have themes, but, if you do, how about “Pictorial proofs and derivations”?
Probably the most obvious pictorial proof is of Pythagoras’s theorem (in fact there are probably several such). Do your mathsjammers know of any more?
I thought of this while viewing James Tanton’s YouTube channel, where he has a very pictorial way of looking at maths, including a very nice pictorially based derivation of the geometric series 1/3 + 1/3^2 +1/3^3 + … = 1/2.
If you haven’t seen someone in a t-shirt displaying a pictorial proof of Pythagoras, you haven’t been going to the right sort of conferences! The James Tanton video reminds me of a pictorial demonstration of summing 1/2 + 1/4 + 1/8 + … which I used in a lecture, after Zeno’s paradox of Achilles and the tortoise, when I was trying to get across the idea of an infinite series summing to a finite amount. Shading half a square, then a quarter, then an eighth, and so on it looks like you will eventually shade the whole square and nothing more, a useful illustration that the series converges to one. In fact, I repeated this in the micro-teaching session of my Postgraduate Certificate in Higher Education course and a screenshot of the slide after I drew on it using the interactive whiteboard is below. I’m not sure if this constitutes a proof, though.