This is the fourth in a series of guest posts by David Benjamin, exploring the secrets of Pascal’s Triangle.
Triangles and fractals
If we highlight the multiples of any of the Natural numbers $\geq 2$ in Pascal’s triangle then they create a pattern of inverted triangles.
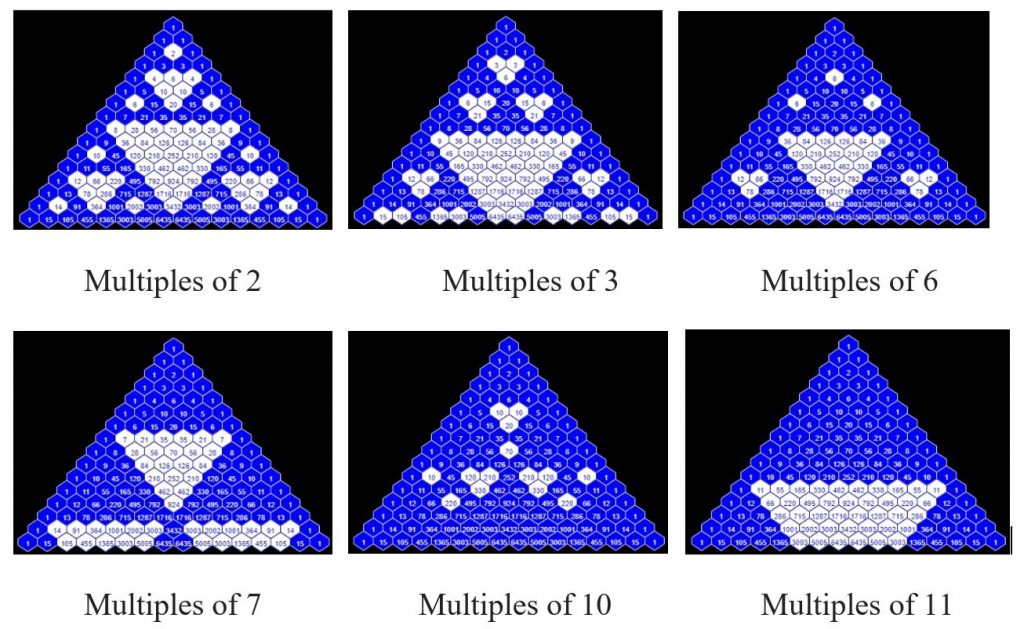
The images above are evocative of the Sierpinski sieve (also known as the Sierpinski gasket or Sierpinski’s triangle), a fractal described in 1915 by the Polish mathematician Waclaw Sierpiński (1882-1969).
Fractals are beautiful geometric shapes. Small, even down to (theoretically) infinitesimal areas of a fractal are identical to the entire shape. The Koch snowflake, generated geometrically by successive iterations on an equilateral triangle, is an example of a fractal. Julia sets and Mandelbrot sets are examples of fractals generated using recursion on complex functions. Many examples of fractals appear in nature, and the Polish-born French-American polymath Benoit Mandelbrot (1924-2010) suggested that fully developed turbulent flows are fractals.
It is a lovely surprise to discover that a simple fractal can be found inside Pascal’s triangle. It is achieved by considering all the numbers in the triangle modulo 2 – equivalent to colouring in only the multiples of 2, as in the first diagram at the top of the post. In this version, every odd number becomes $1$ and every even number becomes $0$, and by considering sufficiently many lines of the triangle, the Sierpinski pattern emerges.
Number patterns in the triangle
If we consider the first 32 rows of the mod$(2)$ version of the triangle as binary numbers: $1, 11, 101, 1111, 10001,…$ and convert them into decimal numbers, we obtain the sequence:
\[1, 3, 5, 15, 17, 51, 85, 255, 257, 771, 1285, 3855, 4369, 13107, 21845, 65535, 65537, \]
\[196611, 327685, 983055, 1114129, 3342387, 5570645, 16711935, 16843009, \]
\[50529027, 84215045, 252645135, 286331153, 858993459, 1431655765, 4294967295\]
Interestingly, all members of this sequence are factors of the final term, $4294967295 = 2^{32} – 1$. Since this is one less than a power of two, it’s a Mersenne number. Why the first $31$ terms are all factors of the 32nd term is difficult to summarise here but there is a thread on StackExchange discussing what happens to the pattern after the $32nd$ term.
$4294967295$ has prime factorisation $3 \times 5 \times 17 \times 257 \times 65537$. These five prime factors are Fermat numbers – numbers of the form $2^{2^{n}}+1$ – in this case with $n = 0, 1, 2, 3$ and $4$. As of the time of writing these are the only known Fermat numbers which are also prime.
These patterns in the rows of the triangle are intriguing, and my own efforts to understand them have uncovered a few other interesting discoveries – notably, that while the 32nd term is not divisible by the 33rd, the 34th term is exactly 3 times the 33rd. The pairs of terms after that seem to alternate, as they do from the start of the sequence, between a non-integer ratio and a ratio of exactly 3, which I conjecture is a pattern that will continue.
Two welcome appearances
$e$ and $\pi$ are two of the most used transcendental numbers. The Swiss mathematician Leonhard Euler (1707-1783) connected them with the most beautiful equation, called Euler’s identity:
\[e^{i\pi}+1=0\]
There are many approximations connecting $e$, $\pi$ and other irrational numbers to be found here.
In 2012 Harlan J. Brothers proved that
\[\displaystyle\lim_{n\to \infty} \frac{\ \displaystyle\frac{s_{n+1}}{s_n}\ }{\displaystyle\frac{s_n}{s_{n-1}}}=e\]
where $s_n$ is the product of the numbers on row $n$ of Pascal’s triangle. The proof can be found on Cut the Knot, part of the wonderful website of Dr Ron Knott.
In 2007 Jonas Castillo Toloza discovered a connection between $\pi$ and the reciprocals of the triangular numbers (which can be found on one of the diagonals of Pascal’s triangle) by proving
\[\pi= 2 + \frac{1}{1} + \frac{1}{3} – \frac{1}{6} – \frac{1}{10} + \frac{1}{15} + \frac{1}{21} – \frac{1}{28} – \frac{1}{36} + \frac{1}{45} + \frac{1}{55} – \ldots\]
Three proofs are given on Cut the Knot.
Harmony in the triangle
The infinite sum of the reciprocals of the Natural numbers is called the harmonic series, $H_n$, where
$H_n = \frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8} \ldots$
The series is divergent, but it crawls its way towards infinity, and takes $15092688622113788323693563264538101449859497$ terms just to pass a total of $100$.
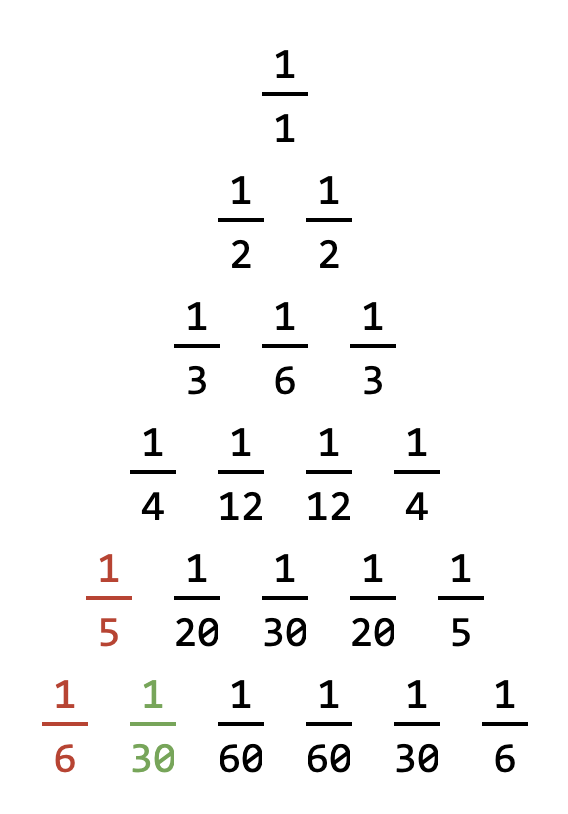
The harmonic series can be used to create a version of Pascal’s triangle – the series itself is placed along the two leading diagonals, and the entries are then related by each being the difference of the fraction to its left, and the one diagonally above it and to its left. For example, $\frac{1}{30} = \frac{1}{5}-\frac{1}{6}$.
Dividing the first term in the $n^{th}$ row by every other term in that row creates the $n^{th}$ row of Pascal’s triangle. The table below shows the calculations for the $5^{th}$ row:
| $\frac{1}{5}$ | $\frac{1}{20}$ | $\frac{1}{30}$ | $\frac{1}{20}$ | $\frac{1}{5}$ |
| $\frac{1}{5}\div \frac{1}{5} =1$ | $\frac{1}{5}\div \frac{1}{20} =4$ | $\frac{1}{5}\div \frac{1}{30} =6$ | $\frac{1}{5}\div \frac{1}{20} =4$ | $\frac{1}{5}\div \frac{1}{5} =1$ |
In our next post, we’ll talk about probability and statistics in Pascal’s triangle, and consider some of Pascal’s other contributions.