I have a new toy. ‘Ox Blocks’ box promises “Noughts and Crosses with a novel twist”.
I heard about Ox Blocks by following along with Maths Jam night remotely via the Twitter hashtag #MathsJam. Alison Kiddle (@ajk_44) tweeted that the Cambridge Maths Jam had been playing back in March.
The game is played as follows. One player plays as ‘O’ (noughts) and the other ‘X’ (crosses). Each turn, a player rolls a cube, or block, which has two faces marked ‘O’, two ‘X’ and two blank. Rolling a ‘O’ or a ‘X’, the player must place the block on the board. Clearly if the roll is in favour of the opponent it must be placed in a way that isn’t useful, if possible. Rolling a blank means the player must remove a block from the board. Play continues with the usual rule of three in a row winning the game.
Standard Noughts and Crosses (or Tic Tac Toe) is a solved game. As described by Alison’s NRICH, this means “if you play correctly you never lose and if your opponent plays correctly you cannot win”. So the introduction of a probabilistic element has the potential to make an uninteresting game slightly interesting.
My first thought was that it must be possible to play with pencil, paper and a normal die. Then I saw that the blanks are not just blank faces, but are hollow, and so supposed that the uneven weight distribution would affect the odds. Specifically, I imagined that the hollow sides would be less likely to roll to the bottom (and therefore the top), thus reducing the odds of a game going on forever. Thankfully, Ox Blocks is readily available via a popular auction site, and I was able to pick up a 1970 copy for £3.80 including delivery.
I took Ox Blocks to the Nottingham Trent University Maths Arcade. This is a lunchtime meeting themed around strategy games for students and staff, well explained elsewhere. Following the example of Noel-Ann Bradshaw at Greenwich, I set up a Maths Arcade at Nottingham Trent after applying for a grant from the IMA with student Kingsley Webster (look out for a piece in the next issue of Mathematics Today!). We have met six times in six weeks towards the end of this academic year to play a variety of games. Most of the games are pure strategy, for good reason, but I thought a bit of probability might be fun one week.
Anyway, my thoughts returned to what the odds are of being able to remove a block. So, in an attempt to settle it, I rolled one block 501 times. The results were as follows:
- ‘O’s: 161
- ‘X’s: 159
- blanks: 181
Surprisingly, this seems fairly even. Let’s make that a little more rigorous. Since I am interested in whether the block comes up blank or not, I can use a two-tailed binomial test with a null hypothesis that the block is a fair die. R gave me the following:
> binom.test(181,501,1/3,alternative="two.sided")
Exact binomial test
data: 181 and 501
number of successes = 181, number of trials = 501, p-value = 0.1848
alternative hypothesis: true probability of success is not equal to 0.3333333
95 percent confidence interval:
0.3191425 0.4050602
sample estimates:
probability of success
0.3612774
This tests whether 181 blanks from 501 rolls is consistent with the probability of a blank being $\frac{1}{3}$. As the p-value is a giant $0.1848$, we don’t have evidence from my block rolling to reject the null hypothesis that blanks come up one third of the time. So, according to my experiment, there’s no reason not to play home grown Ox Blocks with pencil, paper and a normal die.
Of course, this doesn’t quite tell me that the blocks roll perfectly evenly, or if they do it doesn’t explain why the uneven shape doesn’t affect the roll. I suppose the unevenness might be so slight as to not matter, but then why not just make standard dice with blank faces? Any thoughts on the mechanics of the situation would be welcome.


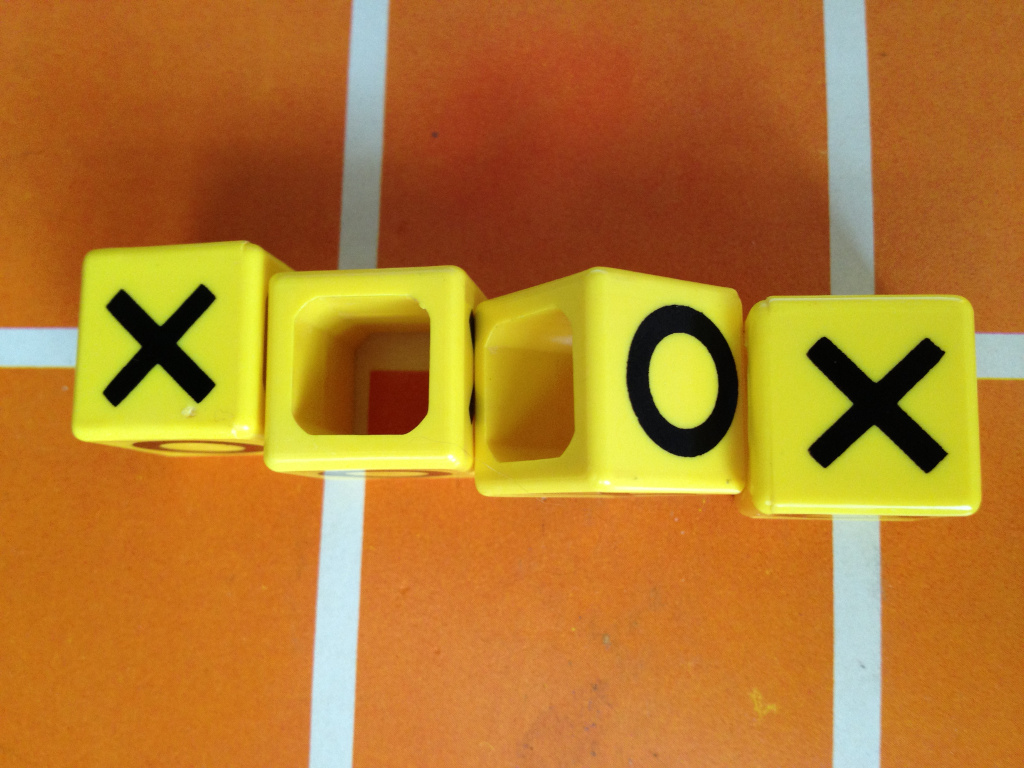
Fast thinking gut hunch is that the centre of mass/gravity is unchanged by the open sides. If one blank side was filled then the centre of gravity would be ‘shifted’ and therefore give a bias.
but then why not just make standard dice with blank faces?
Easy to produce as an extruded item, but also has the advantage of using less material to save on costs.
Paul: I agree, on all points! The symmetry/centre of gravity argument makes some sense, but then why not make solid faces? Some thoughts: I suppose maybe they look cool; maybe they encourage people like me to buy the game rather than using a standard die, thinking there might be a difference; maybe the manufacturers thought there might be a difference; maybe there is a difference, but a small one; maybe they are designed to show off a plastic manufacturing technique (the game is made by Vic-Toy, “A Division of Invicta Plastics Ltd.”).
I’m so pleased that my tweet about Ox Blocks generated some interest! I’ve been playing around with probability simulations to support the activities on http://nrich.maths.org/probability, so perhaps I ought to take the time to write an online version of Ox Blocks…
Alison: if you were pleased to pique my interest, try this one:
Depends how you roll it. If you roll such that the hole stays horizontal then blank will never come up. If you roll such that the hole goes end over end then blank will come up from time to time. Did you carefully randomise these orientations?!!!
You can bias a regular die the same way. To work, any die has to bounce around enough to approach its equilibrium distribution.
Making one moment of inertia different than the other two makes the probability of rolling from “axis vertical” to “axis horizontal” different than “horizontal-horizontal”, but the probability of each transition is still the same as its reverse. The equilibrium probabilities are still uniform.
Also, note that the moments of inertia are not *much* different. The maximum ratio (achieved by a thin walled tube) is only 1.2.
The purpose of the holes is clearly to start discussions on blogs, and get free advertizing :-)
My copy is marked 1970, which I believe is a little pre-blogs, but not pre-discussion or advertising! I expect it might be an attempt to convince people they need to buy a copy, rather than being able to use any old dice.
I agree with Ralph about the bias. I did throw each roll from a decent height so it bounced around a lot. Is there a proper methodology for testing dice?
Still, good science is reproducible, and I’d be pleased to hear from anyone attempting to replicate my results!
My original comment was intended as tongue-in-cheek. However, on reflection I think there might well be a bias in the way one holds these dice. A normal die feels essentially the same whichever way you hold it; but one might have a tendency to hold a die that has a big hole through it in a preferred orientation. I don’t know, I haven’t got one! However, as long as it bounces around a lot I guess this shouldn’t matter!
Coincidentally, I recently made an Android App ChaoTic-Tac-Toe that plays like this “Ox Blocks” game does.
You can customize the probability of “rolling” an X, an O, or a bomb (the remove action in my version). By default, the “Chaotic” version sounds just like “Ox Blocks” with the equal probabilities. An interesting thing is that twiddling with the probabilities allows three main types of games: traditional (100% chance of “your” marker), reverse (100% probability of your opponents marker), and chaotic. And if you find that the chances of the actual physical dice are not equal, you can create a custom game to twiddle the percentages.
The game supports realtime online multiplayer, for those that want to play family and friends not nearby!
(Sorry it is rather low-end graphics– I focused more on functionality, and need to learn more about Android graphics to make it prettier.)
Hi Rob, sounds good. Reverse [Noughts and Crosses] sounds interesting.
You say “coincidentally”, so I was wondering where you got the idea from? Did you see something similar somewhere else, or come up with it independently?
Hi Peter,
Thanks for the interest. The reverse style definitely takes some getting used to- my son would have more chance to beat me in that style due to my “blindness” of not seeing the “right” (wrong?) move to make.
I may have seen a reference to OxBlocks I think through BoingBoing.net a few years ago. The “coincidentally” was just that I found your discussion after I published my game.
Rob