Friend of the site and good writer/bad drawer Ben Orlin has recently released a new book, and we were kindly sent a copy to play with and review.

The full title is “Math Games with Bad Drawings: 75¼ simple, challenging, go-anywhere games – and why they matter”, and it’s a sizeable collection of fun pen-and-paper games you can very much play anywhere, along with some enjoyable discussion of the logic, strategy and maths behind them (accompanied by the usual hilarious, beautifully-pitched bad drawings to bring it to life).

Following on from Ben’s two previous books Math with Bad Drawings (2018) and Change is the Only Constant (2019), this book is the product of a few years of careful research, clever design and extensive play-testing – some of which was outsourced to a large collection of internet friends and followers – and the result is worth the wait. It’s a hefty tome – bigger than you’d expect it to be – and full from cover to cover.

The subtitle promises $75 \frac{1}{4}$ games, and they’re divided into five chapters. Starting with spatial games like noughts and crosses (obviously, the book doesn’t cover boring games like plain noughts and crosses – but goes into depth on some fun variations), then moving on to number games, logic games, probabilistic games (‘of risk and reward’) and information-based games. It’s a sensible taxonomy, and allows for some nice parallels to be drawn between similar ideas.

The book also does a great job of including some lovely mathematical explanation – sometimes not even directly related to the game being discussed. For example, a game of meta-noughts-and-crosses, where each of the nine cells in the grid itself contains a smaller game of noughts and crosses, is a good excuse for a sidebar about fractals and self-similar structures.

The games themselves are well-chosen and generally well explained – we got together a few mathematicians to play through some of them, and found the games wonderfully easy to understand and play, but almost immediately became engaged with much deeper questions about strategy and the consequences of our decisions. It wasn’t quite as bad as this old SpikedMath comic but we spent a lot longer thinking about our moves than we needed to, and thoroughly enjoyed it.

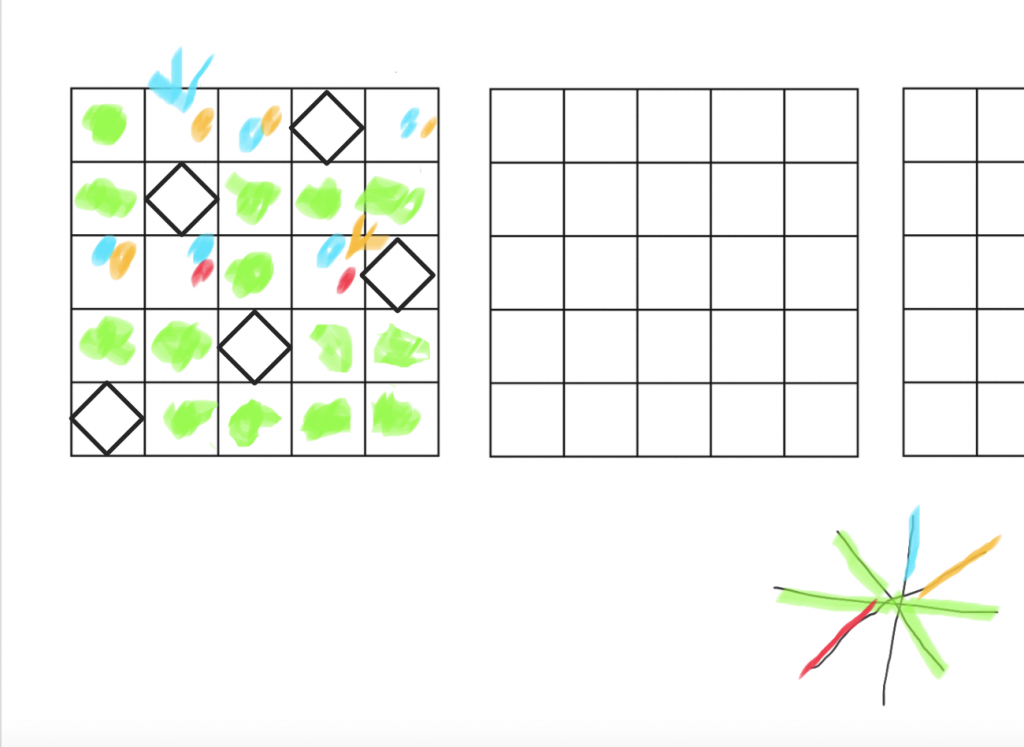
We got particularly into a game called Dandelions, which was an asymmetric game involving one player placing dandelion ‘seed heads’ into the cells of a grid, with the other then deciding which way to blow the wind, which would spread the seeds across the grid in the direction the wind is blowing. The challenge is for the player who’s Dandelions to cover the whole grid, and the player who’s The Wind trying to choose which direction to blow in each turn so that the whole grid doesn’t get covered in dandelion seeds.

A game of Ben’s own designing, a little discussion and clarification was sufficient for everyone to understand the rules, and like all the games in the book, it was simple to play. Since we were playing over a video call, we used Google Jamboard as a virtual piece of paper, and were able to paste in an image of a 5 by 5 grid, drop in shapes and scribble with the coloured pens. (Other online whiteboards are available).

Our game above shown in green, and was abandoned at the point it was clear who was going to win. At that point, we erased the last couple of moves and worked backwards to pinpoint the exact moment when I lost, and see whether other moves earlier could have prevented it. The different colours show which squares would have been covered if the wind had chosen to blow in that direction.

After some discussion, we concluded that playing as dandelions gave a massive advantage, and it was very difficult for the wind to prevent the whole grid being filled – but maybe a bigger grid would make it more balanced.

Luckily, as well as the basic rules of each game, the book includes suggestions for these kinds of variations on the original rules, as well as discussion of how these versions might differ, and who would benefit in each case. This one also included a symmetric variant (in which the ‘wind’ is decided by a dice roll) and adaptations to make it easier or harder for each player.

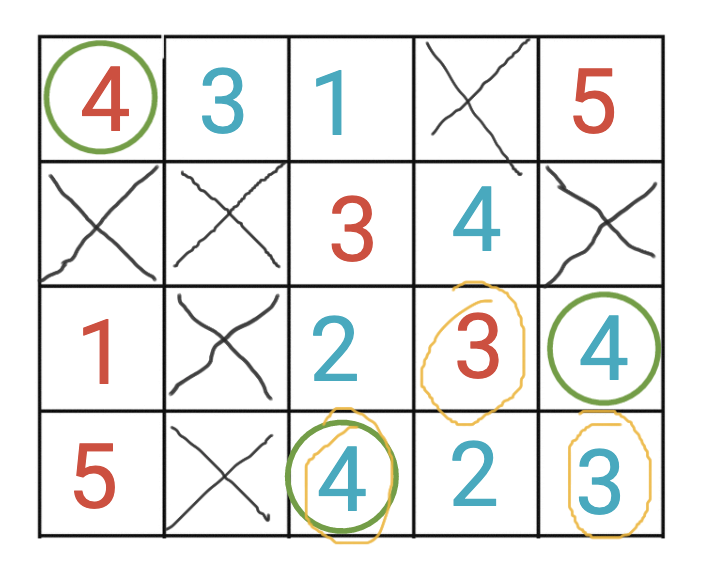
We also had a play with a game from the Number Games chapter called Prophecies, designed by Andy Juell for a game design competition in 2010. The game involves placing the numbers 1-5 (with at most one of each in a row or column), or crosses, in the squares of a grid until the grid is full, at which point any number which accurately predicts how many numbered cells are now in its own row or column will score points for the player who placed it.

Below, you can see the results of one game, with two players using red and blue numbers, and the green round circles indicating numbers that scored in their row, and the yellow scribbled circles showing numbers that scored points in their column (with a 4 at the bottom counting towards both).

We undertook a similarly in-depth analysis of the game – not because we felt we needed to in order to review it, but purely because it led us in that direction. This game has difficult tug-of-war on your priorities, between making good moves for yourself and blocking the other player from scoring (which as I found to my detriment, can fail as a strategy if you do too much of it).

The games are mostly two-player, with a few for three or more players, and some include variants that allow for more to play cooperatively – or you can play a two-player game in teams and really debate every move and get properly into the analysis (or, just take turns choosing a move while playing in silence).

The games are designed and chosen to be simple but lead you to much longer introspection, and it’s a lovely combination. In one short evening we managed to barely scratch the surface of the vast quantity of games in the book, and I anticipate a full read-through might be necessary to find all the hidden jokes, clever twists and fun mathematical ideas it contains.

Math Games With Bad Drawings is released on April 5th (US) and 7th April (UK), and can be found in several good bookstores (US) and several good bookshops (UK). There’s also a boxed version which will be out in October, including wipe-clean boards, pens and instructions for 34 of the games (which I will definitely be getting for literally everybody I know for Christmas).