From Zero to Hero: a Euclidean proof

It used to live, unloved, in the A-level formula book: a mysterious result relating the area of a triangle to its sides. The most interesting thing about it was its name: Heron’s formula. (As far as I can make out, the chap’s name was Hero of Alexandria, and if you do a possessive in Greek it goes into the genitive case, which makes it Heron’s Formula. You might want to debate this; I regretfully decline.)

The Call To Adventure

Love Triangle is available wherever good books etc. are, from June 20th – and signed preorders are available from Maths Gear

So there I was, peacefully proofreading Matt Parker’s forthcoming book Love Triangle when I was shocked by a vicious — and frankly unprovoked — assault on the very idea of Heron’s formula.

Yeah yeah yeah. Let ABC be a triangle with area $ \Delta $, side lengths $ a$, $b$ and $c$, and semiperimeter $s = \frac{a+b+c}{2}$.

It was never my favourite formula, sure, but it occasionally saved a step. And there’s a certain sleekness to it, at least if you square it to get its nicest form: $ \Delta^2 = s(s-a)(s-b)(s-c) $.

Of Matt’s many complaints about our poor first-century-CE friend’s contribution to the literature, one did strike me as valid: there isn’t a nice proof of it. You can make like Hero himself and do some jiggerypokery with a degenerate cyclic quadrilateral, you can follow Sir Isaac Newton’s lead and wrangle the algebra, or you can trigonometry yourself to death.

This surprised me. Surely a nice symmetric formula should have a nice symmetric proof? According to the Wikipedia citations, I’m not the only person to think that. It was also something that interested John Horton Conway — a clue that led me to a lovely proof.

The First Threshold

Once upon a time, back in the heady days when Christian had an occasional few minutes of free time, this esteemed organ ran a Big Math[s]-off. One of my few successful submissions was a proof without words of Conway’s Circle Theorem. It was a very nice proof without words; however, I now have a better and clearer one.

Conway’s Circle Theorem states:

Given triangle ABC, extend sides AB and CB through B by a length equal to side AC. Similarly, extend sides BA and CA and through A and sides AC and BC through C to define the six Conway points. Then the ends of these sides lie on a circle (the Conway Circle) which is concentric with the incircle of ABC.

I mean, what?! I’ve proved this several ways and it still seems absurdly neat.

The simplest proof I have looks like this:

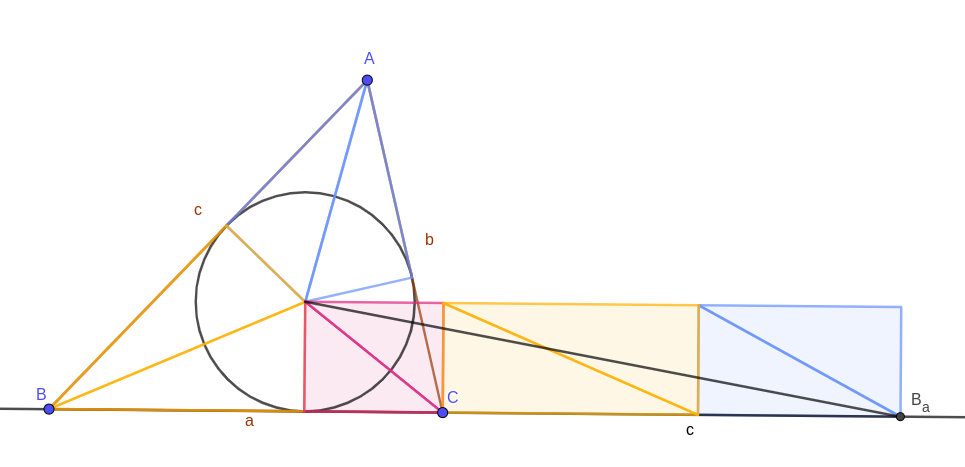
A visual proof of Heron's formula. A triangle ABC is split into six right-angled triangles, the hypotenuse of each of which links a vertex to the incentre.

The six triangles are then rearranged to make a rectangle with a height equal to the inradius and a base equal to the semiperimeter.

The radii of the incircle that reach the edges, and the segments connecting the incentre to the vertices, naturally divide triangle ABC into six triangles in three congruent pairs. These can be rearranged to make a rectangle as shown; the most distant point on the rectangle is a Conway point.

You can do the same thing either way from any of the three inradii, giving you the six Conway points; all of the rectangles are congruent, so their diagonals have the same length. In other words, all six Conway points are the same distance from the incentre, so they lie on a circle that’s concentric with it $ \blacksquare $

That’s tidy and all, but what’s really interesting is that the rectangle shown has the same area as triangle ABC does — it’s made up of the same six triangles. One of the rectangle’s edges is equal to ABC‘s inradius and the other is equal to its semiperimeter. And the only other place I’ve ever seen a semiperimeter mentioned is in Heron’s formula.

Approach to the inmost cave

We’re currently simultaneously close but some way off: we can see that $ \Delta = rs$ — but there’s no immediate sign of $ (s-a) $ and its friends. They’re there if you look closely, though: each of the six triangles has a leg of the right form. For example, the red triangle has one leg of length $ r $ and the other of length $ s-c $.

Unfortunately, multiplying them together is non-trivial and is going to take a little work.

You’ll also see a lot of dry, technical alphabet soup that I’ve tried to avoid here — think of this as a somewhat coherent argument rather than a proof.

Let’s sidetrack for a moment and talk about the difference between finding and presenting a proof. If you look at the “final version” of this proof, currently going through peer review at Mathematics Magazine, you’ll just see a clever sequence of triangle manipulations. You won’t see the dead-ends and mis-steps, of which there were many.

For example, the first time I noticed the semiperimeter thing, I thought “I just need to prove that $ r = \sqrt{\frac{(s-a)(s-b)(s-c)}{s}} $.” I then realised how much heavy lifting that “just” was doing and set it aside until spurred back into action by a Parker diatribe.

I spotted there was another way: if I could show that the base of the rectangle was equal to $ \frac{(s-a)(s-b)(s-c)}{r} $, then I could multiply the two areas together to get $ \Delta^2 $. So that’s what I did.

The battle begins

We’re going to need some letters, I’m afraid.

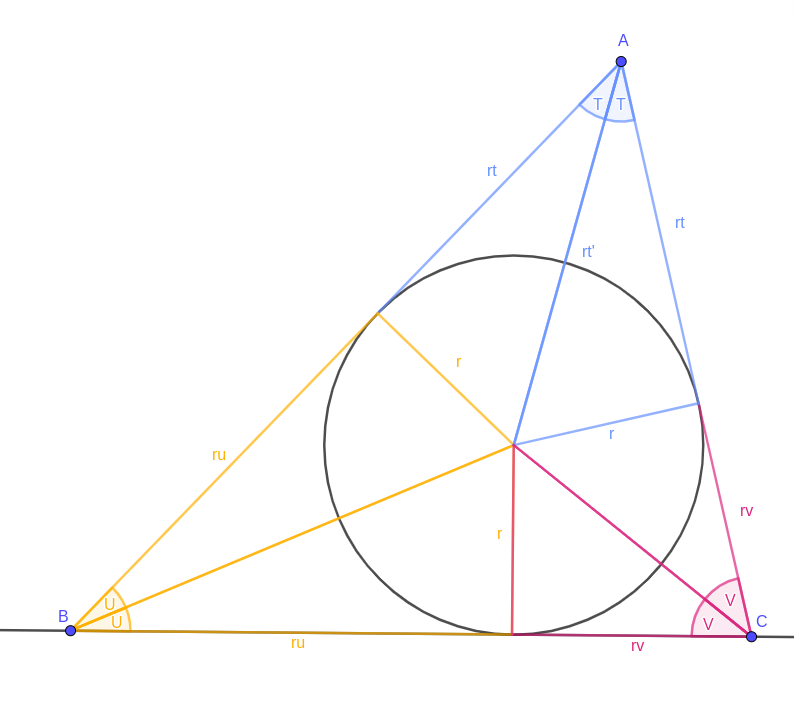
A triangle ABC divided into six right-angled triangles as before.

Two congruent (reflected) triangles in blue share a vertex at A; they have legs of length r and rt, and a hypotenuse of rt'. The angle in each triangle at A is marked T.

Two yellow right-angled triangles share a vertex at B. Their legs are of length r and ru, and the angle of each at B is U.

Two pink right-angled triangles share a vertex at C. Their legs are of length r and rv, and the angle of each at C is V.

This is the same triangle ABC as before, with the same triangles, but it’s helpful to label things. Call the inradius $ r $. The half-angles at A, B and C are $ T $, $ U $ and $ V $ (respectively), and the segments linking each to the incircle have lengths $ rt $, $ ru $ and $ rv $ — it makes the algebra simpler later to keep a factor of $ r $ in there. Lastly, the segment linking A to the incentre has length $ rt’ $.

The main idea of this proof is that you can multiply lengths together by scaling triangles.

Triangle 1

Start by building a triangle similar to a blue triangle (the ones containing point A) and match its “$ r $” leg to the “$ rv $” leg of a pink triangle (containing C).

This scales the blue triangle by a factor of $ v $, so the new blue triangle’s other leg has length $ rtv $. Its hypotenuse has length $ rt’v $, but we won’t need that until later on.

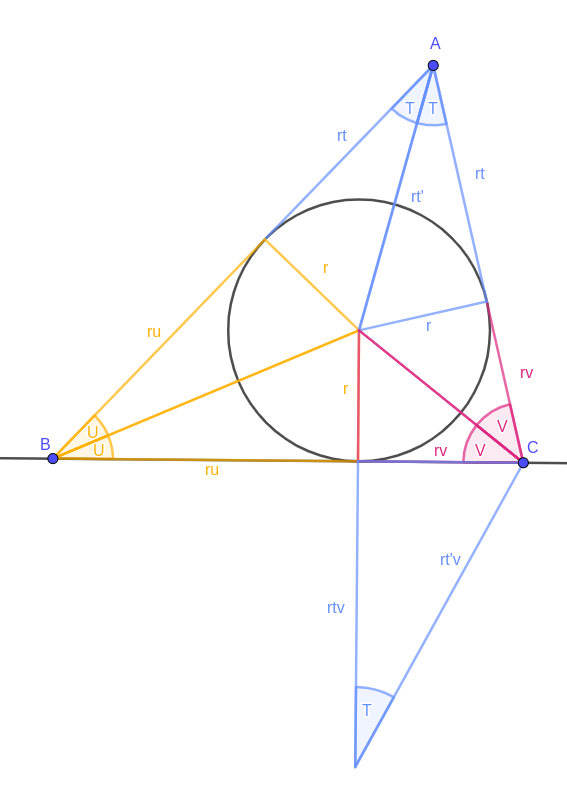
A triangle similar to the blue triangles is constructed, scaled so its "r" side coincides with one of the "rv" sides of a pink triangle. Its other leg is maked rtv, and the hypotenuse rt'v.

Triangle 2

Now I’m going to scale a yellow triangle (containing B) so its “$ r $” leg matches the “$rtv$” leg of the new blue triangle. Because it’s scaled by a factor of $ tv $, its other leg has length $ rtuv $.

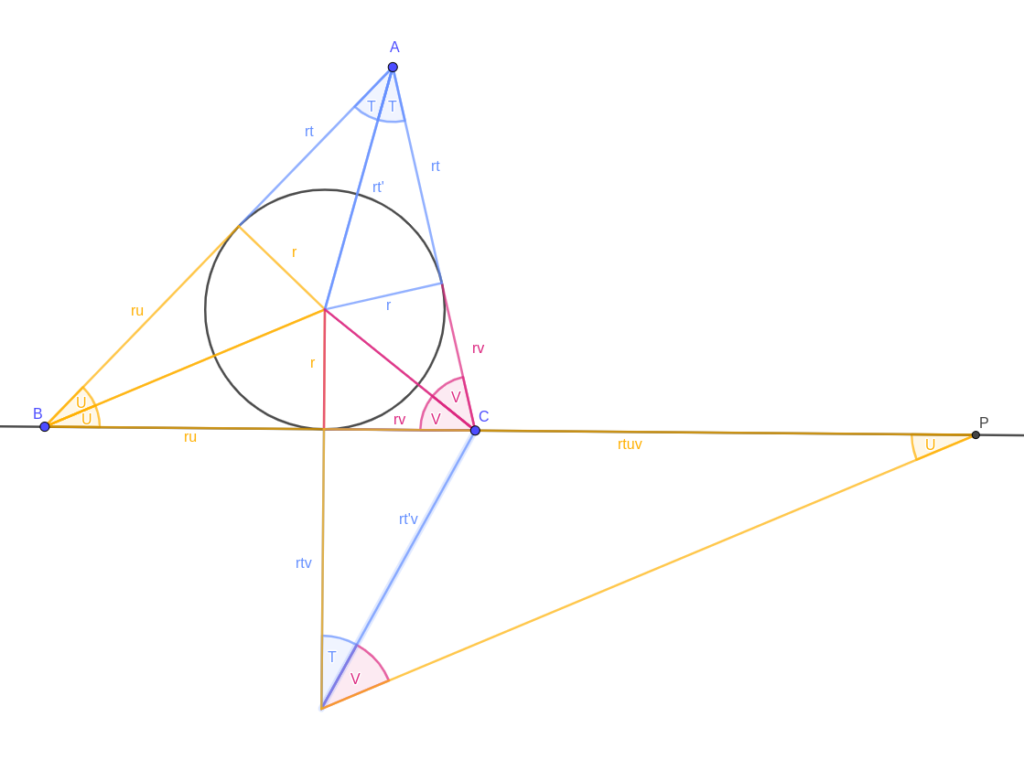
A triangle similar to the yellow triangles is added, scaled so its "r" side corresponds to the "rtv" side of the new blue triangle. The other leg has length rtuv, and the apex is marked P.

The angle between the blue and yellow hypotenuses is marked V.

A couple of claims here: firstly and easily, the angle between the blue and yellow hypotenuses is $ V $ — this must be the case because $ 2T + 2U + 2V = \pi $ and the non-right-angles of our yellow monster add up to $ \frac{\pi}{2} $. Secondly, I claim that the apex of the yellow triangle (marked P) is a Conway point. That takes a bit more justification, and two more triangles.

Triangles 3 and 4

If I drop a perpendicular to the blue hypotenuse at C, I get a triangle that’s similar to the pink triangle. Its scale factor is $ \frac{t’}{v} $, and the new leg has length $ rt’ $.

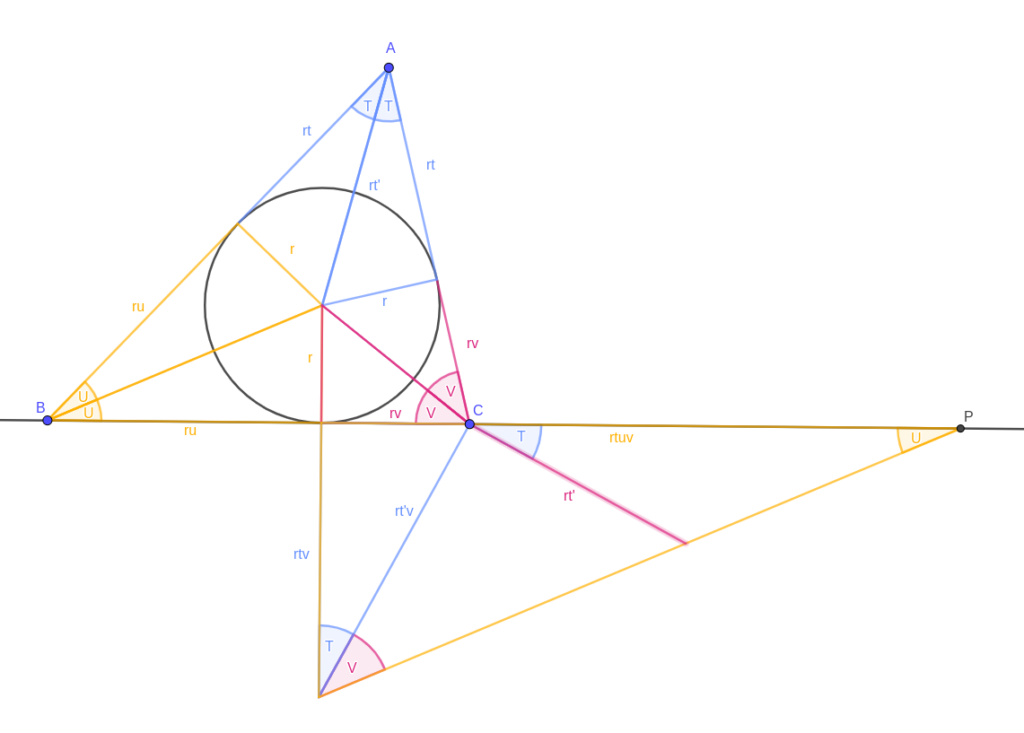
A line segment is drawn in pink perpendicular to the blue hypotenuse at C, meeting the yellow hypotenuse. Its length is rt', and the angle between it and the segment CP is marked T.

What about the other triangle, with CP as an edge? That has the same angles as the triangle connecting A and B with the incentre — and it has a pair of corresponding sides the same length, so the two are congruent. In particular, it means that CP has length $ rt + ru = c $. A point on BC extended, a distance of $ c $ away? That’s a Conway point.

Slaying the beast

The rectangle from Conway’s Circle Theorem earlier had area $ rs $, so we can write $ \Delta = r^2(t+u+v) $

But we also just worked out that the yellow triangle’s leg — which corresponds to the “$ s $” edge of the rectangle — has length $ rtuv $, so we can write the rectangle area as $ \Delta = r^2 tuv $.

Multiplying the two $ \Delta $ equations together gives something I’m going to arrange as $ \Delta^2 = r(t+u+v)(rt)(ru)(rv) $.

Meanwhile, you can remember from earlier that $ rt = s-a $, $ ru = s-b $ and $ rv = s-c $ and out jumps $ \Delta^2 = s(s-a)(s-b)(s-c) $, which is Heron’s formula $ \blacksquare $

Triumphant return

Just because I wondered and looked it up: Euclid flourished about as long before Hero did as Newton did before me. Assuming that writing for the Aperiodical is what counts as flourishing.

Doris Schattschneider — who didn’t exactly coerce me into writing this up as a proper paper, but from certain people the phrase “I do hope…” has as much weight as a command — tells me she isn’t aware of a previous proof of Heron’s formula that only uses synthetic geometry. I don’t really know what that means, but I gather it’s something to do with what Euclid could have done.

I find it a little hard to believe that nobody in the last couple of millennia has stumbled on something akin to this, but in any case, my approach to figuring things out is similar to the fabulous Moose Allain‘s approach to jokes (I paraphrase, and I speak only for me): it doesn’t matter if someone else thought of it first, you’re still allowed to take joy from thinking it up yourself, and you’re still allowed to share it.

This proof brought me great joy. And maybe it’ll help Matt see another side of Heron’s formula.

One Response to “From Zero to Hero: a Euclidean proof”

CJ June 18th, 2024

The main synthetic proof of Heron’s I know of uses the incenter-excenter lemma. Construct the $A$-excenter $I_A$, and let $r_A$ be the $A$-exradius. From similarity with the right triangles with hypotenuses $AI$ and $AI_A$, we get
\[ \frac{r}{r_A} = \frac{s – a}{s}. \]

Another similarity is with the right triangles with hypotenuses $CI$ and $CI_A$. (The reader can check this by proving $\angle ICI_A = 90^{\circ}$.) From this we get
\[ \frac{r}{s – c} = \frac{s – b}{r_A}. \]

From the first equation we get $\Delta = rs = r_a(s – a)$, and by substituting $r_a$ from the second equation, we get
\[ \Delta = \left( \frac{(s-b)(s-c)}{r} \right) (s-a). \]
Multiply this by $\Delta = rs$ and taking the square root gives Heron’s.

The Aperiodical

You're reading: Irregulars