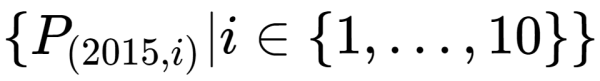Before Christmas, we launched a winter-themed maths competition – to design a sensible hexagonal snowflake, using a square grid, which could be used to knit a wintery jumper and not a) look terrible or b) have non-hexagonal symmetry. We had a deluge of entries, some valid and others less so – in fact, we may have had at least one entry break each of the rules we set. Below is a round-up of all the entries we received.
You're reading: Main
New Mersenne prime discovered, and promptly printed out
Breaking news! On 19th January 2016, the Great Internet Mersenne Prime Search discovered a new largest prime number – we know 49 Mersenne primes, the largest of which is now $2^{74207281}-1$, a number containing over 22 million digits and full of primey goodness.
Internet Maths Person Matt Parker has responded to the news in spectacular style, by issuing a 14-minute long video explaining the discovery and its implications, as well as somehow scoring an interview with the actual discoverer of the new prime, Curtis Cooper.
Our top 10 posts from 2015
In 2015 The Aperiodical went from strength to strength again, with 179 posts published by 18 authors. I’ve collected our ten most popular posts from 2015, in case you missed them.
Relatively Prime Recap: Season 2, Episode 3: Mathematistan
I have to say, I chuckled: the week Relatively Prime hits ‘noteworthy’ on iTunes is the week Samuel discusses using maths to do well in popularity contests. Coincidence? I think not.
To me, episode 3 of the second series represents something of a return to form for one of the top half-dozen maths podcasts around; whether this is because I’m a fan of political maths or because it’s genuinely really good is a) difficult to tell because I’m biased and b) a false dichotomy.
Books a 14-year-old who’s good at maths might enjoy
My good friend David Cushing popped on Facebook messenger to ask me a question:
I did tweet it, and I got a lot of good responses. Before I tell you about those, I’ll quickly list the books we mentioned above, that of course a keen 13-year-old already has.
Relatively Prime Recap: Season 2, Episode 2: Your Daily Recommended Math[s]
Maths – as teachers are fond of telling anyone who’ll listen – is everywhere. In this difficult second episode of the difficult second series of Relatively Prime, Samuel Hansen shows us a few important places where it can be a help: at the petrol pump, at the birthday party, in the car park and at the bar — or rather, in deciding whether to go.
MathsBombe Competition
From the team that brought you the Alan Turing Cryptography competition, Manchester Uni’s maths department are running another schools maths puzzle competition, this time called MathsBombe.
Aimed at students up to Year 13 (England and Wales), S6 (Scotland), Year 14 (Northern Ireland), the competition starts on 13th January, and teams of up to 4 can register.
The puzzles will be released every two weeks, in four sets, and there’s a prize for the team solving each puzzle set first. There are plenty of other prizes too, and it’s free to enter. There’s still time!
More information: MathsBombe website.