In my capacity as someone who occasionally turns up and does maths at people, I often find myself exposed to ‘starter puzzles’ – things the organisers provide to whichever group of humans have come to see me do maths, to give them something to do in any waiting time before the event starts. This is, of course, a fantastic source of ideas for the MathsJam I run in Manchester, as well as just being great for me as I get to have a go at them all.
You're reading: Posts Tagged: puzzle
On Disreputable Numbers
One would be hard put to find a set of whole numbers with a more fascinating history and more elegant properties surrounded by greater depths of mystery — and more totally useless — than the perfect numbers.
— Martin Gardner
There are countless ways to classify integers. Happy, perfect, friendly, sociable, abundant, extravagant, cute, interesting, frugal, deficient, hungry, undulating, weird, vampire… the list goes on. But how useful are such classifications, beyond their inherent interestingness, and as a hook to get people into number theory?
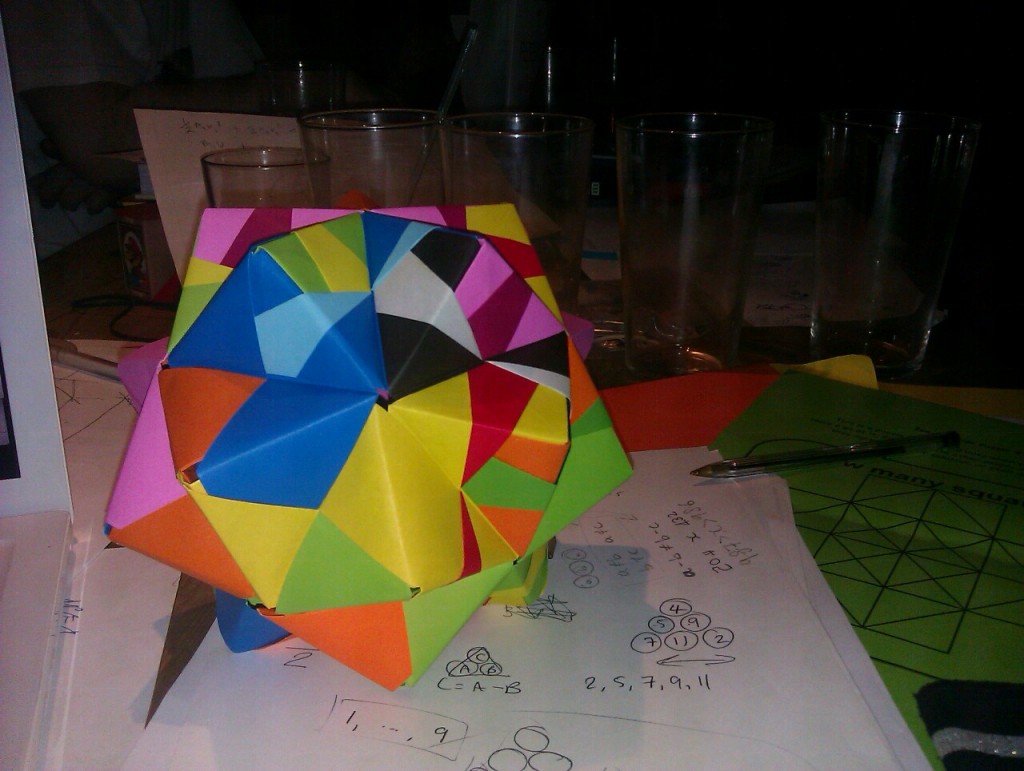
Manchester MathsJam March 2012 Recap
This month’s MathsJam was well attended – we matched last month’s turnout of 11, albeit one of that number was in the form of Ed Bradshaw, the organiser of the Washington DC MathsJam. For Ed, it was 4pm and he was in his office, using Google Plus for a live video connection to a MathsJam halfway around the world. The video connection worked fine, although in a noisy pub we struggled to hear what Ed was saying on my laptop’s tiny speakers, so for some of the evening we used headphones and took it in turns to be in conversation with Ed.
Puzzlebomb – March 2012
Puzzlebomb is a monthly puzzle compendium. Issue 3 of Puzzlebomb, for March 2012, can be found here:
Puzzlebomb – Issue 3 – March 2012
The solutions to Issue 3 can be found here:
Puzzlebomb – Issue 3 – March 2012 – Solutions
Previous issues of Puzzlebomb, and their solutions, can be found here.
Another black and white hats puzzle
A classic maths puzzle involves a line of one hundred prisoners, who have each been given a black or white hat by their nefarious captor, and must each correctly shout out the colour of their hat to win freedom. The twist is that the prisoners don’t know the colour of their own hat, and though they can see the colours of the hats in front of them, they don’t know many of each colour there are overall. They can confer on a strategy beforehand, and the aim is to get as many of them to correctly identify their hat colour as possible. You can find a full explanation here (and in many other places!)
There are several ‘sequels’ to this puzzle, some involving an infinite number of prisoners and requiring the axiom of choice to solve. This post is about a nice variation on the theme that I heard about at a recent MathsJam. It can (just about) be solved without knowledge of higher mathematics, and though it seems impossible at first glance, the prisoners in this situation can in fact save themselves with 100% certainty.
Using a zero-knowledge protocol to prove you can solve a sudoku
I’ve just uploaded to youtube a video I made with Katie Steckles to demonstrate why zero-knowledge protocols exist and how one works.
Katie is a habitual liar, so we followed the zero-knowledge protocol described in the paper, “Cryptographic and Physical Zero-Knowledge Proof Systems for Solutions of Sudoku Puzzles” which you can download from http://www.mit.edu/~rothblum/papers/sudoku.pdf
By following this protocol, Katie can prove that she isn’t lying to me about being able to solve the puzzle, without revealing anything about how she solved it.
The paper I mentioned, “How to explain zero-knowledge protocols to your children” is an excellent explanation of the ideas behind zero-knowledge proof.
MathsJam Manchester, February 2012
This is a roundup of things which happened at Manchester MathsJam, February 2012.
First, we discuss a puzzle I found on Futility Closet, a blog of curiosities by Greg Ross which is sometimes mathematical. The Martian Census Bureau compiled the marital history of every male and female Martian, living and dead: Never married: 6,823,041; Married once: 7,354,016; Married twice: 1,600,897; Married three times: 171,013; Married four times: 2,682. What’s wrong with these figures?