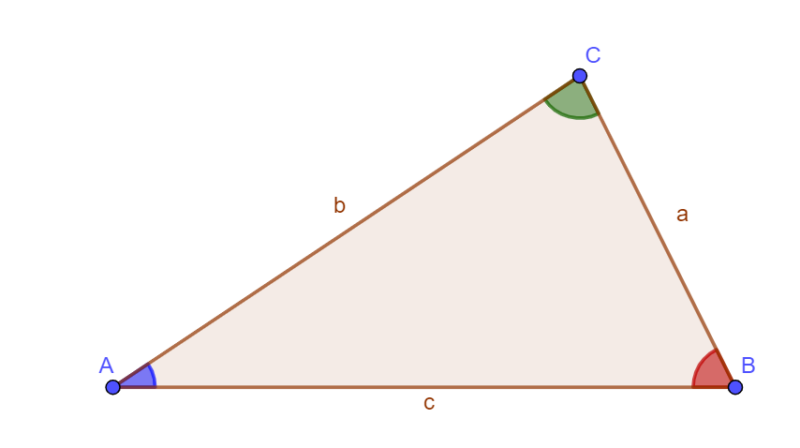
This is a guest post by Elliott Baxby, a maths undergraduate student who wants to share an appreciation of geometrical proofs. I remember the days well when I first learnt about loci and constructions – what a wonderful thing. Granted, I love doing them now; to be able to appreciate how Euclid developed his incredible…