
Actual aperiodicity news on The Aperiodical!
This is probably the biggest aperiodicity news we’ll ever cover here: David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss have produced a single shape which tiles the plane, and can’t be arranged to have translational symmetry.
And it’s so simple!
Geometers have been looking for a shape with these properties for over 60 years, and until this example was found it wasn’t clear that one would exist at all.
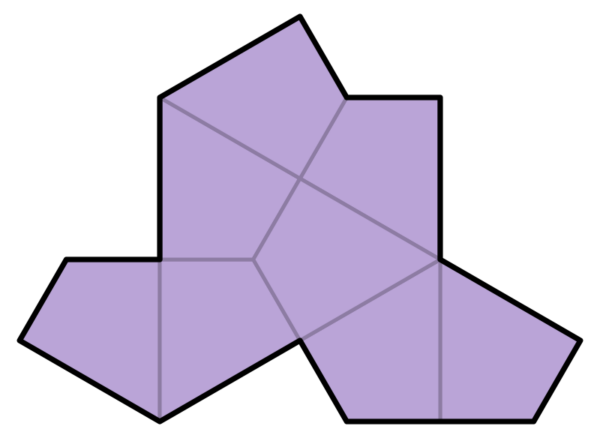
The tile is made of eight kites – the shape you get by cutting a hexagon up through the midpoints of its edges.
In fact, they show that there’s a whole continuous family of aperiodic monotiles, obtained by changing the lengths of the edges in the shape shown above. Here’s an animation by Craig Kaplan showing a continuous transformation through the whole family:
Note that there are three points in the animation where the shape is degenerate (at the start, middle and end) because two adjacent edges become parallel, and those shapes can tile periodically.
The authors have put together a website to accompany their paper proving the shape is an aperiodic monotile. Have a go at reading the paper: it’s really well written, and starts with a detailed introduction describing the problem and its history.
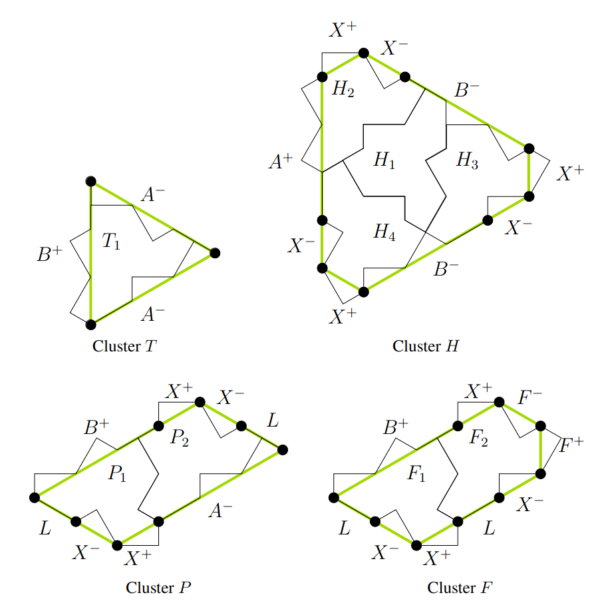
There’s also an interactive tool for producing patches of the tiling. It wasn’t immediately clear to me how it works: you pick which of the basic clusters H, T, P or F you want to start with, and then click “Build supertiles” to apply the substitution process and end up with a bigger patch of tiles.
It’s worth noting that this is just a preprint, so a mistake in the proof might be found, but this announcement is credible: the authors are well-known geometers who have been working on this and similar problems for a long time, and the outline of the proof looks coherent.
The authors call their shape the “einstein hat”, punning on the German “ein” – one, “stein” – stone (or tile). It’s fairly safe to predict that if the “einstein” part sticks, future generations will be confused about whether Albert Einstein was involved. Opinion differs on whether the shape looks more like a hat or a t-shirt.
David Smith has published a ‘scrapbook’ on his blog giving some of the story of how the shapes were conceived. David notes that they actually discovered two monotiles: the ‘hat’ (or t-shirt) above, and a shape made of 10 kites that looks like a turtle:
An explanation of what it’s all about that you can handwave your way through at the dinner table
Think about the 2D plane – an infinite, flat surface. How can you completely cover it up? If you’ve got an infinite supply of tiles, can you arrange them together on the plane so that there are no gaps?
If the tiles can be any shape you like, you can put them down however you like and then fill in any gaps with just the right shape. So it’s more interesting to restrict yourself to a certain, finite, set of different tile shapes.
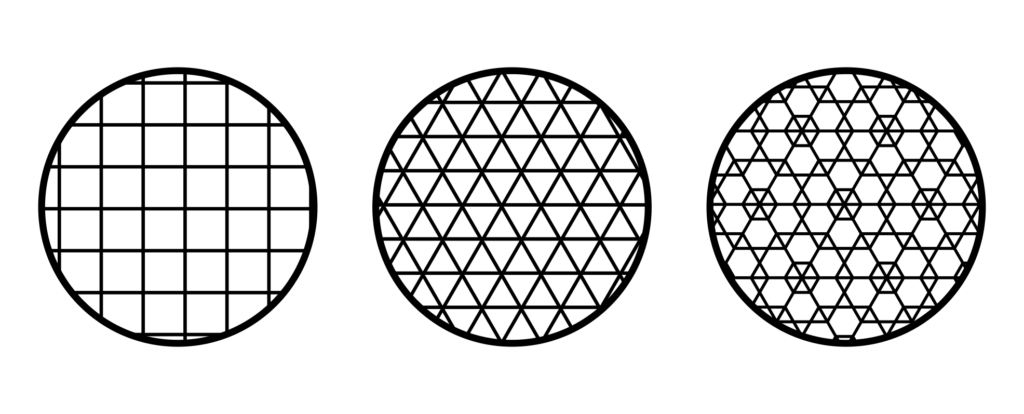
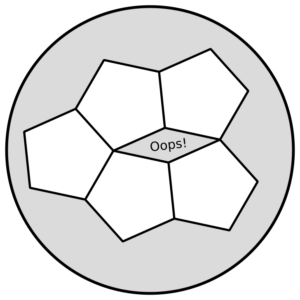
You can do this with infinitely many squares of the same size, or with a mix of equilateral triangles and regular hexagons. If all you’ve got is regular pentagons, you can’t do it: no matter how you arrange them, eventually you’ll end up with a gap that’s too small to put a pentagon tile in.
The next question is: once you’ve put the tiles down, are there any symmetries? If you just used squares, then you can move every tile one space down and it’ll look exactly the same as it did before.
Is it possible to arrange the tiles so that there’s no translation symmetry – so that each point in the plane looks completely unique? This is called a non-periodic tiling.
If you split up a square into a few rectangles with the same proportions, you can produce a non-periodic tiling of the plane by arranging them in a different configuration depending on their position on the plane. But you could also arrange them the same way everywhere, so there would be translation symmetry.
The interesting question is: are there any tiles, or sets of tiles, that can cover the plane, but never with translation symmetry – a truly aperiodic tiling?
The answer is yes: most famously, Roger Penrose found a pair of shapes – a kite and a dart, with specific edge lengths, or alternately a pair of rhombi, marked so that they obey certain edge-matching rules – that together tile the plane, but can never produce translation symmetry. Versions of the shapes which encode the matching rules, with chunks removed and added from the correct edges to force the matching (like the ones shared by Edmund Harriss in our Math-Off) constitute true aperiodic tile sets.

It’s also possible to tile the plane non-periodically using a single tile, called a monotile – for example, the pinwheel tiling consists entirely of copies of a right-angled triangle with sides of length $1$, $2$ and $\sqrt{5}$ – but this shape could also form a periodic tiling, and in order to force the tiling to be aperiodic, matching rules are needed.
What nobody knew until now was whether there’s a single tile shape that generates only aperiodic tilings, without needing to specify matching rules – an aperiodic monotile.
That’s what Smith, Myers, Kaplan and Goodman-Strauss have found. They’ve proved that it tiles the plane, which is the easy part, and then proved that it must tile aperiodically. They came up with a new technique for proving this – actually, two: they proved it twice, just to be sure.
That’s the short version of the story. If your dinner companions are still interested, here’s some more explanation of how the aperiodicity proof works. Maybe pause for a bit, make sure your dinner isn’t getting too cold, and do some finger exercises to prepare for all the handwaving you’re about to do.
The authors show that no matter how you put the tiles down, it will always be possible to divide it up so that each tile belongs to one of a set of four clusters – specific arrangements of 1, 2 or 4 tiles – and that the edges on adjacent clusters can only match up in certain ways.
This part of the proof is done with computer assistance: there are lots of cases, and it’s likely you’d make a mistake while trying to draw them out on paper, so instead the authors rely on verifying that the code for their checking program is correct.
They then show that these clusters can themselves always be separated into larger groups called metatiles, which have the same symmetries as the basic tiles. So if the tiling when looked at as a collection of single tiles has translational symmetry, then looking at it as a collection of metatiles must also have that symmetry.
And then they show that the metatile tiling can’t have translational symmetry! So the monotile tiling doesn’t either!
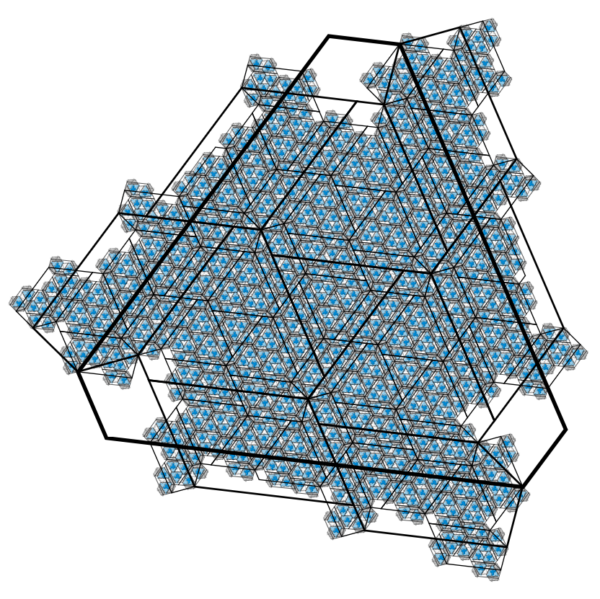
To show that the metatile tiling is aperiodic, they just do the same trick again, forever: they show that the metatiles form clusters, and after a few steps the clusters from one step look the same as the clusters from the previous step, except bigger. These self-similar shapes are called supertiles. (Good job the proof ends after this step, because they’re running out of words for “bigger than”!)
Once you’ve identified the supertiles, you can perform a substitution to obtain the next step of the clustering process.
Remember that we’ve supposed you’re already looking at a complete tiling of the plane, and you’ve found a patch of adjacent supertiles. Replace each supertile with a certain arrangement of copies of the four possible supertiles, and the bigger patch of tiles you end up with must exactly match the tiling you’ve got, covering more of the plane than the patch you started looking at.
Because there’s no translation symmetry inside the supertiles, then there’s no translation symmetry among the metatiles, and hence the original tiles.
Reactions
The shape is really easy to make. I’ve created a GitHub repository of files representing the shape in various formats, for use in graphic design or 3D printing.
Dan Piker added some Truchet-like markings to the tile to make this nice pattern:
Dave Richeson was quick off the mark to print the tile on his 3D printer:
He’s put his model file on Thingiverse for anyone else who wants to print their own.
Travis Howse skipped a dimension and used his laser cutter to produce a set of tiles:
Adam Goucher has blogged about the paper, noting that the ratio of flipped tiles to unflipped tiles is $\phi^4$.
Dan Anderson has drawn the monotile using Mathigon’s interactive geometry tool, Polypad.
This meme by John May, who admits that it’s terrible, will not help with the einstein/Einstein confusion:

Read the paper
Really, read the paper! It’s very well-written, and deserves a lot of credit for going to extra lengths in the introduction to set the scene and provide the gist of the proof. If you just want to skim it, I suggest reading to the end of section 1.2 (“Outline”), and then the introductory paragraphs of each section after that. The subsections largely deal with the fiddly case-by-case checking that should be verified by somebody, but that needn’t be you.


Hi Christian, thank you for the nice write up, and for gathering some of the work people are putting together (so quickly!)
Best wishes,
Chaim
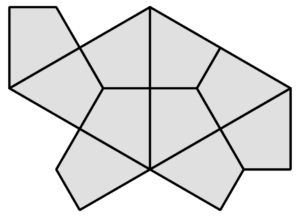
I hate to point to the repeats in the pattern but… (top left in main picture and to the right in the second one)
Beautiful shape though
Fixed! Thanks.
No
Great summary. Kudos for pointing out the difference between the possibility of an aperiodic tiling and the requirement of aperiodicity. Many other articles mix those up.
Full disclosure: I am not a qualified maths nerd.
But can somebody explain why a reflection of the tile counts as the same thing when we’re tiling a 2 dimensional plane? Feels like cheating to me.
Hi, Linda,
I’m not sure there’s a good answer to that. To a large degree, tiling is a game and we get to choose the rules together. If the game is too easy, we can make it harder. If it’s too hard, we can make it easier. I’m going to guess that people have tried to make an einstein that works without flipping and failed — maybe even proved it impossible? But I’m not sure about that. Does anyone else know?
Josh
The shapes are literally congruent. That’s the natural formalization of “same thing” in 2D.
If I want to tile the bathroom with this shape, I need two versions, hat and mirror image of hat? Does the same tile the other way up make a mirror image? Of course most bathroom tiles cannot be turned upside down, as the sides are finished differently.
Seems this need for mirror image tiles is a significant limitation that should be acknowledged in descriptions.
For the people asking this question, the 3-4-5 right triangle has two versions. Are there really two 3-4-5 right triangles? In 3-space they’re identical. In 2-space it’s a valid question. Euclid didn’t think they were different triangles.
If I create a jigsaw puzzle of the hat tiles, turquoise on top, blue on bottom, I don’t worry too much about whether the tile is turquoise or blue when I attempt to tile the plane.
Linda, I have the same concern as you. It would be valuable to learn from the authors on this point. I am unsure if the existence of a mirror-symmetric aperiodic monotile remains open, cannot happen, or is resolved by the work under review.
Thank you very much for publishing this. I have been waiting for a single tile aperiodic tiling pattern for fifty years!
@Linda. I agree it sounds like cheating, but if the pattern was in fact composed at the atomic or molecular level, flipping over an atom would be a legitimate operation in constructing a mono-layer. The fact that the ratio of flipped tiles to the rest is 1 to \(\phi^4\) (i.e. 1 to 6.854101966249685) is very significant. If this had been a periodic tiling, the ratio would have to be an integer, not an irrational number.
A monotile without reflection was discovered by the same authors later that year:
https://cs.uwaterloo.ca/~csk/spectre/
Good article – thank you for covering it so quickly.
Please remember that there is also a second polykite (the larger of the two) known as the turtle.
Can be update to wikipedia?
For clarity — Penrose tiles are the most famous (up to now at least…) but not the first — the first aperiodic set of tiles, by Robert Berger, had 20426 of them!
This is an amazing discovery, all the more so that the hat and turtle are just two members of an infinite family of shapes each of which is an aperiodic monotile. I note that you can trisect a regular hexagon (by 3 alternate apothems) into three pentagons each of which is two kites joined along long sides, and that the hat is four such pentagons, and the turtle is five of them. In a regular hexagon tiling there are two ways to trisect each hexagon (a Y and a Y turned 60 degrees); both hat and turtle force a mixture of the two ways. Perhaps this helps explain how come they can tile but not periodically?
It seems to me that they proved along the way that there are arbitrarily large sections that do have translational symmetry. So if those sections are not finite then who is to say that this is indeed aperiodic?
That’s exactly it: they proved those sections are always finite.
https://www.thingiverse.com/thing:5936513
Penrose aperiodic tilings have a global reflection symmetry about a unique line in the infinite plane. They also have a unique, esthetic, “radiative” center point on the line (although there is no rotational symmetry about it) I wonder if David Smiths tiling has these? I haven’t found anything yet upon searching. Haven’t scanned the paper yet though.
When Craig morphs the tiling by keeping angles but changing edge lengths, are there invariant points, that is, definable points on the hats which correspond to grid points in the underlying kite tiling?
I was so impressed by this discovery that I created a jigsaw puzzle game. Please come and play if you like.
https://store.steampowered.com/app/3550470/Infinite_Einstein_Tiles/