Since it’s $\tau$ Day, we thought we’d give Festival of the Spoken Nerd constant-fans Matt Parker and Steve Mould a chance to air their respective viewpoints in the $\tau$ vs $\pi$ debate. It’s a maths showdown!
You're reading: Features
Turing Round Up
Today is the 100th anniversary of Alan Turing’s birth. Turing did not just one but several hugely important things during his life, none of which were properly appreciated while he lived or for a long time after he died. In the run up to his centenary, a campaign to make people aware of Turing and the enormous impact he made on so many fields, and most importantly to clear his reputation, has been more successful than anyone could have hoped. Turing is now rightly recognised as one of the greatest mathematicians of the twentieth century, as a victim of persecution, and as a war hero.
The Turing Centenary campaign has been so successful that we’ve decided there’s no need for us to write a biography of Turing, or to highlight some obscure thing he did, or really anything. Literally hundreds of pieces have been written, by some of the greatest writers and thinkers in the world, covering every detail of Turing’s life from his school days to his more obscure mathematical work, up to the circumstances leading to his suicide.
So instead, we’ve collected together some of the best exposition, reporting, and creative expression we’ve found to commemorate the life of Alan Turing.
The Table Never Lies
The table never lies, or so they say. So when Manchester City were crowned Premier League Champions last week everyone seemed to agree that they were the best team in the league. As Roberto Mancini said, they had scored more than United and conceded less and beaten them twice in the league. Although United finished on the same number of points it would be difficult to find a measure by which they deserved the title over City. Or would it?
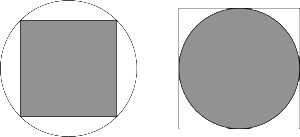
In what flipping dimension is a square peg in a round hole just as good as a round peg in a square hole?
In what flipping dimension is a square peg in a round hole just as good as a round peg in a square hole?
Let’s start at the beginning.
My Plus magazine puzzle from March asks “Which gives a tighter fit: a square peg in a round hole or a round peg in a square hole?” By “tighter” we mean that a higher proportion of the hole is occupied by the peg.
Grow Your Own Food
I recently heard about Herman, the German Friendship Cake (bear with me), a cake which is divided and spread among friends, and it got me thinking about some other foodstuffs I’ve heard of which are made in such a way that the amount you have will grow exponentially. A Herman cake is a special type of sourdough cake which is made with yeast. It’s explained fully here, but the idea is that you start with a solution of yeast, which lives in a little milk, sugar and flour. This small amount of goo can live happily at room temperature on a shelf, and if you stir it every day and give it a little more flour and sugar to eat every few days, after ten days it’s ready to make into a cake.
Klein: outside the bottle
 If you’ve heard of Felix Klein, it’s probably due to the Klein bottle, that strange four-dimensional object that is the subject of a new video here on The Aperiodical starring Katie Steckles and Matt Parker. Who is Klein and, apart from the bottle, what did he do?
If you’ve heard of Felix Klein, it’s probably due to the Klein bottle, that strange four-dimensional object that is the subject of a new video here on The Aperiodical starring Katie Steckles and Matt Parker. Who is Klein and, apart from the bottle, what did he do?
Klein’s Times obituary records that he would point out “with a smile” that his date of birth comprised three squares of primes. So then, I will refer to his birth as taking place on the $( 5^2 )^{\textrm{th}}$ day of the $(2^2 )^{\textrm{th}}$ month in the year $43^2$ in Prussia. You might like to notice that today is the $( 5^2)^{\textrm{th}}$ day of the $( 2^2 )^{\textrm{th}}$ month as well, so it is the 163rd anniversary of Klein’s birth.
Electoral reforms and non-transitive dice
Guest post by Andrew, of Manchester MathsJam. Andrew can be found on Twitter as @andrew_taylor and blogs occasionally about maths, among other things, at andrewt.net.
“Grime Dice” are a set of five coloured dice with unusual combinations of numbers on them. The red die, for example, has five fours and a nine. The blue one has three twos and three sevens, so it loses to the red die about 58% of the time. The green die has five fives and a zero, and will lose to the blue one in 58% of rolls. What makes them interesting is that the green die will beat the red one in 69% of rolls. These three dice behave rather like rock-paper-scissors — in mathematical terms, they are ‘non-transitive’. The full set of Grime Dice also has a purple and a yellow die, so a better analogy would be rock-paper-scissors-lizard-Spock.
