Benjamin Leis has been giving some top commentary on the Math-Off matches as they happen, on Twitter. We asked him to share some of his thoughts in more detail

We’re almost at the final of the Big Math-Off and I, your humble and slightly quirky commentator, thought I’d take a look back at the highlights so far. First of all, the format itself is genius. Why go to the beach when you could instead be rooting on for your favorite theorem or mathematical phenomenon? But if you somehow have missed any of the rounds so far, the posts live on and you should take the time to read them all.

Rather than exhaustively survey all the entries so far I thought I would highlight a few that struck a chord with me and what about them was interesting. So first up, since I’m involved in running a middle school math club, I’m always looking for ideas that will transfer to that setting. That generally means: ones only requiring inexpensive easy to procure materials, an idea that requires no more than Algebra and Geometry and which also has a good hook and most importantly, but which rules out a few otherwise excellent entries, it needs to be something that I haven’t done already.

For all the reasons mentioned I really liked Colin’s entry. It has a nice easy setup that I can easily see replicating at the school and doesn’t require much prior knowledge. There are several simplifications that can be tried out (less cards etc.) But after we get going, I can easily see branching out to some more advanced topics creating the networks of the potential relationships between cards and Hall’s Marriage Theorem. The only thing missing is convincing myself I have the simplest proof to aim for, at the end of the day. As another digression, it also reminds me of all the math inherent in the game Set that might make a good paired topic or a side activity for those kids who are near brain exhaustion.

The other project that I thought created fertile territory was Jim Propp’s appreciation of John Conway’s knot theory proof about knot cancellation. As an aside, if you haven’t played around with John Conway’s Rational Tangles: stop what you’re doing, check out the link and come back after being amazed. Again, this only take some strands of rope to get going and I can foresee a lot of physical experimentation. Unfortunately, I’m terrible at replicating feats of dexterity so I’d probably use the embedded videos directly at some point during the hour and focus my prep time on presenting the main proof. This would pair really well with another 3D topology topic or perhaps one of the many topological puzzles you can find at a game shop.

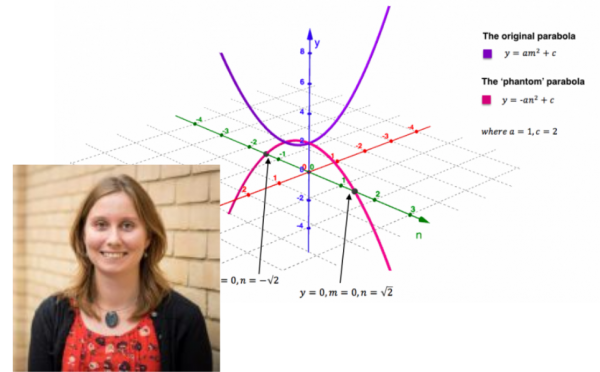
I’m also going to give an honorary mention here to Zoe Griffiths’ phantom parabolas.

While I’m not certain if I would use this in a group (while GeoGebra is a favorite of mine we lack enough computers) I did promise myself as soon as my rising Geometry student comes home from vacationing at his grandparent’s house to take a few minutes and share this with him. This is a fascinating visualization.

Moving onward to other categories, there were a few entries that made me say to myself “Wow that’s cool.”

For me, Matt Parker’s piece on Matthew Scrogg’s recreation of the MENACE tic-tac-toe machine learning experiment captured that special quality of childlike wonder. It’s a fun intersection between an incredibly simple setup (matchboxes and beads) and a rather profound topic: machine learning. Dynamic systems and subjects like neural nets are rarely so accessible.

Along the same lines I find all cellular automata fascinating and Nira Chamberlain’s explanation of Schelling’s model of segregation again makes me rue our lack of computers. Somehow I’m going to have to find a way to do these type simulations using just students and low cost physical objects.

Also despite being the only purely podcast entry, Samuel Hansen’s submission about Scott Feld’s finding the center of social networks through the second degree of connections was fascinating. It was new to me and I found myself taking out a pad, drawing some sample networks and exploring the phenomenon in action.

Finally I’d like to end with two topics that were familiar but featured presentations that were especially charming.

First, Alison Kiddle’s post on hat logic problems had one of the loveliest examples of camaraderie and the power of community among math lovers. The problem itself and exposition are great but then I reached the illustration above in the writing and I just stopped and smiled. I love that sense of connection she generates.

Likewise, despite having seen the math before James Tanton’s video exploring a classic Martin Gardneresque puzzle was amazing.

The combination of actually cutting cake rather than just drawing a figure and then re-icing it again after each step in a delightfully messy way was a ton of fun to watch.

So there you have it, a few of my favorite moments so far. I’m looking forward to the grand finale and am ready to be blown away by the last presentations. But more importantly, this has been a spot of unexpected fun and given me some inspiration for next Fall.

Benjamin Leis is a systems programmer by day and recreational mathematics lover by night who blogs at mymathclub.blogspot.com. You can also find him on Twitter as @benjamin_leis.